Непрерывность функции в точке и на промежутке

Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.

Функция 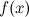называется непрерывной справа в точке , если .

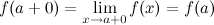Функция 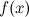называется непрерывной слева в точке , если .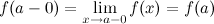

Функция 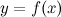называется непрерывной в интервале 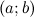, если она непрерывна в каждой точке этого интервала.

Функция 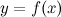называется непрерывной на отрезке 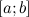, если она является непрерывной в интервале 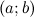, непрерывной справа в точке , то есть 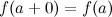и непрерывной слева в точке 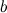, то есть .

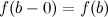Функция 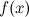называется непрерывной в точке , если:

1. функция 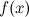определена в точке и ее окрестности;

2. существует конечный предел функции 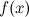в точке ;

3. это предел равен значению функции в точке , т.е.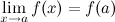

При нахождении предела функции 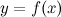, которая является непрерывной, можно переходить к пределу под знаком функции, то есть

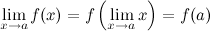
Задание. Вычислить предел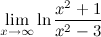

Решение.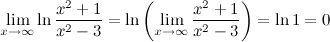

Ответ.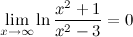

Асимптоты.

Аси́мпто́та(от греч. ασϋμπτωτος — несовпадающий, не касающийсякривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность

Виды асимптот:

Вертикальная

Вертикальная асимптота — прямая вида 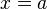при условии существования предела .

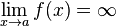Горизонтальная

Горизонтальная асимптота — прямая вида 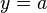при условии существования предела

.

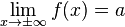Наклонная

Наклонная асимптота — прямая вида 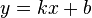при условии существования пределов

Порядок нахождения асимптот

1. Нахождение вертикальных асимптот.

2. Нахождение двух пределов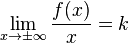

3. Нахождение двух пределов :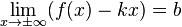

если 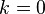в п. 2.), то 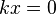, и предел 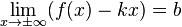находится по формуле горизонтальной асимптоты, .

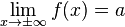Понятие производной. Основные правила дифференцирования.

Произво́дная (функции в точке) — основноепонятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.

Таблица производных

Производные степенных функций	Производные тригонометрических функций	Производные обратных тригонометрических функций

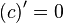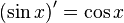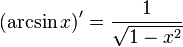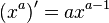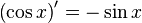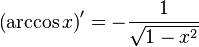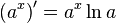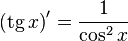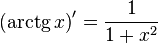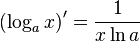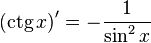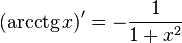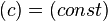
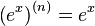
Правила дифференцирования

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

·

·

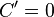
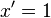
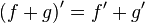· ^[2]

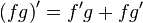· ^[3]

·

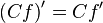
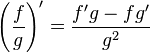· …(g ≠ 0)

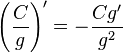· (g ≠ 0)

· Если функция задана параметрически:

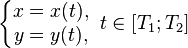, то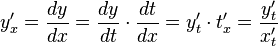

Основная статья: Дифференцирование сложной функции

·

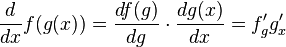
· Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):

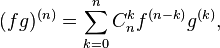где 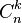— биномиальные коэффициенты.

Следующие свойства производной служат дополнением к правилам дифференцирования:

· если функция дифференцируема на интервале 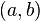, то она непрерывна на интервале 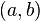. Обратное, вообще говоря, неверно (например, функция 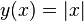на );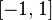

· если функция имеет локальный максимум/минимум при значении аргумента, равном 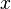, то 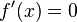(это так называемая лемма Ферма);

· производная данной функции единственна, но у разных функций могут быть одинаковые производные.

·

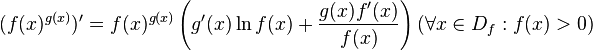
Доказательство

■
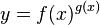
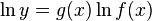
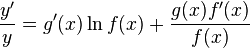
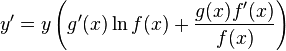
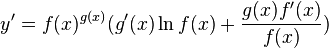