Нормальное распределение непрерывной случайной величины

К случайным величинам, имеющим нормальный закон распределения, относятся случайные величины, на формирование которых влияет большое число факторов, причем влияние каждого из них мало и ни один фактор не имеет значительного преимущества перед другими. В результате влияния каждого из этих факторов рождается ничтожная случайная ошибка. Поскольку число этих факторов велико, то совокупное их действие порождает суммарную ошибку. Эту суммарную ошибку можно рассматривать как сумму большого числа взаимно независимых ошибок, т.е. суммарную ошибку можно рассматривать как случайную величину, которая распределена по закону, близкому к нормальному.

Определение 16.1. Случайная величина подчиняется нормальному закону распределения, если ее функция плотности вероятностей имеет вид

,

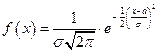где 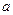и s - параметры распределения.

Методами интегрального исчисления можно проверить, что эта функция удовлетворяет следующим условиям:

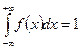, (16.1)

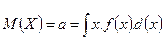, (16.2)

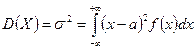. (16.3)

Значит, параметр 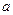- есть математическое ожидание данной случайной величины , т.е. центр рассеяния случайной величины распределенной нормально, а параметр s - есть её среднее квадратическое отклонение, которыми полностью определяют нормальное распределение.

А величина 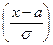есть нормированная случайная величина, у которой

; .

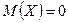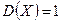Определение 16.2. График функции 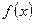называется кривой нормального распределения, это колоколообразная кривая или кривая Гаусса.

Методами дифференциального исчисления можно исследовать функцию

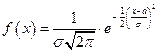
и установить, что: 1) О.О.Ф.: 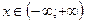; 2) О.И.Ф.: 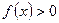, т.е. график расположен выше оси абсцисс; 3) 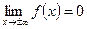, т.е. ось абсцисс есть горизонтальная асимптота графика функции; 4) 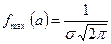, то есть точка максимума имеет координаты 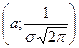; 5) точки перегиба графика функци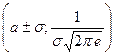и или ;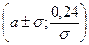
6) кривая, симметричная относительно прямой (рис. 16.1).

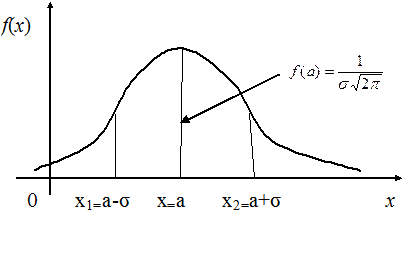
Рис. 16.1

Влияние параметров распределения а и s на форму нормальной кривой.Изменение величины параметра 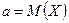не изменяет формы кривой, а только сдвигает её вдоль оси 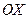вправо, если 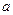возрастает, и влево, если 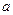убывает, при неизмененном значении s (рис. 16.2).

Рис. 16.2

Форма кривой изменяется с изменением параметра s - среднего квадратического отклонения. С возрастанием s ордината максимума функции 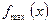уменьшается, т.е. 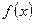убывает и кривая становится более пологой и растянутой вдоль оси 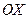. Чем ближе значения 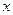к 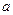, тем больше плотность вероятности 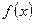с уменьшением s, т.е. максимальная ордината функции возрастает, и график функции 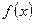сжимается к прямой 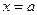параллельной 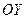, т.е. растягивается вдоль прямой 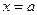параллельной 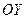, т.е. кривая становится более «островершинной». Малые отклонения случайной величины от её среднего значения встречаются более часто, чем большие; а S – площадь фигуры, ограниченной кривой 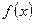и осью , всегда равна 1.

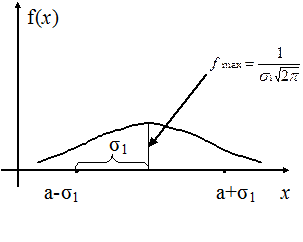
Рис. 16.3 Рис. 16.4

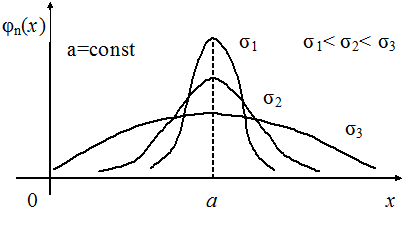
Рис. 16.5

Определение 16.3. Если 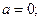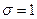, то нормальное распределение называется нормированным и функция плотности или дифференциальная функция имеет вид

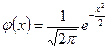
– это функция Лапласа (рис. 16.6).

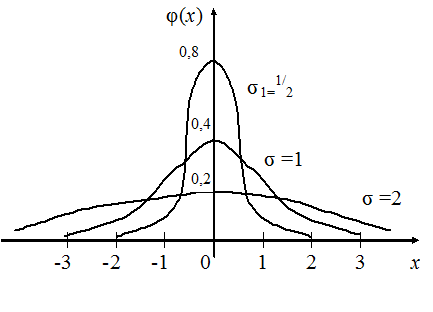
Рис. 16.6

Нормальное распределение имеет в теории вероятностей большое значение, так как оно рассматривается как приближение многих других распределений. Так, биномиальное распределение близко к нормальному при 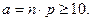. Распределение Пуассона близко к нормальному распределению, когда 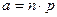- достаточно велико, т.е. 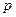- мало, а 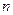- велико.

Пример 16.1. Случайная величина распределена нормально. 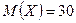; 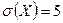. Написать дифференциальный закон распределения случайной величины.

; .

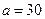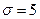
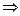
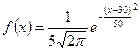Пример 16.2. Дифференциальная функция распределения случайной величины имеет вид

.

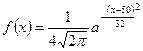Найти параметры заданного распределения.

Ответ: ; .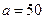

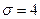Вероятность попадания случайной величины, распределенной по нормальному закону, в интервал (a; b).Известна формула, которая позволяет рассчитать вероятность попадания значений случайной величины непрерывного типа в заданный интервал (a; b):

,

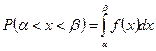где 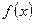- заданная дифференциальная функция распределения, характеризующая величину ; a - левая; b - правая границы заданного интервала. Для нормального распределения случайной величины имеем

.

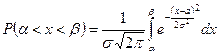Методами интегрального исчисления можно получить формулу

.

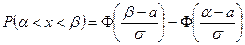Графически эта вероятность равна площади криволинейной трапеции, ограниченной нормальной кривой, прямыми 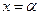; 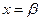и осью .

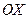Пример 16.3. Случайная величина распределена нормально с 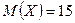и 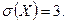Найти вероятность того, что примет значение из интервала (10; 25).

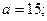
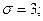
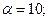
Легко видеть, что 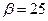и тогда

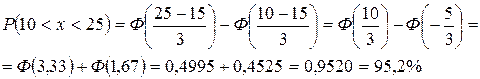
Ответ. С вероятностью 95,2% можно ожидать, что случайная величина , распределенная нормально, примет любое значение из интервала (10; 25).

Пример 16.4. Средний диаметр стволов деревьев на обследуемом участке равен 30 см; среднее квадратическое отклонение - 5 см. Считая, что диаметр ствола - величина случайная, распределенная нормально, определить вероятность того, что:

1) диаметр ствола наугад выбранного, дерева попадает в интервал (25 см; 37 см);

2) диаметр ствола будет не менее 25 см;

3) диаметр ствола дерева не превысит 36 см;

4) определить величину, которую не превзойдет диаметр ствола наугад выбранного дерева с вероятностью 0,95.

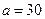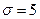Случайная величина - диаметр ствола дерева распределена нормально; см; см.

1)

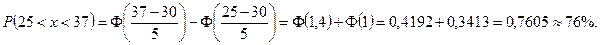
Это значит, что 76% стволов деревьев имеют диаметры от 25 до 37 см.

2) Событие, состоящее в том, что диаметр ствола дерева будет не менее 25 см, определяется неравенством 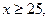значит надо найти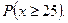

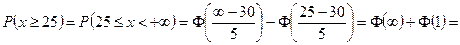
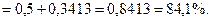
3) Событие состоящее в том, что диаметр ствола дерева будет не более 36 см, определяется неравенством 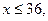а значит:

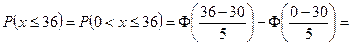
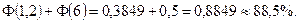
Итак, 84,1% стволов деревьев на участке будут иметь диаметры не менее 25 см и 88,5% - не более 36 см.

4) Надо найти правую границу b по заданной вероятности 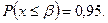Левую границу принимаем равной 0.

;

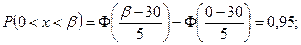
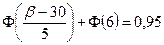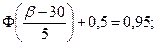
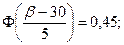
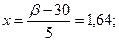
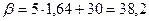(см).

Таким образом, диаметр ствола выбранного наугад дерева на некотором участке, не будет превышать 38,2 см с вероятностью 0,95, или 95% деревьев на участке будут иметь диаметры не более 38,2 см.

Вероятность попадания случайной величины, распределенной нормально, в интервал, симметричный относительно центра рассеяния. Надо найти вероятность неравенства 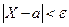, где - величина, распределенная нормально, 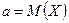; e - любое положительное число.

.

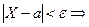
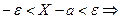
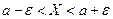Если то имеет место (рис. 16.7).

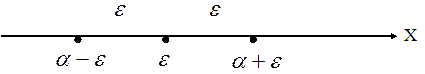
Рис. 16.7

В результате вычислений получим формулу:

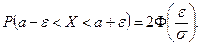
Пример 16.5. Длина детали, изготовляемой в цехе, представляет собой случайную величину, распределенную нормально с 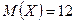мм и 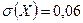мм. Найти: 1) вероятность того, что длина готовой детали отклоняется от номинального размера не более чем на 0,02 мм; 2) какую точность изготовления длины детали можно ожидать с вероятностью 0,99?

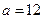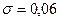Случайная величина мм - длина детали, распределенная нормально: мм; 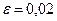мм; мм.

1) Найдём

.

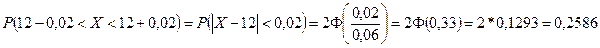Значит, примерно 26% деталей имеют длину 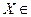(11,98; 12,02) мм.

С увеличением величины отклонения e , т.е. с понижением точности изготовления детали, возрастает вероятность осуществления неравенства .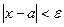

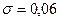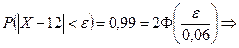
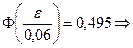
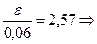
2) По условию задачи мм, поэтому 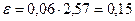(мм).

Ответ. Примерно 99% деталей имеют длину 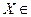(11,85; 12,15) мм. Как и следовало ожидать, с увеличением вероятности отклонения 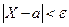величина отклонения возросла, что привело к снижению точности изготовления детали.

Правило трёх сигм.В формуле

,

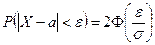полагаем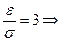

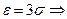
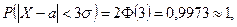
т.к.

.

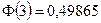Определение 16.4. Вероятность того, что отклонение случайной величины от 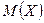по абсолютной величине не превысит 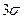, близка к 1 (рис. 6), т.е. неравенство 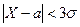практически достоверно.

Это значит, что случайная величина, распределенная нормально, практически не может отклониться от своего математического ожидания более чем на три средних квадратических отклонения. На практике при испытаниях значения с.в. , распределенной нормально, будут принадлежать интервалу 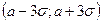с вероятностью, близкой к единице (рис. 16.8, 16.9). В самом деле,

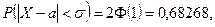
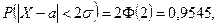
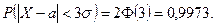
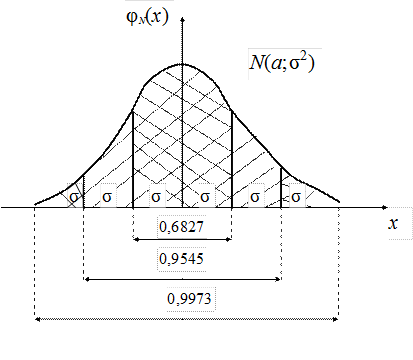
Рис. 16.8

Правило трех сигм, например, может быть применено в статистическом контроле качества изделий.

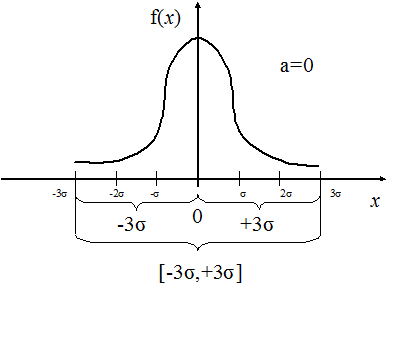
Рис. 16.9