Множина дійсних чисел R, її властивості. Поняття верхньої і нижньої граней числової множин, їх існування і властивості. Теорема Кантора
Аналіз поняття множини. Потужність множини. Зчисленні множини та їх властивості. Множини натуральних чисел N, цілих Z, раціональних Q, та дійсних чисел R, їх потужність.
Поняття множини належить до первісних понять, воно не визначається. Під множиною розуміємо сукупність, зібрання деяких об’єктів, які мають певну характеристичну властивість. Напри. А= 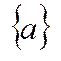 , a є А.
, a є А.
В результаті лічби, переліку виникли натуральні числа 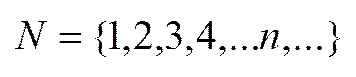
Властивості натуральних чисел: 1)переставна властивість додавання, або комунікативність a+b=b+a; 2) сполучна властивість додавання, або асоціативність (a+b)+c=a+(b+c); 3) переставна властивість множення ab=ba; 4) сполучна властивість множення (ab)c=a(bc); 5) розподільна властивість множення відносно додавання, або дистрибутивність a(b+c)=ab+ac. Натуральне число, крім 1, називається простим, якщо воно ділиться на одиницю і само на себе. Прості числа: 2, 3, 5, 7, 11, 13, 17.
Множину цілих чисел утворюють натуральні числа, їм протилежні, а також число 0. 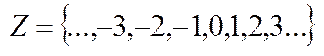 . Цілі числа мають ті ж самі властивості, що й натуральні числа.
. Цілі числа мають ті ж самі властивості, що й натуральні числа.
Множину раціональних чисел утворюють цілі і дробові числа. Познач. Q. Будь-яке раціональне число можна записати у вигляді 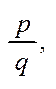 де р є Z, q є N. Власт.: а) множина Q впорядкована
де р є Z, q є N. Власт.: а) множина Q впорядкована 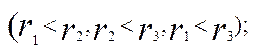 б) множина Q щільна в собі; в) а і в-раціон., то сума, різниця, добуток – раціон; г) кожне Q число на прямій лінії може бути зображено як певна точка цієї прямої.
б) множина Q щільна в собі; в) а і в-раціон., то сума, різниця, добуток – раціон; г) кожне Q число на прямій лінії може бути зображено як певна точка цієї прямої.
Числа раціон. і нераціон. утворюють множину дійсних чисел. Позн. R N<Z<Q<R Кожна з них включає наступну.
Власт:
1) множина дійсних чисел впорядкована 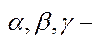 дійсні числа
дійсні числа 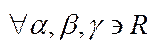
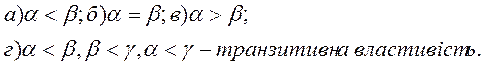
2)властивість операцій додавання: а) для будь-якого впорядкованого 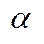 і
і 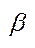 є число
є число 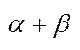 ; б) для будь-якого впорядкованого числа є існує сума
; б) для будь-якого впорядкованого числа є існує сума 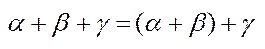 ; в)
; в) 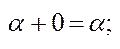 г)
г) 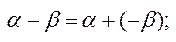
3) властивості операцій множення 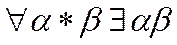 ;
;
4) Зв’язок операцій додав. і множення: а) розподільний закон; б) 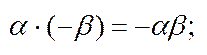
5) Множина дійсних чисел дійсна 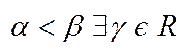 :
: 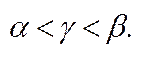
6) Властивість неперервних дійсних чисел. Множина всіх R-чисел на інтервалі 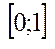 незлічена
незлічена
Множина елементів, які задовольняють влас. 1-6 назив. множиною дійсних чисел, а кожен елемент цієї множини назив. дійсним числом.
Множина дійсних чисел R, її властивості. Поняття верхньої і нижньої граней числової множин, їх існування і властивості. Теорема Кантора.
Числа раціон. і нераціон. утворюють множину дійсних чисел. Позн.R N<Z<Q<R Кожна з них включає наступну.
Власт:
1) множина дійсних чисел впорядкована 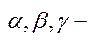 дійсні числа
дійсні числа 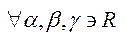
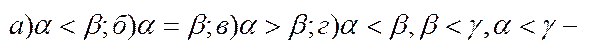 транзитивна властивість;
транзитивна властивість;
2)властивість операцій додавання: а) для будь-якого впорядкованого 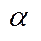 і
і 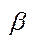 є число
є число 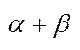 ; б) для будь-якого впорядкованого числа є існує сума
; б) для будь-якого впорядкованого числа є існує сума 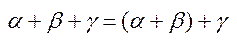 ; в)
; в) 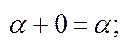 г)
г) 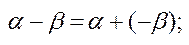
3) властивості операцій множення 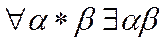 ;
;
4) Зв’язок операцій додав. і множення: а) розподільний закон; б) 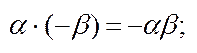
5) Множина дійсних чисел дійсна 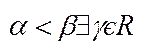 :
: 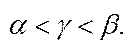
6) Властивість неперервних дійсних чисел. Множина всіх R-чисел на інтервалі 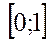 незлічена .
незлічена .
Множина елементів, які задовольняють влас. 1-6 назив. множиною дійсних чисел, а кожен елемент цієї множини назив. дійсним числом.
Нехай a i b - дійсні числа( 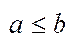 ), тоді сукупність чисел х, що задовольняють нерівність
), тоді сукупність чисел х, що задовольняють нерівність 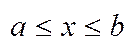 назив. числовим відрізком, або сегментом і позначаються
назив. числовим відрізком, або сегментом і позначаються 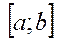 , a i b права, ліва межі. Якщо a=b, то відрізок містить тільки одну точку. Число b-a називається довжиною відрізка
, a i b права, ліва межі. Якщо a=b, то відрізок містить тільки одну точку. Число b-a називається довжиною відрізка 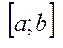 . Система числових відрізків
. Система числових відрізків 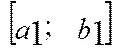 ,
, 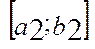 ,…,
,…, 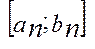
 називається системою вкладених відрізків. Якщо
називається системою вкладених відрізків. Якщо 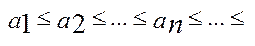
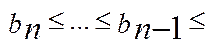
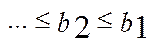 .
.
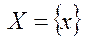 , x є R .Числова множина X називається обмеженою, якщо існує такі числа m, M є R:
, x є R .Числова множина X називається обмеженою, якщо існує такі числа m, M є R: 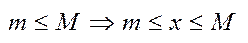 ,
, 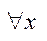 є Х.Числа m і M називаються відповідно нижньою і верхньою межами.
є Х.Числа m і M називаються відповідно нижньою і верхньою межами.
Визначення 1. Найменша з усіх верхніх меж обмежених зверху числової множини називається точною верхньою межею (гранню).І познач 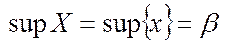 .
.
Визначення 2.Найбільша з усіх нижніх меж обмеженою знизу числової множини називається точною нижньою межею(гранню). І позначається 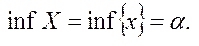 Точні нижні і верхні межі можуть як належати так і не належати даній множині.
Точні нижні і верхні межі можуть як належати так і не належати даній множині.
Властивості точних нижньої і верхньої множини:
1. х є 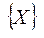
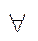 х є Х
х є Х 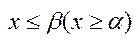 .
.
2. 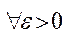
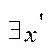 є Х ;
є Х ; 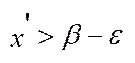 (
( 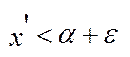 ).
).
Теорем Кантора. Для будь-якої системи вкладених відрізків існує хоча б одне число, яке належить усім відрізкам даної системи цю властивість дійсних чисел називають неперервність множин дійсних чисел .
Теорема. Всяка непорожня числова множина з елементами x обмежена зверху (знизу) має точну верхню (нижню) межу.
Доведення. Доведемо для верхньої межи. Нехай х є Х- не порожня обмежена зверху, тоді існує хоча б один елемент х є Х, цієї множини і існує таке число b, що для всіх х справджується нерівність 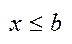 , тому відрізок
, тому відрізок 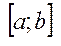 містить хоча б один елемент множини х. Треба показати, що для елемент
містить хоча б один елемент множини х. Треба показати, що для елемент 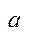 задовольняють 1-2 влас. точної верхньої межі. Ділимо відрізок
задовольняють 1-2 влас. точної верхньої межі. Ділимо відрізок 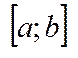 пополам, одержимо два відрізки, одержимо
пополам, одержимо два відрізки, одержимо 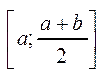 ,
, 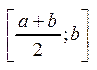 . В одній із половин половина містить одне число чи точкою множини. Позначимо відрізки через
. В одній із половин половина містить одне число чи точкою множини. Позначимо відрізки через 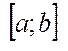 пополам і виберемо з них в якому міститься, хоч одна точка множини Х і так далі
пополам і виберемо з них в якому міститься, хоч одна точка множини Х і так далі 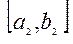 , …
, … 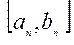 . Одержимо систему вкладених відрізків.
. Одержимо систему вкладених відрізків.
Довжина 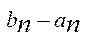 буде дорівнювати
буде дорівнювати 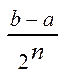 =0,
=0, 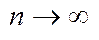 . Точка в яку стягується система вкладених відрізків позначимо
. Точка в яку стягується система вкладених відрізків позначимо 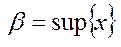 . Для того, щоб показати що число
. Для того, щоб показати що число 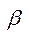 задовольняє 1-2 власт. Доведення методом від супротивного: припустимо, щоіснує елемент
задовольняє 1-2 власт. Доведення методом від супротивного: припустимо, щоіснує елемент 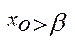 , тоді оскільки довжина проміжка
, тоді оскільки довжина проміжка 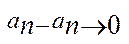 , то існує таке
, то існує таке 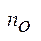 , що
, що 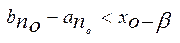 .З цієї нерівності випливає, що
.З цієї нерівності випливає, що 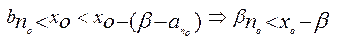 . Але для всіх х є Х виконується нерівність
. Але для всіх х є Х виконується нерівність 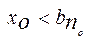 . Отже, не існує таке число, що
. Отже, не існує таке число, що 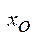 є Х,
є Х, 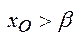 . Покажемо
. Покажемо 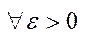
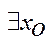 є Х;
є Х; 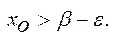 Виберемо такий номер
Виберемо такий номер 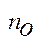 , що виконується нерівність
, що виконується нерівність 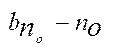 Отже, для всіх
Отже, для всіх 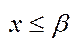 виконується нерівність
виконується нерівність 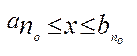 ,
, 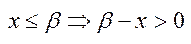 , або
, або 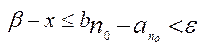 . Звідси випливає, що
. Звідси випливає, що 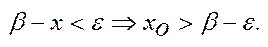
Доведення (другу частина). Для доведення існування точної нижньої межі поступають так. Нехай m- нижня межа, покажемо 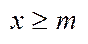 , що
, що 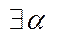 , помножимо на -1,
, помножимо на -1, 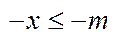 . Тоді
. Тоді 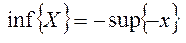 отримаємо
отримаємо 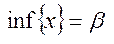 , будуть задовольнятись 1,2-власт, тоді замість х ставить –х,
, будуть задовольнятись 1,2-власт, тоді замість х ставить –х, 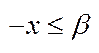 1 домножимо на -1ажемо ї межі поступають так.
1 домножимо на -1ажемо ї межі поступають так.
