Основные свойства объектов регулирования

На процесс регулирования физических параметров оказывают влияние как свойства регулирующей части системы (регулятора), так и свойства объекта регулирования. Как правило, перед созданием системы тщательно изучают объект регулирования. Определяют статические и динамические характеристики объекта и на их основе формулируют требования к регулятору системы.

Основными свойствами объекта регулирования являются:

– емкость объекта (коэффициент емкости объекта);

– самовыравнивание;

– время разгона и скорость разгона;

– запаздывание.

Под емкостью регулируемого объекта подразумевается его способность накапливать энергию или вещество. Если объект регулирования обладает малой емкостью, то регулируемый параметр изменяется быстро и наоборот. Чем больше емкость объекта, тем проще решается задача регулирования. Например, при регулировании относительной влажности в помещениях последняя изменяется значительно быстрее, чем температура. Это означает, что помещения обладают существенно меньшей емкостью при регулировании влажности, чем температуры. Отсюда следует, что поддерживать относительную влажность в помещениях более сложно, чем температуру.

Емкость объекта регулирования чаще всего определяют экспериментальным путем, в связи, с чем имеющиеся аналитические зависимости можно применять в ограниченных случаях.

Самовыравниванием называется свойство регулируемого объекта после нарушения равновесия в объекте под действием возмущения вернуться к этому состоянию самостоятельно, без участия человека или регулятора.

Предположим, что уровень жидкости L₀ в резервуаре (рис. 3.6а) постоянный, то есть имеет место баланс F_п = F_р.

Если открыть клапан 1, то приток F_п увеличится (рис. 3.6б). Уровень жидкости L возрастает, что приводит к увеличению гидростатического напора жидкости в резервуаре и, следовательно, расхода F_р жидкости. При определенном новом уровне L₁ опять будет выполняться равенство F_п = F_р. Таким образом, рассмотренный объект обладает самовыравниванием (рис. 3.6с). При откачивании жидкости из резервуара насосом данный объект теряет свойство самовыравнивания (рис. 3.6д).

Рис. 3.6. Переходный процесс в объектах с самовыравнива-

нием (с) и без самовыравнивания (д)

Количественная оценка объектов регулирования с точки зрения самовыравнивания характеризуется коэффициентом (степенью) самовыравнивания . На практике степень самовыравнивания объектов регулирования определяют с помощью кривых самовыравнивания (разгона) объектов, полученных экспериментальным путем.

Для примера на рис. 3.7 представлена кривая разгона теплового объекта (например, ПК + помещение), по которой можно определить основные характеристики объекта. По кривой разгона определяют полное запаздывание объекта 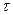, постоянную времени Т и коэффициент передачи (усиления) объекта К.

Если в точке А, соответствующей максимальной скорости изменения выходной величины (температуры), провести касательную к кривой разгона и продолжить ее до пересечения с линиями начального (т. В) и конечного (т. С) установившихся значений температуры, тоотрезок ОВ соответствует полному запаздыванию 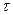, а отрезок ВЕ – постоянной времени объекта Т. Величина Т показывает время, за которое выходная величина достигнет нового установившегося значения при сохранении ее максимальной скорости изменения.

Рис. 3.7. Кривая разгона теплового объекта: – увеличение теплоотдачи воздухонагревателя в относительных единицах; – увеличение температуры воздуха в помещении в относительных единицах

Коэффициент передачи объекта

,

где и принимаются в относительных единицах.

Самовыравнивание способствует более быстрой стабилизации регулируемой величины, что облегчает работу регулятора.

Следует заметить, что большинство объектов в системах ТГиВ обладают самовыравниванием.

Временем разгона объекта называется промежуток времени, который бы потребовался для достижения объектом полной нагрузки при сообщении ему максимального возмущающего воздействия. Например, время опорожнения или наполнения резервуара с водой при постоянной скорости, когда возмущающее воздействие максимальное.

Величину можно определить с помощью кривой разгона из соотношения

, где .

Скоростью разгона называется величина, обратная времени разгона

.

Объектам систем ТГиВ характерны незначительные возмущения, при которых имеют место небольшие скорости изменения регулируемого параметра (температуры, расхода, давления, уровня и др.). С точки зрения автоматического регулирования – это является их положительным свойством.

Запаздывание процесса регулирования 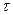– это время от момента приложения воздействия до того момента, когда регулируемый параметр начнет изменяться. Различают емкостное и чистое (транспортное) запаздывание.

Емкостное запаздывание зависит от емкости объекта и наблюдается в многоемкостных объектах. Например, любой теплообменный аппарат является двухемкостным объектом.

Чистым запаздыванием называется промежуток времени, после которого действие регулирующего воздействия начнет сказываться на регулируемом объекте.

Сумма чистого и емкостного запаздывания составляет полное запаздывание 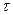. Эту величину можно определить по кривой разгона объекта регулирования.

Чем больше время полного запаздывания 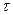, тем труднее регулировать параметры технологического процесса. Поэтому в многоемкостных объектах необходимо путем применения специальных мер стремиться к уменьшению величины 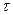. Например, в теплообменных аппаратах необходимо предусматривать минимально возможную толщину стенок воздухонагревателей, водоподогревателей и изготавливать их из малотеплоемких металлов, имеющих значительные коэффициенты теплопроводности. Кроме того, необходимо, чтобы количество греющей воды в теплообменном аппарате на стороне подачи было также минимальным.

Динамические звенья САР

В процессе работы САР может находиться в статическом или динамическом режиме. Наиболее сложным и важным для САР является динамический режим, когда происходит перемещение регулирующего органа и изменение регулируемого параметра объекта (см. рис. 3.1).

Динамические процессы САР описываются дифференциальными уравнениями, с помощью которых удается провести количественный анализ системы регулирования. Обычно дифференциальные уравнения систем регулирования имеют высокий порядок (4-й, 5-й и более), поэтому всю систему регулирования разделяют на сравнительно простые части (динамические звенья) и с помощью уравнений этих частей не более 2-го порядка составляют дифференциальное уравнение всей системы регулирования.

Динамическим звеном называется часть системы регулирования, описываемая дифференциальным или иным уравнением определенного типа. Отличие элемента от динамического звена состоит в том, что элемент может состоять из нескольких динамических звеньев. Для динамического звена не является обязательным конструктивное или схемное оформление. В отдельных случаях динамическое звено может вообще не иметь физического смысла, характеризуя лишь математические зависимости между некоторыми величинами автоматической системы.

Условное изображение динамического звена представлено на рис. 3.8, где 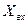, 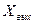– входная и выходная величины звена, f – возмущающее воздействие.

В общем случае обе величины 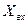и 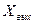представляют собой функции времени.

Рис. 3.8

Статической характеристикой звена называется зависимость выходного сигнала 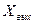от входного сигнала 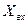в установившемся режиме, то есть

.

По виду статических характеристик все элементы (звенья) автоматических систем делятся на линейные и нелинейные звенья. Статическая характеристика линейного звена имеет вид прямой линии (рис. 3.9а)

,

где k – коэффициент передачи звена (или усиления звена).

Обычно статические характеристики элементов и звеньев автоматических устройств нелинейные (см. рис. 3.9 б, в, г). Однако в инженерной практике часто нелинейные характеристики приближенно заменяются линейными (рис. 3.9в). Такое приближение называется линеаризацией.

Рис. 3.9. Статические характеристики звеньев

Статическая характеристика полностью характеризует поведение динамического звена в установившихся режимах.

Динамические характеристики выражают зависимость выходной величины от входной в динамическом (переходном) режиме, когда обе эти величины изменяются во времени. Динамические свойства звеньев описываются дифференциальными уравнениями, связывающими входную и выходную величины звеньев во времени.

Например, большинство тепловых объектов описываются дифференциальным уравнением

, (3.1)

где 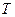– постоянная времени объекта, с; К – коэффициент усиления объекта.

Часто дифференциальные уравнения записывают в операторной форме. Для этого символ дифференцирования заменяют операторным символом :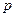

; . (3.2)

Соответственно для операции интегрирования вводятся обратные обозначения

; и т.д. (3.3)

Замена в дифференциальных уравнениях позволяют получить выражения, формально совпадающие с выражениями изображений по Лапласу.

В операторной форме записанное дифференциальное уравнение (3.1) будет иметь вид

(3.4)

или

. (3.5)

Символ 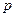можно рассматривать как обычный множитель и производить над ним все математические преобразования: выносить за скобку, сокращать и т.п. Операторная форма обозначения сокращает объем записи, упрощает промежуточные математические выражения при анализе систем регулирования.

Общее и полное выражение динамических и статических свойств звена дается его передаточной функцией.

Передаточная функция – это отношение, записанных в операторной форме, выходной величины звена к входной при нулевых начальных условиях

.(3.6)

Передаточную функцию теплового объекта можно получить из операторного уравнения (3.5)

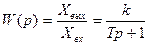,(3.7)

где К – коэффициент усиления, характеризующий статические свойства объекта; Т – постоянная времени, характеризующая динамические свойства объекта.

Любое исследование звена (объекта) в конечном счете, сводится к определению его передаточной функции.

Частотные характеристики звеньев. В реальных системах часто входные сигналы звеньев или систем изменяются по гармоническому закону заданной амплитуды и частоты. В таких случаях параметры колебаний на выходе звена с помощью переходной характеристики получить трудно. В тоже время частотный метод позволяет получить выходные параметры звена при любом входном периодическом сигнале.

При подаче на вход звена гармонического сигнала

(3.8)

получаем на выходе звена сигнал

, (3.9)

где A и B – амплитуды входного и выходного сигналов; – угловая частота; T – период колебаний; – фазовый сдвиг между входными и выходными колебаниями.

Выражения (3.8) и (3.9) можно представить в виде графиков (рис. 3.10)

Рис. 3.10.

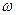При значении амплитуда B и фаза зависят от частоты . Если постепенно увеличивать от нуля 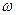, определяя установившиеся значения B и для разных частот при фиксированном значении А, то можно получить зависимости

и , (3.10)

где – амплитудно-частотная характеристика; – фазовая частотная характеристика.

Синусоидальные величины 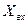и 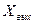(рис. 3.10) можно представить в виде вращающихся векторов на комплексной плоскости (рис. 3.11).

Вращающийся вектор синусоидальной величины можно представить на комплексной плоскости комплексным числом, представленным в показательной, тригонометрической и алгебраической форме. Переход от одной формы записи к другой осуществляется с помощью формулы Эйлера

. (3.11)

Тогда 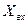и 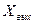можно представить в виде (3.12)

Рис. 3.11

При определении передаточной функции воспользуемся комплексными числами векторов и , записанными в показательной форме. При этом сделаем замену . Тогда

, (3.13)

а так как величины и зависят от 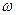(при А = const), то час-

тотная передаточная функция будет иметь вид (3.14)

где – вещественная частотная характеристика; – мнимая частотная характеристика.

Таким образом, подставляя в выражение для передаточной функции в место 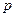комплексную величину 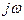, можно получить однозначную зависимость между передаточной функцией и частотными характеристиками звена. Величина называется амплитудно-фазовой частотной характеристикой (АФЧХ).

Частотные характеристики позволяют сократить объем вычислительной работы при анализе САР и нашли широкое применение на практике при оценке устойчивости и качества систем регулирования.