Порівняння нескінченно малих
якщо f(x) і j(x) – нескінченно малі при x®а, причому а може бути як числом, так одним із символів 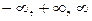 , тоді справедливі наступні визначення.
, тоді справедливі наступні визначення.
Якщо 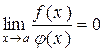 , то f(x) називається нескінченномалою вищого порядку малості, у порівнянні з функцією j(x), а функція j(x) називається нескінченномалою нижчого порядку малості, у порівнянні з f(x). , то f(x) називається нескінченномалою вищого порядку малості, у порівнянні з функцією j(x), а функція j(x) називається нескінченномалою нижчого порядку малості, у порівнянні з f(x). |
Якщо 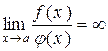 , то f(x) називається нескінченно малою нижчого порядку малості, у порівнянні з j(x), а j(x) називається нескінченномалою вищого порядку малості, у порівнянні з функцією f(x). , то f(x) називається нескінченно малою нижчого порядку малості, у порівнянні з j(x), а j(x) називається нескінченномалою вищого порядку малості, у порівнянні з функцією f(x). |
Якщо 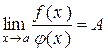 і і 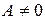 , то нескінченно малі f(x) і j(x) називаються нескінченномалими одного порядку. , то нескінченно малі f(x) і j(x) називаються нескінченномалими одного порядку. |
Якщо 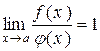 , то нескінченно малі f(x) і j(x) називаються еквівалентними.Позначення f(x) ~ j(x). , то нескінченно малі f(x) і j(x) називаються еквівалентними.Позначення f(x) ~ j(x). |
Якщо 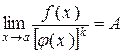 і і 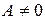 , то f(x) називається нескінченномалою k-го порядку малості, у порівнянні з j(x). , то f(x) називається нескінченномалою k-го порядку малості, у порівнянні з j(x). |
| Границя відношення двох нескінченно малих не зміниться, якщо кожну з них або яку-небудь одну замінити еквівалентними ним. |
При обчисленні границь функцій зручно користатися такими основними еквівалентностями.
Основні еквівалентності при 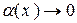
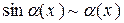 ,
, 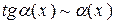 ,
, 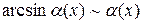 ,
, 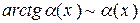 ,
,
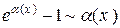 ,
, 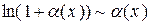 ,
, 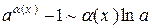 .
.
Приклад 2.17.Довести, що функції 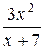 і
і 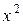 при x ® 0 є нескінченно малими одного порядку.
при x ® 0 є нескінченно малими одного порядку.
Розв’язання.Знайдемо границю відношення заданих функцій:
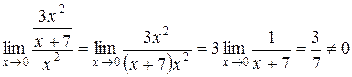 .
.
Таким чином, дані функції є нескінченно малими одного порядку.
Приклад 2.18.Чи єеквівалентними функції 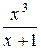 і
і 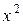 при x ® 0?
при x ® 0?
Розв’язання.Знайдемо границю відношення цих функцій:
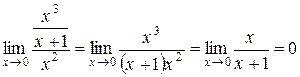 .
.
Таким чином, функція 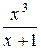 є нескінченно малою більш високого порядку, ніж функція
є нескінченно малою більш високого порядку, ніж функція 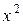 , тобто дані функції не еквівалентні.
, тобто дані функції не еквівалентні.
Приклад 2.19.Довести,щонескінченно малі функції 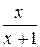 і
і 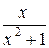 при x®0 є еквівалентними.
при x®0 є еквівалентними.
Розв’язання.Очевидно, що 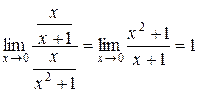 . Отже,
. Отже, 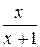 і
і 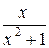 при x ® 0 еквівалентні.
при x ® 0 еквівалентні.
Визначні границі
Перша визначна границя.
При обчисленні границь тригонометричних виразів часто використовують формулу
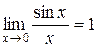 . (2.5)
. (2.5)
Формула (2.5) називається першою визначною границею і застосовується для розкриття невизначеностей виду 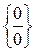 .
.
Справедливі наступні відношення:
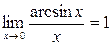 ,
, 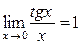 ,
, 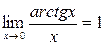 . (2.6)
. (2.6)
Приклад 2.20. Знайти границю 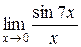 .
.
Розв’язання. При х 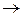 0, 7х також прямує до нуля, тому, помноживши чисельник і знаменник на 7, одержимо
0, 7х також прямує до нуля, тому, помноживши чисельник і знаменник на 7, одержимо
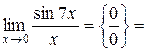
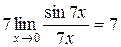 .
.
Зауваження.Вирази
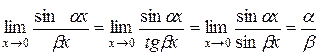
називаються робочими формулами першої визначної границі.
Приклад 2.21.Знайти границю: 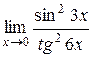 .
.
Розв’язання.Використовуємо робочу формулу першої визначної границі та знаходимо квадрат границі, отримуємо:
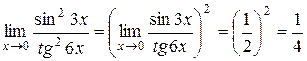 .
.
Приклад 2.22.Знайти границю 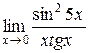 .
.
Розв’язання. При х 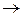 0, маємо невизначеність
0, маємо невизначеність 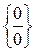 тому, замінюючи
тому, замінюючи 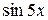 еквівалентним
еквівалентним 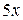 , отримуємо:
, отримуємо:
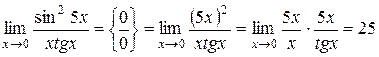 .
.
Приклад 2.23.Знайти границю 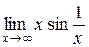 .
.
Розв’язання. 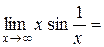
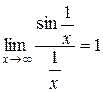 за формулою (2.5), тому що
за формулою (2.5), тому що 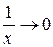 при
при 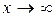 .
.
Друга визначна границя
Вираз
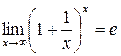 (2.7)
(2.7)
називається другою визначною границею. число e ірраціональне. Наближене значення e » 2,7182818. Співвідношення (2.7) можна записати у виді
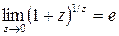 . (2.8)
. (2.8)
Другу визначну границюзастосовують при розкритті невизначеності 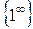 .
.
Приклад 2.24.Знайти границю 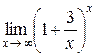 .
.
Розв’язання. При х 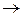
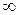 , маємо невизначеність
, маємо невизначеність 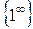 тому, перетворюючи вираз, що знаходиться під знаком границі, одержимо
тому, перетворюючи вираз, що знаходиться під знаком границі, одержимо
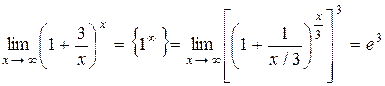 .
.
Зауваження.Вирази:
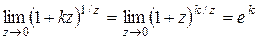 ,
,
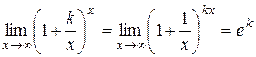 . (2.9)
. (2.9)
є робочими формулами другої визначної границі.
Приклад 2.25.Знайти границю 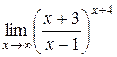 .
.
Розв’язання.При х 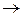
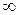 , маємо невизначеність
, маємо невизначеність 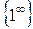 . використовуємо властивість
. використовуємо властивість 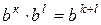 .
.
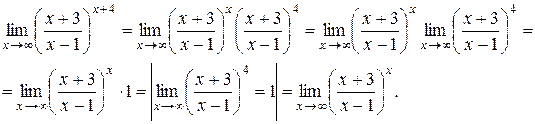
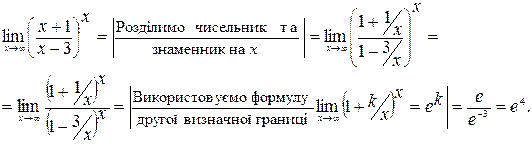
Приклад 2.26.Знайти границю 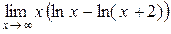 .
.
Розв’язання.Спочатку перетворимо вираз, що стоїть під знаком границі, використовуючи властивості логарифмів
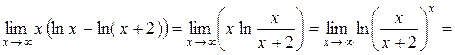
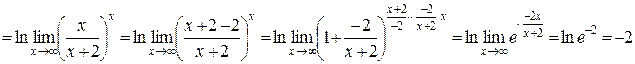
Приклад 2.27.Знайти границю 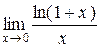 .
.
Розв’язання.При х 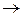 0, маємо невизначеність
0, маємо невизначеність 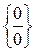 тому, виконавши перетворення з використанням властивостей логарифмів, одержимо
тому, виконавши перетворення з використанням властивостей логарифмів, одержимо
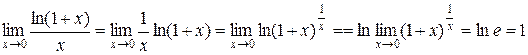 .
.
Приклад 2.28.Знайти границю 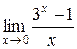 .
.
Розв’язання. При х 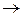 0, маємо невизначеність
0, маємо невизначеність 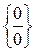 тому переходимо до нової змінної:
тому переходимо до нової змінної:
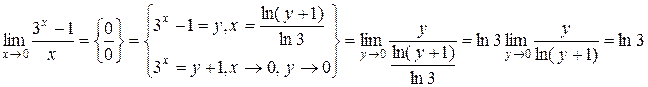
Неперервність функції
