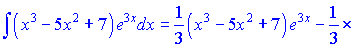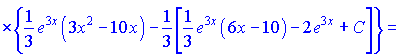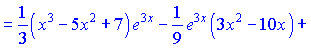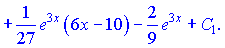Основні методи інтегрування
1. Безпосереднє інтегрування.
2. Метод заміни змінної
3. Інтегрування по частинах.
Безпосереднім інтегруванням будемо називати інтегрування за допомогою властивостей невизначеного інтеграла, тотожних перетворень підінтегральної функції і таблиці основних інтегралів.
Приклад 1.
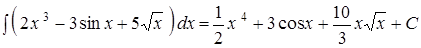 .
.
В основі методу підстановки (або методу заміни змінної) обчислення невизначених інтегралів лежить таке твердження, яке є наслідком правила диференціювання складеної функції:
Нехай дано функції 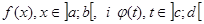 , і нехай існує складена функція
, і нехай існує складена функція 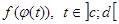 . Якщо функція
. Якщо функція 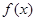 має первісну
має первісну 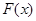 , а функція
, а функція 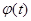 диференційована, то функція
диференційована, то функція 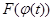 є первісною для функції
є первісною для функції 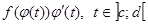 , і тому
, і тому
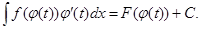
Приклад 1. Обчислити інтеграл 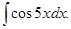
Розв’язання. Замінимо змінну 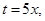 тоді
тоді 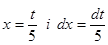 ,
,
отже,
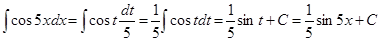 .
.
Приклад 2. Обчислити інтеграл
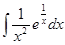 .
.
Розв’язання. Припустимо, що 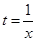 , тоді
, тоді 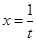 і
і 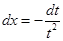 . Отже,
. Отже,
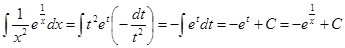 .
.
Інтегрування по частинах.
За правилом диференціювання добутку маємо
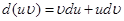 .
.
Тому
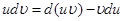
Якщо похідні (або, що те саме, диференціали) двох функцій рівні, то їх невизначені інтеграли збігаються. Тому
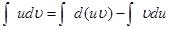
Використовуючи властивість невизначених інтегралів:
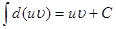 ,
,
дістанемо формулу
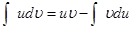 (1)
(1)
Цю формулу називають формулою інтегрування частинами.
Приклад 1. Обчислити інтеграл 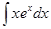
Розв’язання. Припустивши
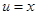 ,
, 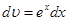 ,
,
тоді
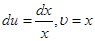
Звідси за формулою (1) матимемо
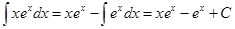
Приклад 2. Обчислити інтеграл 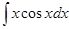 .
.
Розв’язання. Припустимо, що 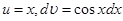
тоді 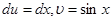
Тому, використовуючи формулу (1), маємо
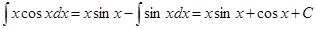
Використовуючи формулу інтегрування частинами для відшукання інтегралів від добутку, важко дати загальне правило для визначення того, який співмножник в підінтегральному виразі слід позначити через 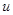 і який через
і який через 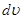 . Водночас при визначенні інтегралів необхідно, щоб
. Водночас при визначенні інтегралів необхідно, щоб 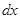 обов’язково входило у вираз для
обов’язково входило у вираз для 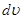 і цей вираз був легко інтегрованим, а також щоб інтеграл
і цей вираз був легко інтегрованим, а також щоб інтеграл 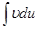 був простішим від вихідного. Так, наприклад, для інтегралів виду
був простішим від вихідного. Так, наприклад, для інтегралів виду 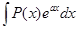 ,
, 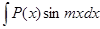 ,
, 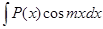 за
за 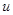 беруть многочлен
беруть многочлен 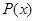 , а для інтегралів виду
, а для інтегралів виду 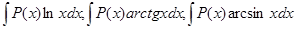 за
за 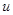 беруть відповідно
беруть відповідно 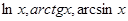
Якщо в інтегралах першого виду многочлен 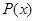 вищий від першого степеня, то формулу інтегрування частинами треба застосовувати кілька разів.
вищий від першого степеня, то формулу інтегрування частинами треба застосовувати кілька разів.
Приклад 3. Знайти інтеграл 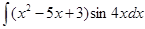
Розв’язання. Припустимо, що 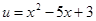 і
і 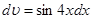 , тоді
, тоді 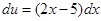 і
і 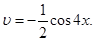 Тому
Тому
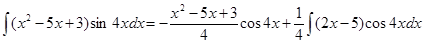

Останній інтеграл знайдемо інтегруванням частинами.
Припустимо тепер, що 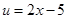 і
і 
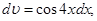 тоді
тоді 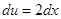 і
і 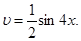 Отже,
Отже,
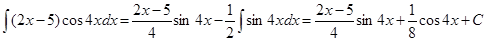
Таким чином,
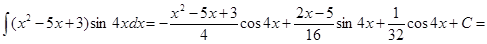
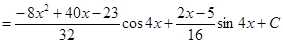
Формула інтегрування частинами застосована і для знаходження інтегралів виду
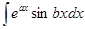 і
і 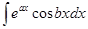 . Для знаходження таких інтегралів формулу інтегрування частинами застосовують послідовно двічі, причому обидва рази за
. Для знаходження таких інтегралів формулу інтегрування частинами застосовують послідовно двічі, причому обидва рази за 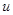 беруть або показникові функцію, або тригонометричну. Після дворазового інтегрування частинами дістають лінійне рівняння відносно шуканого інтеграла.
беруть або показникові функцію, або тригонометричну. Після дворазового інтегрування частинами дістають лінійне рівняння відносно шуканого інтеграла.
Приклад 4. Обчислити інтеграл 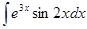
Розв’язання. Припустимо, що 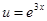 і
і  , звідки
, звідки 
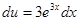 і
і 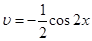 . Тому
. Тому
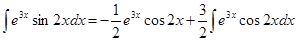 (2)
(2)
Для знаходження останнього інтеграла використаємо ще раз формулу інтегрування частинами:
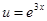 і
і 
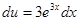 і
і 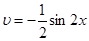
Тоді 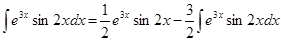
Підставивши цей вираз у рівність (2) дістанемо
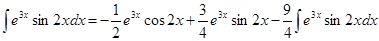
Отже,
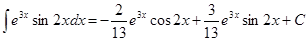
5.Визначений інтеграл: поняття,геометричний і економічний зміст,властивості.
Поняття визначеного інтегралу
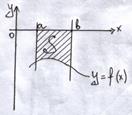
Розглянемо плоску фігуру, обмежену графіком неперервної та невід’ємної на відрізку [a; b] функції f(x), відрізком [a; b], та і прямими x=a та x=b.
Отримана фігура називається криволінійною трапецією. Обчислимо її площу. Для цього розіб’ємо відрізок [a; b] на n рівних відрізків. Довжини кожного з відрізків дорівнюють Δx.
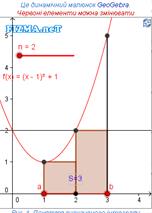
Рис. 1. Поняття визначеного інтегралу
На кожному відрізку, побудуємо прямокутники з висотами f(xk-1) (Рис. 1).
Площа кожного такого прямокутника дорівнює Sk = f(xk-1)Δxk.
Площа всіх таких прямокутників дорівнює 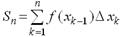 .
.
Цю суму називають інтегральною сумою для функції f(x).
Якщо n→∞ то площа побудованої таким чином фігури буде все менш відрізнятись від площі криволінійної трапеції.
Означення. Границя інтегральної суми коли n→∞ називається визначеним інтегралом, і записується це так :. 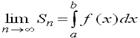 читається: "інтеграл від a до b f від xdx"
читається: "інтеграл від a до b f від xdx"
Число а називається нижньою межею інтегрування, b – верхньою межею інтегрування, відрізок [a; b] – проміжок інтегрування.
Властивості визначеного інтегралу
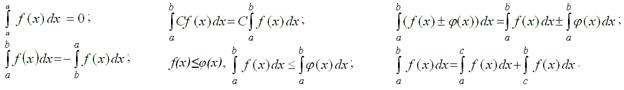
Використання поняття визначеного інтегралу в економіці
Визначення загального обсягу випущеної продукції
Нехай деяка фірма випускає один вид продукції, використовуючи один ресурс. Виробнича функція фірми має вигляд q=q(x), де x - затрати ресурсу, а q - обсяг випуску. Затрати ресурсу x є функцією від часу t, наприклад, x=x(t).
Тоді загальний обсяг продукції Q за час від T0 до T1 обчислюється за допомогою визначеного інтегралу 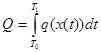
.
При , x(t)=100e0,2t, T0=0 та T1=5 (років) загальний обсяг випущеної за п’ять років продукції
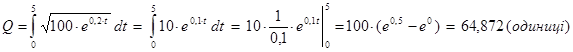
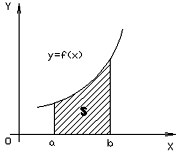
Геометричний зміст визначеного інтеграла: 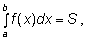 де S- площа фігури, обмеженої графіком функції y = f(x) і прямими х = а, х = b і y = 0.
де S- площа фігури, обмеженої графіком функції y = f(x) і прямими х = а, х = b і y = 0.
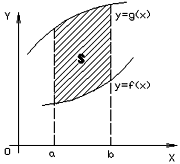
Площа фігури, обмеженої графіками функцій f(x), g(x) і прямими х = а і х = b дорівнює:
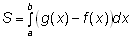
Приклад 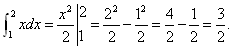
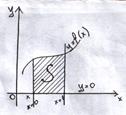
Геометричний зміст визначеного інтегралу: якщо | 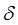 к|→0, то площа ступінчастої фігури наближається до площі криволінійної трапеції, обмеженої прямими х=а, х=b, у=0 і кривою у=f(x).
к|→0, то площа ступінчастої фігури наближається до площі криволінійної трапеції, обмеженої прямими х=а, х=b, у=0 і кривою у=f(x).
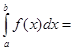 S (при f(x)≥0, x є [a;b]). Якщо f(x)≤0, то
S (при f(x)≥0, x є [a;b]). Якщо f(x)≤0, то 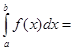 -S.
-S.
6.Формула Ньютона-Лейбніца
Нехай функція f неперервна на відрізку [а, b] та F — певна первісна для f на цьому відрізку, тоді:
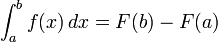
Ця формула називається формулою Ньютона—Лейбніца. Іноді її називають основною формулою інтегрального числення. Для скорочення запису часто застосовуеться позначення:
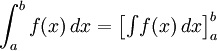
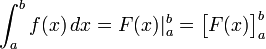
7.Застосування.Площа плоскої фігури.Криволінійна трапеція.
План 1.1. Обчислення площі в декартових координатах Коли розглядається площа криволінійної трапеції, обмеженої віссю  кривою кривою 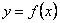 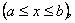 причому причому 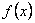 на відрізку на відрізку  може бути як додатною, так і від’ємною, то площа такої криволінійної трапеції обчислюється за формулою може бути як додатною, так і від’ємною, то площа такої криволінійної трапеції обчислюється за формулою 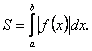 (10.1) Нехай у прямокутній системі координат фігура (10.1) Нехай у прямокутній системі координат фігура  (рис.10.1) обмежена кривими (рис.10.1) обмежена кривими 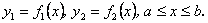 Виділимо у фігурі смужку шириною Виділимо у фігурі смужку шириною  . Її довжина дорівнюватиме . Її довжина дорівнюватиме  . Тоді площа смужки . Тоді площа смужки 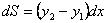 . Звідси . Звідси 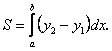 Отже, Отже, 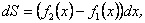 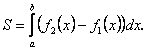 (10.2) (10.2) 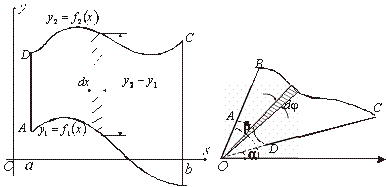 Рис.10.1 Рис.10.2 Обчислимо тепер площу криволінійної трапеції у випадку, коли крива задана рівняннями в параметричній формі Рис.10.1 Рис.10.2 Обчислимо тепер площу криволінійної трапеції у випадку, коли крива задана рівняннями в параметричній формі 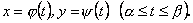 (10.3) Нехай рівняння (10.3) визначають деяку функцію (10.3) Нехай рівняння (10.3) визначають деяку функцію 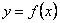 на відрізку на відрізку  а тому площа криволінійної трапеції може бути обчислена за формулою а тому площа криволінійної трапеції може бути обчислена за формулою 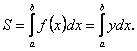 Зробивши заміну в цьому інтегралі Зробивши заміну в цьому інтегралі 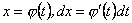 і враховуючи, що і враховуючи, що 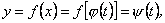 одержимо одержимо 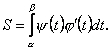 (10.4) 1.2. Площа криволінійного сектора в полярних координатах Нехай криві, що обмежують фігуру, задані рівнянням в полярній системі координат і відрізками двох полярних радіусів (рис. 10.2) .Знайдемо площу фігури (10.4) 1.2. Площа криволінійного сектора в полярних координатах Нехай криві, що обмежують фігуру, задані рівнянням в полярній системі координат і відрізками двох полярних радіусів (рис. 10.2) .Знайдемо площу фігури  якщо: якщо: 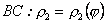 , , 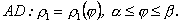 У фігурі У фігурі  виділимо сектор з центральним кутом виділимо сектор з центральним кутом  Вважатимемо, що дуги, які обмежують сектор Вважатимемо, що дуги, які обмежують сектор  , є дугами кіл радіусів , є дугами кіл радіусів  . Очевидно, що площа сектора . Очевидно, що площа сектора  між дугами між дугами  i i  дорівнює дорівнює 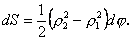 Інтегруючи, одержимо Інтегруючи, одержимо 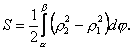 (10.5) Приклад 1. Знайти площу фігури, обмеженої гіперболою (10.5) Приклад 1. Знайти площу фігури, обмеженої гіперболою 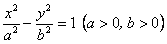 , віссю , віссю  і прямою, яка з’єднує точку і прямою, яка з’єднує точку 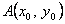 , що лежить на гіперболі, з початком координат. Р о з в ’ я з о к. З рівняння гіперболи маємо , що лежить на гіперболі, з початком координат. Р о з в ’ я з о к. З рівняння гіперболи маємо  Щоб знайти площу заштрихованої на рис.10.3 фігури, досить знайти площу фігури Щоб знайти площу заштрихованої на рис.10.3 фігури, досить знайти площу фігури  , а потім від площі трикутника , а потім від площі трикутника  відняти площу фігури відняти площу фігури  . Отже, . Отже, 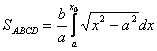 . Найкращим методом для обчислення цього інтеграла є інтегрування частинами. В результаті інтегрування дістанемо Оскільки то . Найкращим методом для обчислення цього інтеграла є інтегрування частинами. В результаті інтегрування дістанемо Оскільки то  . Цікаво, що цю площу можна записати у вигляді . Цікаво, що цю площу можна записати у вигляді  Рис.10.3 Рис.10.4 Рис.10.3 Рис.10.4  , де , де  - функція, обернена відносно функції - функція, обернена відносно функції  . Пропонується переконатися в цьому самостійно. Приклад 2. Знайти площу фігури, обмеженої кривою . Пропонується переконатися в цьому самостійно. Приклад 2. Знайти площу фігури, обмеженої кривою  . Р о з в ’ я з о к.Перейшовши в цьому рівнянні до прямокутної системи координат, легко встановити, що відповідна крива є центрально-симетричною відносно системи координат. Крім того, із заданого рівняння видно, що . Р о з в ’ я з о к.Перейшовши в цьому рівнянні до прямокутної системи координат, легко встановити, що відповідна крива є центрально-симетричною відносно системи координат. Крім того, із заданого рівняння видно, що  , тобто крива повністю знаходиться всередині кола радіуса , тобто крива повністю знаходиться всередині кола радіуса  з центром в початку координат, що дотикається вона до кола лише в точках з центром в початку координат, що дотикається вона до кола лише в точках  , проходить через початок координат при , проходить через початок координат при  , дотикаючись до прямих , дотикаючись до прямих  . Отже графік заданої функції має вигляд чотирипелюсткової троянди (рис. 10.4). Очевидно, що для обчислення площі досить знайти площу заштрихованої фігури і потім її помножити на 8. Отже, . Отже графік заданої функції має вигляд чотирипелюсткової троянди (рис. 10.4). Очевидно, що для обчислення площі досить знайти площу заштрихованої фігури і потім її помножити на 8. Отже, 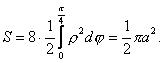 |
8.Метод заміни змінної (метод підстановки)
Полягає в тому, що деякий вираз позначають новою змінною, а потім весь підінтегральний вираз виражають через цю нову змінну.
Приклад: 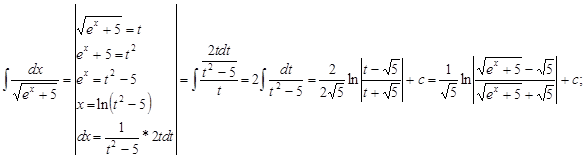
В загальному випадку
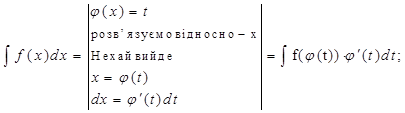
Якщо останній інтеграл виявиться простішим від початкового, то заміна вдала.
Для цього методу бажано знати, які заміни змінних в тих чи інших випадках приведуть до спрощення інтегралу.
9.Метод інтегрування частинами.
Із формули диференціала добутку 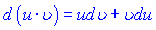 інтегруванням двох частин рівності одержумо формулу інтегрування частинами
інтегруванням двох частин рівності одержумо формулу інтегрування частинами 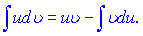
За цією формулою знаходження інтеграла  зводиться до знаходження іншого інтеграла
зводиться до знаходження іншого інтеграла  Застосовувати цю формулу потрібно в тих випадках, коли
Застосовувати цю формулу потрібно в тих випадках, коли  легко знаходитися. Якщо неправильно вибрати , то завдання навпаки може уладнитись. Для застосування формули інтегрування частинами до інтегралу
легко знаходитися. Якщо неправильно вибрати , то завдання навпаки може уладнитись. Для застосування формули інтегрування частинами до інтегралу 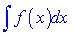 необхідно підінтегральний вираз
необхідно підінтегральний вираз 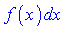 представити в вигляді добутку двох множників
представити в вигляді добутку двох множників  та
та 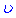 . За
. За 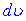 завжди вибирають такий вираз, що містить
завжди вибирають такий вираз, що містить  . Його інтегруванням можна знайти . За в більшості випадків приймається функція, яка при диференціюванні спрощується.
. Його інтегруванням можна знайти . За в більшості випадків приймається функція, яка при диференціюванні спрощується.
В такий спосіб на першій погляд важкі і незрозумілі, з точи зору обчислень, інтеграли можна швидко звести до табличного вигляду.
Розглянемо приклади інтегрування частинами.
Приклад 1.
Обчислити інтеграли
a) 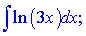
b) 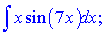
c) 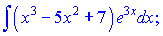
Розв'язок.
а) Даний інтеграл один з класичних в курсі вищої математики. Функції 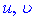 підбираємо таким чином
підбираємо таким чином 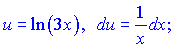
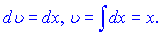
Згідно формул інтегрування частинами маємо 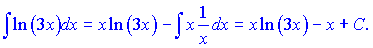
б) Для даного інтеграла 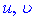 вибираємо у вигляді
вибираємо у вигляді

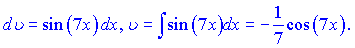
За формулою отримаємо
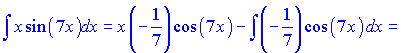
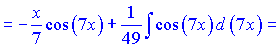
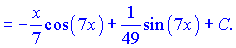
в) В даному випадку вибараємо наступними
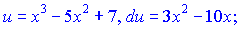
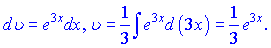
Підставляємо в інтеграл
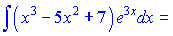
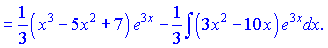
Бачимо, що знову отримали інтеграл до якого потрібно застосувати правило інтегрування частинами
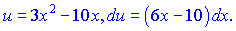
Формли для 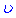 беремо з попереднього інтегрування. Підставляючи в інтеграл, отримаємо
беремо з попереднього інтегрування. Підставляючи в інтеграл, отримаємо
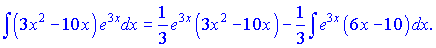
До останнього інтегралу знову застосовуємо правило
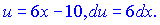
Друга змінна залишається без змін. Залишився один крок до повного обчислення.
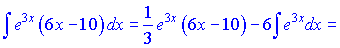
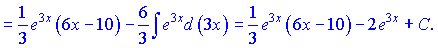
Підставляючи в вихідну формулу, матимемо