Линейный закон фильтрации Дарси

В. А. Евдокимова

И. Н. Кочина

Сборник задач

По подземной

Гидравлике

Учебное пособие для вузов

Издание второе, стереотипное

Перепечатка с издания 1979 г.

Первое издание допущено Министерством высшего

и среднего специального образования СССР в

качестве учебного пособия для студентов высших

учебных заведений, обучающихся по специальности

«Технология и комплексная механизация разработки нефтяных и газовых месторождений»

АльянС

Москва 2007

УДК 622.276 (0.75.8)

ББК

Е15

Евдокимова В.А., Кочина И.Н.

Е15 Сборник задач по подземной гидравлике:

Учебное пособие для вузов. — 2-е изд., стереотипное. Перепечатка с издания 1979 г. - М.: ООО ИД «Альянс», 2007. - 168 с.

Приведенные в учебном пособии ладами, можно использовать при проектировании разработки нефтяных и газовых месторождений. Первое, издание выпущено в 1979 году издательством «Недра». Учебное пособие рассчитано на студентов нефтяных вузов и факультетов.

ISBN 978-5-903034-13-0

© ООО ИД «Альянс», 2007

ЕВДОКИМОВА Вера Алексеевна

КОЧИНА Ираида Николаевна

Сборник задач по подземной гидравлике

Учебное пособие для вузов

Издание второе, стереотипное

Перепечатка с издания 1979 г.

Подписано в печать 27.10.06. Формат 60x90/16.

Гарнитура Литературная. Печати офсетная Исч. л. 10,5.

Тираж 1000 экз. Заказ 61061

ООО Издательский дом «Альянс»

105120, Москва, ул. Сергия Радонежского, д.9, стр. 5

Тел./факс (499) 973-06-80, 973-09-41

973-17-82, 973-17-96, 973-18-56

[email protected]

Отпечатано с готовых диапозитивов

Г. Саратов, ул. Волжская, д.28

ЗАО "Типография "Полиграфист"

ПРЕДИСЛОВИЕ

В сборник включены задачи, которые можно использовать при проектировании нефтяных и газовых месторождений, ре­шении различных проблем гидротехники, инженерной геологии, гидрогеологии, ирригации и горного дела. Решение многих задач подземной гидравлики полезно также при расчете ис­кусственных фильтров различных конструкций, пористых катализаторов и т. д.

При составлении сборника задач авторы использовали мно­голетний опыт преподавания курса «Подземная гидравлика» в Московском институте нефтехимической и газовой промышлен­ности им. акад. И. М. Губкина. В сборник, в основном, вошли задачи, которые предлагались студентам на практических за­нятиях.

Настоящее пособие предназначено также для студентов специальностей «Геология и разведка нефтяных и газовых ме­сторождений» и «Экономика и организация нефтяной и газо­вой промышленности».

Сборник задач состоит из 15 глав. К каждой главе дает­ся краткая теория. Ко всем задачам имеются ответы. Типовые и наиболее сложные задачи приведены с решениями. В реше­ниях некоторых задач даются выводы формул, отсутствующие в учебной литературе.

В сборник входят задачи на определение фильтрационных характеристик пластов, расчет производительности нефтяных игазовых эксплуатационных и нагнетательных скважин в од­нородных и неоднородных по проницаемости пористых плас­тах, а также в деформируемых трещиноватых пластах, учет интерференции скважин (совершенных и несовершенных), рас­чет продвижения водонефтяного контакта, определение высо­ты подъема конуса подошвенной воды при эксплуатации неф­тяных или газовых месторождений с подошвенной водой, оп­ределение дебитов и распределения давления при движении га­зированной жидкости в пористой среде, изменение дебитов и давлений при нестационарном движении упругой жидкости и газа в деформируемой пористой среде, вытеснение нефти водой по теории Баклея — Леверетта и др.

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ФИЛЬТРАЦИИ

Фильтрация

Фильтрацией называется движение жидкостей, газов и их смесей в пористых и трещиноватых средах, т. е. в твер­дых телах, пронизанных системой сообщающихся между собой пор и микротрещин.

Фильтрация жидкостей и газов по сравнению с движением в трубах и каналах обладает некоторыми специфическими осо­бенностями.

Фильтрация происходит по чрезвычайно малым в попереч­ных размерах норовым каналам при очень малых скоростях движения жидкостей. Силы трения при движении жидкости в пористой среде очень велики, так как площади соприкоснове­ния жидкостилощади соприкоснове­ния жидкое с твердыми частицами огромны.

Пористая среда характеризуется коэффициентами пористо­сти и проснетпости.

Коэффициент пористости тесть отношение объема­ пор (τ_пор) ко всему объему пористой среды (τ)

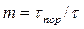(I.1)

Под пористостью в теории фильтрации понимается активная пористость, которая учитывает только те поры и микротрещины, которые соединены между собой и че­рез которые может фильтроваться жидкость.

Коэффициентом просветности п называется от­ношение площади просветов (ω_просв) в данном сечении пори­стой среды ко всей площади этого сечения (ω)

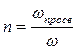(I.2)

Можно показать, что среднее по длине пласта значение просветности равно пористости, т. е.

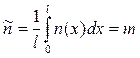(I.3)

поэтому среднее значение площади просветов

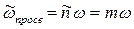
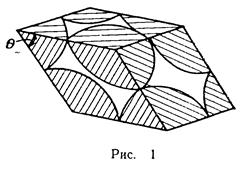
Упрощенной моделью пористой среды является модель фиктивного грунта. Фиктивный грунт состоит из шари­ков одного диаметра, уложенных определенным образом. Основным элементом (основной ячейкой) фиктивного грунта яв­ляется ромбоэдр, который получится, если принять центры восьми соприкасающихся частиц за вершины углов (рис. 1), В зависимости от острого угла θ боковой грани ромбоэдра ук­ладка шаров более или менее плотная.

Угол θ изменяется в пределах от 60° до 90°. Углу θ = 60° соответствует наиболее плотная укладка шаров, углу θ = 90° — наиболее свободная.

Пористость фиктивного грунта определяется по формуле Ч. Слихтера

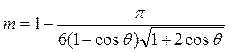(I.4)

из которой следует, что пористость зависит не от диаметра частиц, а лишь от их взаимного расположения, которое опре­деляется углом θ.

Чтобы формулы для фиктивного грунта можно было при­менять для естественного грунта, нужно заменить реальный грунт эквивалентным ему фик­тивным, который должен иметь такое же гидравличес­кое сопротивление, как у ес­тественного грунта.

Диаметр частиц такого фиктивного грунта называется эффек­тивным диаметром (d₃). Эффективный диаметр оп­ределяется в результате ме­ханического анализа грунта. Его просеивают через набросит с различной площадью отверстий и, таким образом, разде­ляют на фракции. За средний диаметр каждой фракции прини­мают среднее арифметическое крайних диаметров, т.е.

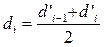
Затем строят кривую механического (фракционного) соста­ва грунта, откладывая по оси абсцисс средние диаметры фрак­ций d_i а но оси ординат — сумму масс фракций Δg₁+ Δg₂ + + ... + Δg_i в % от общей массы.

Последняя точка кривой имеет абсциссу, равную d_n, и ор­динату Δg₁+ Δg₂+... + Δg_n =100% (рис. 2).

Существует много способов определения эффективного диаметра. По способу А. Газена d_э определяется по кривой механического состава. За эффективный принимается такой диаметр шарообразной частицы, который соответствует сумме масс всех фракций, начиная от нуля и кончая этим диамет­ром, равной 10%. Надо найти, кроме того, диаметр d_0, который соответствует сумме масс фракций,, равной 60%. Коэф­фициент однородности d_o/d_э должен быть не более 5 (d_o/d_э ≤ 5) и d_э должен лежать в пределах от 0,1 до 3 мм.

По способу Крюгера — Цункера используют данные механического анализа грунта и определяют d_э по формуле

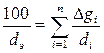(I.5)

Скоростью фильтрации w называется отношение объемного расхода жидкости к площади поперечного сечения пласта, нормального к направле­нию движения жидкости

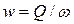(I.6)

Скорость фильтрации представ­ляет собой фиктивную скорость, с которой двигалась бы жидкость, если бы пористая среда отсутство­вала (m=1).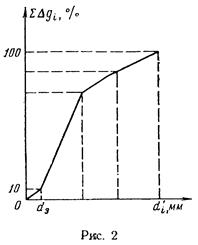

Средняя скорость движения жидкости v равна отношению объ­емного расхода к площади просве­тов ω_просв (живому сечению пото­ка)

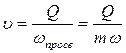(I.7)

Скорость фильтрации и средняя скорость движения связа­ны соотношением

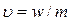
Линейный закон фильтрации Дарси.