Отже функція ні парна, ні непарна, неперіодична

Дослідження функції, побудова графіка

Дослідження функцій займає немало часу при розв'язуванні контрольних, домашніх завдань і щоб навчитися швидко розв'язувати потрібна інструкція, яка пояснює порядок дій і для чого це потрібно. Така інструкція розроблена викладачами і узагальнена на всі типи функцій вже давно, а ми її називаємо – загальна схема дослідження функції.

Щоб дослідити функцію 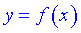та побудувати її графік необхідно:

1) знайти область визначення функції, тобто множину всіх точок для яких існує значення функції;

2) знайти (якщо вони існують) точки перетину графіка з координатними осями. Для цього потрібно у рівняння 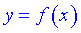підставити , а також розв'язати рівняння 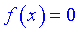для відшукання точок перетину з віссю ;

3) дослідити функцію на періодичність, парність і непарність. У деяких випадках це можна зробити візуально за самим виглядом функції, якщо ні- то проводимо перевірку:

1. 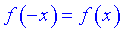– функція парна;

2. 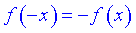– функція непарна;

Функція періодична, – період функції.

Таким чином, якщо маємо парну функцію , то достатньо побудувати її для додатніх значень , після чого відобразити симетрично відносно осі абсцис на решту області. У випадку непарної функції графік буде симетричний відносно початку координат. Для прикладу, якщо маємо непарну функцію, графік якої належить першій чверті другу половину отримаємо поворотом першої чверті на 180 градусів (третя чверть).

Періодичними є переважно фукнкції, складені з простих тригонометричних та деякі параметрично задані функції.

4) знайти точки розриву та дослідити їх (такими точками є краї інтервалів визначення функції);

5) знайти інтервали монотонності, точки екстремумів та значення функції в цих точках;

6) знайти інтервали опуклості, вгнутості та точки перегину;

7) знайти асимптоти кривої;

Побудувати графік функції.

Більшість з цих пунктів розлядалася на практиці в попередніх статтях, тому детально розписувати ми їх не будемо. Також не переживайте, якщо знайдете план в літературі чи інтернеті, який містить більше або менше пунктів. Пам'ятайте, що мета їх всіх – допомогти при побудові графіка функції. Перейдемо до практичної частини і досслідимо за схемою функцію.

Приклад 1.

Дослідити функцію і побудувати її графік (Дубовик В.П., Юрик І.І. "Вища математика. Збірник задач" )

І (5.889)

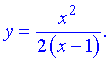
Розв'язання:

1) Функція визначена всюди, крім точки в якій знаменник перентворюється в нуль 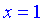. Область визначення складається з двох інтервалів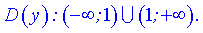

При підстановці матимемо

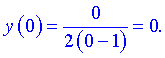
Таку ж саму точку отримаємо, якщо прирівняємо функцію до нуля. Точка - єдина точка перетину з осями координат.

Перевірка на парність

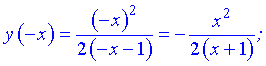
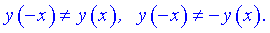
Отже функція ні парна, ні непарна, неперіодична.