Закон сохранения момента импульса для системы тел

Рассмотрим замкнутую систему тел, то есть систему, на которую или не действуют внешние силы, или силы и моменты сил скомпенсированы. Для некоторого тела основной закон динамики вращательного движения имеет вид 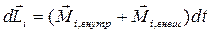. Представим, что это уравнение написано столько раз, сколько тел в системе. Просуммируем эти уравнения. Сумма моментов внутренних сил будет равна нулю, так как внутренние силы между телами действуют попарно и противоположны. Сумма моментов внешних сил будет равна нулю по условию замкнутости системы тел. В результате изменение суммы моментов импульсов тел будет равно нулю 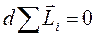. Отсюда следует закон сохранения момента импульса: в замкнутой системе тел сумма моментов импульсов тел постоянна

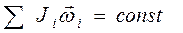. (12.4)

Или, сумма моментов импульсов замкнутой системы тел до начала процесса равна сумме моментов импульсов тел после окончания процесса.

Например, при включении электродвигателя якорь начинает вращаться в одну сторону, а корпус электродвигателя – в другую, и если корпус не закреплен, то электродвигатель может опрокинуться. Для изменения положения космической станции вместо ракетных двигателей применяют более эффективные гиродины – это небольшие электродвигатели. При вращении якоря гиродина в одном направлении станция поворачивается в противоположном направлении и останавливается в момент выключения гиродинов. Система из трех гиродинов со взаимно перпендикулярными осями позволяет ориентировать станцию в любое положение. Это гораздо удобнее, чем применение для ориентации ракетных двигателей.

Аналогично, космонавт в соответствии с законом сохранения импульса не может никакими действиями изменить положение центра масс в пространстве, но может повернуться относительно любой оси, проходящей через центр масс. Для этого достаточно начать вращение руками или ногами и повернуться в противоположном направлении.

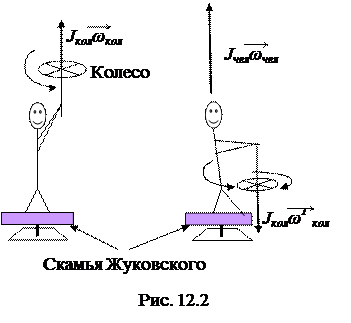
Рассмотрим пример вращения человека на скамье Жуковского. Пусть, когда он неподвижен, ему подали вращающееся относительно вертикальной оси колесо (рис.12.2). Затем стержень колеса повернули на угол 180^о. Момент импульса колеса повернется на 180^о, но не изменится по величине. Относительно вертикальной оси моменты сил, если пренебречь трением в подшипниках, отсутствуют. Поэтому проекция суммы моментов импульса на ось сохраняется: 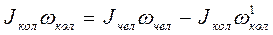. Суммарный момент импульса не изменится, но скамья вместе с человеком будет вращаться в том же направлении, что и колесо до поворота с моментом импульса 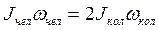. Вращение человека происходит за счет работы момента сил человека.

Закон сохранения момента импульса, наряду с законом сохранения импульса и закона сохранения энергии, является фундаментальным законом природы. Он позволяет определить параметры движения тел после процесса взаимодействия тел, даже не зная законов взаимодействия тел.

Гироскоп

Гироскопы – это тела, имеющие форму тел вращения, быстро вращающиеся относительно оси симметрии и способные изменять направление оси в пространстве. Момент импульса гироскопа должен быть большим по сравнению с импульсом момента силы L >> M ∆t, который действует на гироскоп за время наблюдения Δt. Свойствами гироскопа обладают небесные тела, роторы турбин и электродвигателей, колеса и маховики, электроны атомов. Гироскоп – основной элемент гироскопических приборов – гирокомпаса, автопилотов самолетов и ракет. Если гироскоп уравновешен, на него не действует момент сил тяжести, то, согласно закону сохранения момента импульса, в инерциальной системе отсчета (относительно звезд) положение оси будет постоянно, хотя Земля будет поворачиваться. Это свойство используется в гирокомпасах. Свойство сохранять положение оси в пространстве используется для стабилизации экипажей монорельсового транспорта. Применяется для стабилизации корпусов кораблей при качке, башен танков, поездов на магнитном подвесе и на воздушной подушке.

Чтобы ось гироскопа могла поворачиваться в пространстве, его помещают в так называемый карданов подвес. Карданов подвес представляет собой три рамки, оси вращения которых взаимно перпендикулярны и пересекаются в точке, называемой центром подвеса О. Таким образом трехстепенной гироскоп может свободно вращаться относительно трех осей (рис. 12.2).

Если к быстровращающемуся гироскопу приложить момент пары сил F₁ – F₂ (рис. 12.2), то гироскоп ведет себя неожиданно: его ось поворачивается не вокруг оси Оx, а вокруг оси Оz. Это явление поворота оси гироскопа с угловой скоростью, перпендикулярной направлению вектора момента силы, называется прецессией. Для вывода формулы угловой скорости прецессии применим к гироскопу основной закон динамики вращательного движения: изменение момента импульса тела dL равно импульсу момента силы М dt

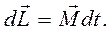(12.5)

Пусть на быстровращающийся гироскоп действует момент силы М, перпендикулярный моменту импульса L (рис. 12.3). Сложим приращение вектора момента импульса dL, вызванное действием момента силы, с исходным моментом импульса: 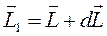. Как видно из рисунка, вектор момента импульса повернется в новое положение L₁ вместе с осью гироскопа вокруг оси Оz.

Но благодаря карданову подвесу с ними вместе повернется и вектор момента силы и займет новое положение M₁, опять оказавшись перпендикулярным новому моменту импульса L₁. Через последующее время dt момент импульса получит новое приращение dL₁, параллельное моменту силы M₁, и момент импульса получит новое положение 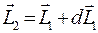ит.д. Ось гироскопа будет поворачиваться вокруг оси Oz так, как будто вектор момента импульса пытается «догнать» убегающий вектор момента силы. Таким образом, прецессия – это явление поворота оси вращения гироскопа под действием перпендикулярного к оси момента силы, при котором вектор момента импульса поворачивается по кратчайшему направлению к вектору момента силы.

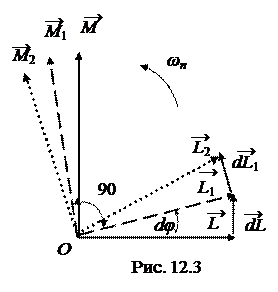Определим в элементарной теории гироскопа угловую скорость прецессии. Угловая скорость по определению равна отношению угла поворота ко времени 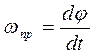. Угол поворота оси 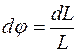. Подставив приращение момента импульса 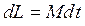, согласно основному уравнению динамики вращательного движения, получим

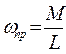^. (12.6)

Если ось гироскопа принудительно поворачивать, то на гироскоп должен действовать со стороны подшипников оси момент сил. Вектор момента сил должен быть направлен вдоль вектора dL. А на подшипники, согласно третьему закону Ньютона, будет действовать момент так называемых гироскопических сил противоположного направления. Момент гироскопических сил, согласно формуле (12.6) равен М = L ω_пов. Гироскопические силы воздействуют на подшипники быстро вращающихся роторов турбин, якорей электродвигателей транспортных средств при движении на повороте.

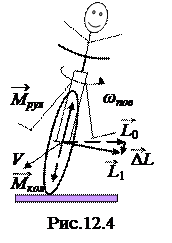Например, гироскопические силы позволяют ездить, не держась за руль, на велосипеде (рис.12.4). При наклоне велосипеда момент импульса переднего колеса L₀ получает приращение ΔL под действием момента силы на подшипники со стороны вилки 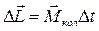. А на вилку руля, согласно третьему закону Ньютона, действует момент сил противоположного направления М_руль. Этот момент сил по правилу буравчика поворачивает руль с колесом на виде сверху против часовой стрелки, то есть вовнутрь поворота.

Задачи

1. Локомотив массой 200 т со скоростью 20 м/с движется на повороте радиусом 600 м. Затем, пройдя переходной участок в течении 20 с, движется прямолинейно. Определить момент сил и силы, действующие на рельсы на переходном участке. Длина локомотива 24 м.

2. Незакрепленный электродвигатель начал вращение и за 20 секунд набрал скорость 50 1/с. Определить момент сил, действующий на корпус двигателя. Момент инерции якоря 10 кг·м². Проверить, опрокинется ли двигатель, если масса двигателя 200 кг, высота оси 30 см, расстояние между опорами 40 см.

3. Якорь гиродина вращается с угловой скоростью 600 1/с. Якорь считать диском массой 0,5 кг и радиусом 5 см. Определить угловую скорость вращения космической станции, если момент инерции относительно оси, параллельной оси якоря, 80·10³ кг·м².

4. Локомотив движется на повороте радиусом 400 м со скоростью 10 м/с. Определить момент гироскопических сил, действующий подшипники якоря электродвигателя с моментом инерции 120 кг·м². Диаметр колес 1,18м, передаточное отношение зубчатой передачи 4,2. Определить гироскопические силы, действующие на подшипники якоря, если расстояние между ними 0,6 м.

5. Поезд движется на повороте радиусом 600 м со скоростью 20 м/с. Определить момент гироскопических сил, действующий на колесную пару. Колеса считать дисками, масса колеса 800 кг, колеса 1,02 м. Определить гироскопические силы, действующие не рельсы. Ширина колеи 1,52 м.

6. Турбина газотурбовоза вращается с угловой скоростью 400 об/с, момент инерции 8·10³ кг·м², ось вращения перпендикулярна бортам. Определить гироскопические силы, действующие на рельсы, если на стрелке направление движения изменилось на 5^о за 10 с. Ширина колеи 1,52 м.

7. Определить момент импульса Земли. Метеорит массой 1000 кг со скоростью 8 км/с по касательной к экватору и к орбите упал на Землю. Определить изменение скорости орбитального движения и изменение угловой скорости вращения Земли.

13. РЕЛЯТИВИСТСКАЯ МЕХАНИКА

Релятивистская механика это научная теория о движении тел со скоростями, близкими к скорости света. Это часть Специальной теории относительности (СТО), основателем которой является А. Эйнштейн (1905 г.). Необходимость возникновения СТО была обусловлена неоднозначными опытами по изучению распространения света в различных системах отсчета, неудачами в поисках светоносного эфира, в котором должен был бы распространяться свет, и неинвариантностью уравнений электродинамики Максвелла относительно преобразований Галилея. Проблемы были разрешены на основании двух постулатов Эйнштейна.

Специальная теория относительности изменила представления о пространстве и времени, которые в механике Ньютона считались не связанными друг с другом. Это первая, но не последняя, абстрактная научная теория, не соответствующая жизненному опыту, но подтвержденная экспериментально.

Постулаты СТО

1. Принцип относительности. Любые физические явления протекают одинаковым образом во всех инерциальных системах отсчета и описываются одинаковыми уравнениями. То есть законы природы инвариантны (имеют одинаковый вид). Для равноправия инерциальных систем отсчета вид уравнений не должен зависеть от скорости движения системы отсчета. Следовательно, никакими физическими опытами невозможно обнаружить движение системы отсчета, находясь внутри неё.

Итак, все инерциальные системы отсчета равноправны. Отсутствует в природе избранная абсолютная система отсчета – светоносный эфир, заполняющий мировое пространство, в котором движутся тела, свет.

2. Принцип инвариантности скорости света. Скорость света в вакууме одинакова во всех инерциальных системах отсчета.

То есть скорость света не зависит от скорости движения источника света, от скорости приемника света. Конечно, следует ожидать, что если в природе существует предельная скорость, то она одинакова во всех равноправных системах отсчета. Скорость света – это предельная скорость движения тел, предельная скорость распространения сигналов. Прямых экспериментальных доказательств постулата постоянства скорости света нет. Справедливость подтверждается экспериментальной проверкой следствий СТО, основанной на постулате постоянства скорости света.

Например, в середине поезда произошла вспышка света. Для пассажира свет одновременно достигнет головы и хвоста поезда. Для наблюдателя на перроне свет распространяется с такой же скоростью. Значит, свет раньше достигнет хвоста, который приближается световому импульсу, и позже придет к удаляющейся голове поезда. Отсюда следует, что в разных системах отсчета время течет неодинаково.

Преобразования Лоренца

Рассмотрим две инерциальные системы отсчета К и К', движущиеся относительно друг друга со скоростью V (рис. 13.1). Положение тела в этих системах отсчета в классической механике определяется преобразованиями Галилея

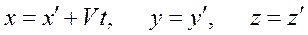. (13.1)

Время абсолютно и одинаково 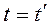. Преобразования Галилея неоднозначно объясняли эксперименты с распространением света, поэтому их следует заменить. Для объяснения опытов со светом Лоренц, ещё до создания СТО, подобрал такие преобразования между координатами и временем, чтобы они соответствовали экспериментальным данным,

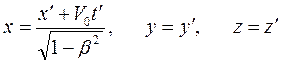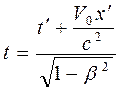, . (13.2)

Здесь 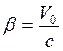, c = 3∙10⁸ м/с – скорость света в вакууме, V₀ – скорость переносной системы отсчета.

Для обратного перехода от подвижной системы отсчета к неподвижной достаточно поменять знак штриха и направление переносной скорости на противоположное. В уравнениях Лоренца перемешаны пространственные координаты и время. В этом проявляется взаимосвязь пространства и времени в теории относительности. При малых по сравнению со скоростью света скоростях (β <<1) преобразования Лоренца переходят в классические преобразования Галилея. Преобразования Лоренца, примененные к уравнениям Максвелла при переходе к другой системе отсчета, не меняют их вида.

На основании постулата постоянства скорости света Эйнштейн получил преобразования Лоренца. Пусть в начальный момент времени в общем начале координат обоих систем отсчета происходит вспышка света. Фронты световых волн в пространстве являются сферами. Уравнения координаты фронтов в направлении движения подвижной системы отсчета имеют вид 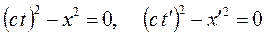. Предполагая линейную зависимость между координатами и временем, из этих уравнений были получены формулы преобразований Лоренца.