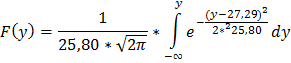Построить гистограмму и полигон относительных частот.

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Расчетно-графическая работа

Вариант № 1

Пояснительная записка

(СТ.231000.064.ПЗ)

Руководитель:

________ Т.Н.Логиновская

(подпись)

_________«___» _________2013г.

(оценка)

Выполнил:

Студент группы 21-06

________Д. В. Рулькевич

(подпись)

«_____» _______________2013г.

Красноярск, 2013

Задание:

Проводятся результаты 100 наблюдений над некоторой случайной двумерной величиной: (X, Y).

Требуется для каждой случайной величины X и Y (сокращенно СВ X и СВ Y):

1. Построить интервальный и дискретный статистический ряды распределения частот и относительных частот.

2. Построить гистограмму и полигон относительных частот.

3. Найти эмпирическую функцию распределения и построить её график.

4. Вычислить числовые характеристики выборки: выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, выборочные коэффициенты асимметрии и эксцесса.

5. Сделать предварительный выбор закона распределения наблюдаемой случайной величины, исходя из механизма её образования, по виду гистограммы и полигона относительных частот и по значениям выборочных коэффициентов асимметрии и эксцесса.

6. Найти точечные оценки параметров нормального закона распределения, предполагая, что наблюдаемая случайная величина распределена по нормальному закону, и записать функцию плотности распределения вероятностей.

7. Проверить с помощью критерия согласия Пирсона гипотезу о том, что выборка извлечена из генеральной совокупности с предполагаемым нормальным законом распределения.

8. В случае принятия гипотезы найти интервальные оценки параметров нормального закона распределения (доверительную вероятность принять равной 0,95).

9. Провести корреляционный анализ:

а) Составить корреляционную таблицу;

б) Найти выборочный коэффициент корреляции;

в) Проверить значимость выборочного коэффициента корреляции при
α = 0,05(Н₀ : ρ = 0), при альтернативной гипотезе Н_α: ρ ≠ 0;

г) Построить корреляционное поле и по характеру расположения точек на нём подобрать общий вид функции регрессии;

д) Найти эмпирические функции регрессии Y на X, X на Y и построить их графики.

Вариант № 1

№	X	№	X	№	X	№	X	№	X

Построить интервальный и дискретный статистический ряды распределения частот и относительных частот.

Сделаем группировку наблюдаемых значений. Оптимальную длину интервала определим по формуле Стэрджеса:

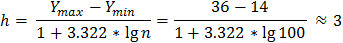
Таблица 1

Вспомогательная таблица для расчета числовых характеристик выборки

Интервалы (a(i);a(i+1)]	Середины интервалов	Подсчет частот	Частоты n(i)	Относит.частоты W(i)=n(i)/n	Накопленные Относит.частоты
(11,5;14,5]				0,02	0,02
(14,5;17,5]				0,06	0,08
(17,5;20,5]				0,17	0,25
(20,5;23,5]				0,19	0,44
(23,5;26,5]				0,21	0,65
(26,5;29,5]				0,2	0,85
(29,5;32,5]				0,11	0,96
(32,5;35,5]				0,03	0,99
(35,5;38,5]				0,01

Построить гистограмму и полигон относительных частот.

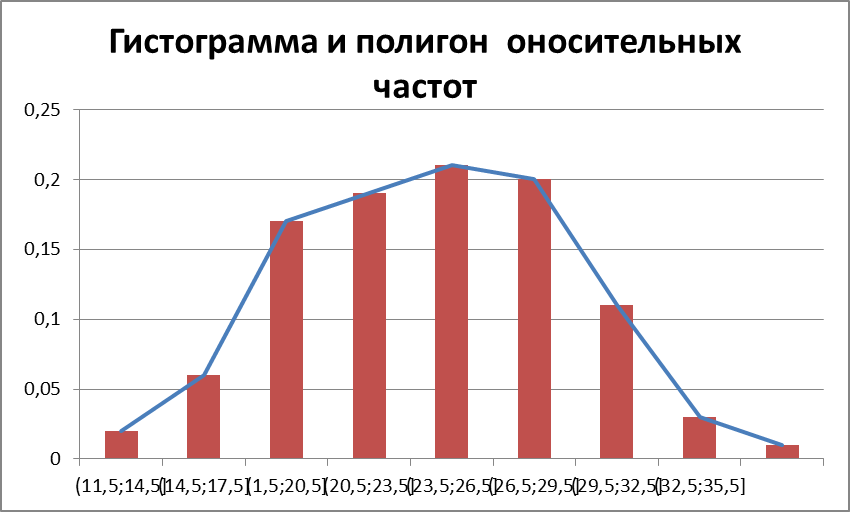
РИС. 1 Гистограмма и полигон относительных частот

3. Найти эмпирическую функцию распределения и построить её график.

	0,	если x <= 11,5
	0,08	если 11,5 <= x <=14,5
	0,25	если 14,5 <= x <= 17,5
	0,44	если 17,5 <= x<= 20,5
F(x)=	0,65	если 20,5 <= x <= 23,5
	0,85	если 23,5 <= x <= 26,5
	0,96	если 26,5 <= x <= 32,5
	0,99	если 32,5 <= x <= 35,5
		если 35,5 <= x <= 38,5

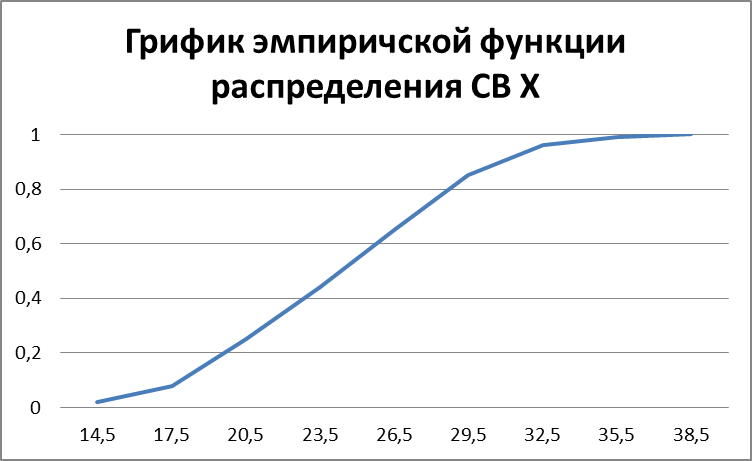
РИС. 2 График функции распределения

4. Вычислить числовые характеристики выборки: выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, выборочные коэффициенты асимметрии и эксцесса.

Таблица 2

Таблица для расчета числовых характеристик выборки

Середины интервалов y(i)	Частоты n(i)	y(i)-Y	(y(i)-Y)*n(i)	((y(i)-Y)^2)*n(i)	((y(i)-Y)^3)*n(i)	((y(i)-Y)^4)*n(i)
		-36,6	-73,20	2679,12	-98055,79	3588841,99
		-33,6	-201,60	6773,76	-227598,34	7647304,09
		-30,6	-520,20	15918,12	-487094,47	14905090,84
		-27,6	-524,40	14473,44	-399466,94	11025287,65
		-24,6	-516,60	12708,36	-312625,66	7690591,14
		-21,6	-432,00	9331,20	-201553,92	4353564,67
		-18,6	-204,60	3805,56	-70783,42	1316571,54
		-15,6	-46,80	730,08	-11389,25	177672,27
		-12,6	-12,60	158,76	-2000,38	25204,74
Сумма			-2532,00	66578,40	-1810568,16	50730128,93

Выборочное среднее (Y) даёт среднее значение мощности двигателя для данной

выборки.

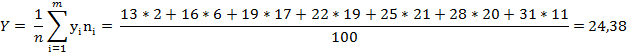
Выборочная дисперсия:

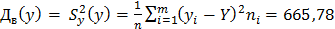
Выборочное среднее квадратичное отклонение:

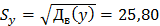
Выборочные коэффициенты асимметрии и эксцесса вычисляют по формулам:

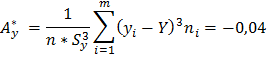
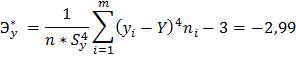
A_y – говорит о несимметричности полигона относительно выборочного среднего Y.

Э_у > 0, - это говорит о том, что полигон более крут, чем нормальная кривая.

5. Сделать предварительный выбор закона распределения наблюдаемой случайной величины, исходя из механизма её образования, по виду гистограммы и полигона относительных частот и по значениям выборочных коэффициентов асимметрии и эксцесса.

Вид полигона и гистограммы относительных частот напоминает нормальную кривую. Выборочные коэффициенты асимметрии и эксцесса для нормального распределения не более, чем на утроенные средние квадратичные ошибки их определения.

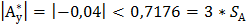
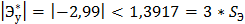
Где:

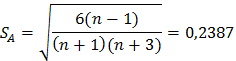
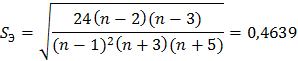
Итак, по совокупности указанных признаков можно предположить, что распределение СВ Y является нормальным.

Найти точечные оценки параметров нормального закона распределения, предполагая, что наблюдаемая случайная величина распределена по нормальному закону, и записать функцию плотности распределения вероятностей.

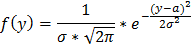
В качестве неизвестных параметров α и возьмем их точечные оценки Y и S_yсоответственно.

Функция плотности:

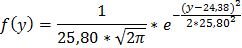
Функция распределения вероятности: