Предел функции нескольких переменных

Определение функции нескольких переменных. Основные понятия.

Если каждой паре независимых друг от друга чисел (х,у) из некоторого множества по какому-либо правилу ставится в соответствие одно значение переменной z, то она называется функцией двух переменных. z=f(x,y,)

Область определения функции z - совокупность пар (х,у), при которых функция z существует.

Множество значений (область значений) функции – все значения, которые принимает функция в ее области определения.

График функции двух переменных - множество точек P, координаты которых удовлетворяют уравнению z=f(x,y)

Окрестность точки M0 (х0;y0) радиуса r – совокупность всех точек (x,y), которые удовлетворяют условию 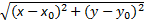< r

Область определения и область значений функции нескольких переменных. График функции нескольких переменных.

Предел и непрерывность функции нескольких переменных.

Предел функции нескольких переменных

Для того чтобы дать понятие предела функции нескольких переменных, ограничимся случаем двух переменных х и у. По определению функция f (x, y)имеет предел в точке (х₀, у₀), равный числу А, обозначаемый так:

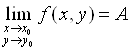(1)

(пишут еще f (x, y)→А при (x, y)→ (х₀, у₀)), если она определена в некоторой окрестности точки (х₀, у₀), за исключением, быть может, самой этой точки и если существует предел

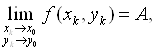(2)

какова бы ни была стремящаяся к (х₀, у₀) последовательность точек (x_k,y_k).

Так же, как в случае функции одной переменной, можно ввести другое эквивалентное определение предела функции двух переменных: функция f имеет в точке (х₀, у₀) предел, равный А, если она определена в некоторой окрестности точки (х₀, у₀) за исключением, быть может, самой этой точки, и для любого ε > 0 найдется такое δ > 0, что

| f (x, y) – A | < ε (3)

для всех (x, y), удовлетворяющих неравенствам

0 < 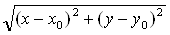< δ. (4)

Это определение, в свою очередь, эквивалентно следующему: для любого ε > 0 найдется δ-окрестность точки (х₀, у₀) такая, что для всех (x, y) из этой окрестности, отличных от (х₀, у₀), выполняется неравенство (3).

Так как координаты произвольной точки (x, y) окрестности точки (х₀, у₀) можно записать в виде х = х₀ + Δх, у = у₀ + Δу, то равенство (1) эквивалентно следующему равенству:

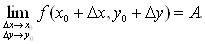
Рассмотрим некоторую функции, заданную в окрестности точки (х₀, у₀), кроме, быть может, самой этой точки.

Пусть ω = (ω_х, ω_у) – произвольный вектор длины единица (|ω|² = ω_х² + ω_у² = 1) и t > 0 – скаляр. Точки вида

(х₀ + tω_х, y₀ + tω_у) (0 < t)

образуют луч, выходящий из (х₀, у₀) в направлении вектора ω. Для каждого ω можно рассматривать функцию

f (х₀ + tω_х, y₀ + tω_у) (0 < t < δ)

от скалярной переменной t, где δ – достаточно малое число.

Предел этой функции (одной переменной t)

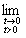f (х₀ + tω_х, y₀ + tω_у),

если он существует, естественно называть пределом f в точке (х₀, у₀) по направлению ω.

Пример 1. Функции

определены на плоскости (x, y) за исключением точки х₀ = 0, у₀ = 0. Имеем (учесть, что 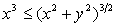и ):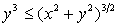

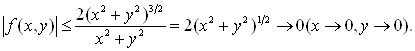
Отсюда

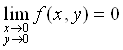
(для ε > 0 полагаем δ = ε/2 и тогда | f (x, y)| < ε, если 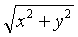< δ).

Далее, считая, что k – постоянная, имеем для y = kx равенство

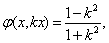
из которого видно, что предел φ в точке (0, 0) по разным направлениям вообще различен (единичный вектор луча y = kx, х > 0, имеет вид

).

Число А называется пределом функции f(M) при М → М₀, если для любого числа ε > 0 всегда найдется такое число δ > 0, что для любых точек М, отличных от М₀ и удовлетворяющих условию | ММ₀ | < δ, будет иметь место неравенство | f(M) – А | < ε.

Предел обозначают 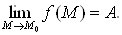В случае функции двух переменных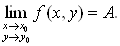

Теоремы о пределах. Если функции f₁(M) и f₂(M) при М → М₀ стремятся каждая к конечному пределу, то:

а)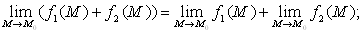

б)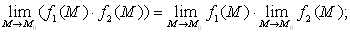

в)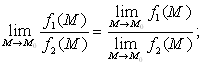

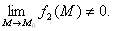
Непрерывность функции нескольких переменных

По определению функция f (x, y) непрерывна в точке (х₀, у₀), если она определена в некоторой ее окрестности, в том числе в самой точке (х₀, у₀) и если предел f (x, y) в этой точке равен ее значению в ней:

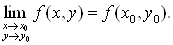(1)

Условие непрерывности f в точке (х₀, у₀) можно записать в эквивалентной форме:

(1")

т.е. функция f непрерывна в точке (х₀, у₀), если непрерывна функция f (х₀+ Δх, у₀ + Δу) от переменных Δх, Δу при Δх = Δу = 0.

Можно ввести приращение Δи функции и = f (x, y) в точке (x, y), соответствующее приращениям Δх, Δу аргументов

Δи = f (х + Δх, у + Δу) – f (x, y)

и на этом языке определить непрерывность f в (x, y): функция f непрерывна в точке (x, y), если

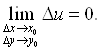(1"")

Теорема. Сумма, разность, произведение и частное непрерывных в точке (х₀,у₀) функций f и φ есть непрерывная функция в этой точке, если, конечно, в случае частного φ (х₀, у₀) ≠ 0.

Постоянную с можно рассматривать как функцию f (x, y) = с от переменных x,y. Она непрерывна по этим переменным, потому что

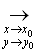| f (x, y) – f (х₀, у₀) | = |с – с | = 0 0.

Следующими по сложности являются функции f (x, y) = х и f (x, y) = у. Их тоже можно рассматривать как функции от (x, y), и при этом они непрерывны. Например, функция f (x, y) = х приводит в соответствие каждой точке (x, y)число, равное х. Непрерывность этой функции в произвольной точке (x, y)может быть доказана так:

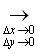| f (х + Δх, у + Δу) – f (x, y) | = | f (х + Δх) – х | = | Δх | ≤ 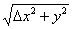0.

Если производить над функциями x, y и постоянными действия сложения, вычитания и умножения в конечном числе, то будем получать функции, называемые многочленами от x, y. На основании сформулированных выше свойств многочлены от переменных x, y – непрерывные функции от этих переменных для всех точек (x, y) 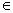R₂.

Отношение P/Q двух многочленов от (x, y) есть рациональная функция от (x,y), очевидно, непрерывная всюду на R₂, за исключением точек (x, y), где Q(x, y) = 0.

Функция

Р (x, y) = х³ – у² + х²у – 4

может быть примером многочлена от (x, y) третьей степени, а функция

Р (x, y) = х⁴ – 2х²у² + у⁴

есть пример многочлена от (x, y) четвертой степени.

Приведем пример теоремы, утверждающей непрерывность функции от непрерывных функций.

Теорема. Пусть функция f (x, y, z) непрерывна в точке (x₀, y₀, z₀)пространства R₃ (точек (x, y, z)), а функции

x = φ (u, v), y = ψ (u, v), z = χ (u, v)

непрерывны в точке (u₀, v₀) пространства R₂ (точек (u, v)). Пусть, кроме того,

x₀ = φ (u₀, v₀), y₀= ψ (u₀, v₀), z₀= χ (u₀, v₀).

Тогда функция F (u, v) = f [ φ (u, v), ψ (u, v), χ (u, v) ] непрерывна (по

(u, v)) в точке (u₀, v₀).

Доказательство. Так как знак предела можно внести под знак характеристики непрерывной функции, то

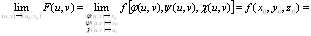
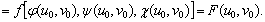
Теорема. Функция f (x, y), непрерывная в точке (х₀, у₀) и не равная нулю в этой точке, сохраняет знак числа f (х₀, у₀) в некоторой окрестности точки (х₀, у₀).

По определению функция f (x) = f (x₁, ..., х_п) непрерывна в точке х⁰ =(х⁰₁, ..., х⁰_п), если она определена в некоторой ее окрестности, в том числе и в самой точке х⁰, и если предел ее в точке х⁰ равен ее значению в ней:

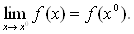(2)

Условие непрерывности f в точке х⁰ можно записать в эквивалентной форме:

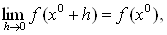(2")

т.е. функция f (x) непрерывна в точке х⁰, если непрерывна функция f (х⁰ +h) от h в точке h = 0.

Можно ввести приращение f в точке х⁰, соответствующее приращению h = (h₁, ..., h_п),

Δ_h f (х⁰) = f (х⁰ + h) – f (х⁰)

и на его языке определить непрерывность f в х⁰: функция f непрерывна в х⁰, если

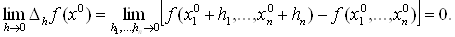(2"")

Теорема. Сумма, разность, произведение и частное непрерывных в точке х⁰функций f (x) и φ (x) есть непрерывная функция в этой точке, если, конечно, в случае частного φ (х⁰) ≠ 0.

Замечание. Приращение Δ_h f (х⁰) называют также полным приращением функцииf в точке х⁰.

В пространстве R_n точек х = (x₁, ..., х_п) зададим множество точек G.

По определению х⁰ = (х⁰₁, ..., х⁰_п) есть внутренняя точка множества G, если существует открытый шар с центром в нем, полностью принадлежащий к G.

Множество G 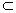R_n называется открытым, если все его точки внутренние.

Говорят, что функции

х₁ = φ₁ (t), ..., х_п = φ_п (t) (a ≤ t ≤ b)

непрерывные на отрезке [a, b], определяют непрерывную кривую в R_n, соединяющую точки х¹ = (х¹₁, ..., х¹_п) и х² = (х²₁, ..., х²_п), где х¹₁ = φ₁(а), ..., х¹_п = φ_п (а), х²₁ = φ₁ (b), ..., х²_п = φ_п (b). Букву t называют параметром кривой.

Множество G называется связным, если любые его две точки х¹, х² можно соединить непрерывной кривой, принадлежащей G.

Связное открытое множество называется областью.

Теорема. Пусть функция f (x) определена и непрерывна на R_n (во всех точкахR_n). Тогда множество G точек х, где она удовлетворяет неравенству

f (x) > с (или f (x) < с), какова бы ни была постоянная с, есть открытое множество.

В самом деле, функция F(x) = f(x) – с непрерывна на R_n, и множество всех точек х, где F(x) > 0, совпадает с G. Пусть х⁰ 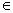G, тогда существует шар

| х – х⁰ | < δ,

на котором F(x) > 0, т.е. он принадлежит к G и точка х⁰ 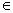G – внутренняя для G.

Случай с f (x) < с доказывается аналогично.

Таким образом, функция нескольких переменных f (М) называется непрерывной в точке М₀, если она удовлетворяет следующим трем условиям:

а) функция f (М) определена в точке М₀ и вблизи этой точки;

б) существует предел ;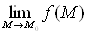

в)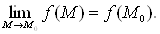

Если в точке М₀ нарушено хотя бы одно из этих условий, то функция в этой точке терпит разрыв. Точки разрыв могут образовывать линии разрыва, поверхность разрыва и т. д. Функция f (М) называется непрерывной в областиG, если она непрерывна в каждой точке этой области.

Пример 1. Найти точки разрыва функции: z = ln (x² + y²).

Решение. Функция z = ln (x² + y²) терпит разрыв в точке х = 0, у = 0. Следовательно, точка О (0, 0) является точкой разрыва.