Краткие теоретические и учебно-методические материалы

По теме практического занятия

Множество – совокупность объектов любой природы ,обладающих общим свойством.

Элементы множества –объекты, составляющие множество.

Множества обозначают заглавными латинскими буквами: A, B, C,… , а элементы множества – а, b, c, d,…

Множество называется заданным, если или перечислены все его элементы, или указано свойство, которым обладают те и только те элементы, которые принадлежат данному множеству.

Конечное множество –множество, которое содержит конечное число элементов. Число элементов конечного множества называется мощностьюмножества А и обозначается m(А).

В противном случае, множество называется бесконечным.

Пустое множество –множество, не содержащее ни одного элемента, и обозначается .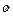

A и B называются равными, если все х, принадлежащие А, принадлежат В и все х, принадлежащие В, принадлежат А.

Множество В называется подмножеством множества А, если любые элементы х из множества В принадлежат множеству А: .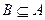

Существуют 3 способа задания множества:1) Перечислением его элементов. Так

можно задать только конечные множества. Пример. А =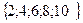

2) Описанием характеристических свойств, которыми обладают его элементы

Пример. А = 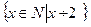- множество натуральных чисел, делящихся на 2.

3) Порождающей процедурой, которая описывает способ получения элементов множества из уже имеющихся элементов либо другихобъектов.

В этом случае элементами множества являются все объекты, которые могут быть построены с помощью такой процедуры.

Универсальным множеством U называется множество всех элементов, которые

могут встретиться в данном исследовании.

Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Если А, В – конечные множества, то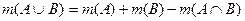

Основные тождества.

Для любых подмножеств А, В, С иуниверсального множества U выполняются следующие тождества:

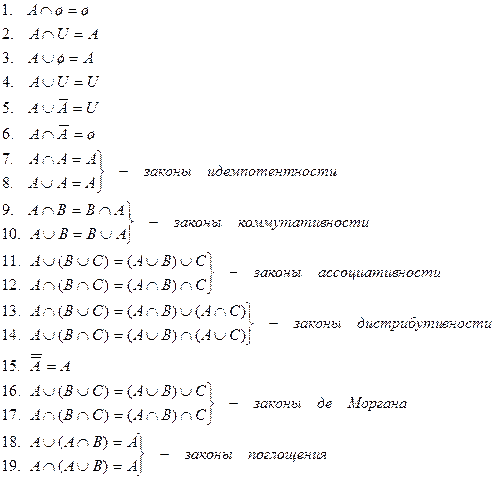
Вопросы для закрепления теоретического материала к практическому занятию

1. Что собой представляет множество?

2. Что называется элементом множества?

3. Какие виды множеств вы знаете?

4. Что называется объединением множеств?

5. Что называется пересечением множеств?

7. Что называется разностью и симметрической разностью множеств?

8. Что понимают под дополнением множества А?

9. Что собой представляет текстовая задача?

10.Что собой представляет собой диаграмма Эйлера-Венна?

Практическое занятие № 3

«Решение задач на применение множеств и кругов Эйлера»

1. Доказать с помощью кругов Эйлера тождество.

2. Найти множества .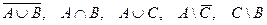

3. Записать множество, перечислив его элементы.

4. Перечислить элементы множества А.

5. Решить задачу.

Вариант	Задание 1	Задание 2

.

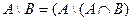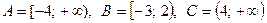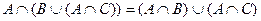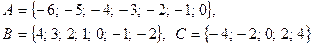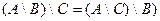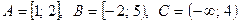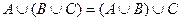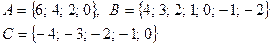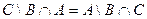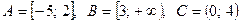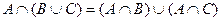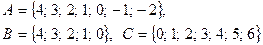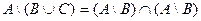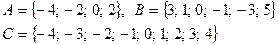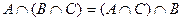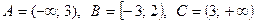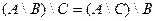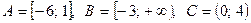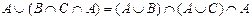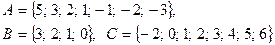Вариант	Задание 3
	Множество всех положительных чисел, кратных 9, которые меньше 80
	Множество всех целых положительных степеней числа 5 меньших 630
	Множество всех положительных простых чисел, меньших 30
	Множество всех положительных чётных чисел
	Множество всех отрицательных чётных чисел
	Множество корней уравнения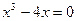
	Множество натуральных чисел, меньших 7
	Множество чётных чисел, меньших 10
	Множество нечётных чисел, больших 1
	Множество целых чисел, делящихся на 2

Вариант	Задание 4

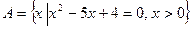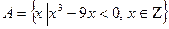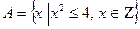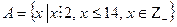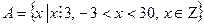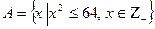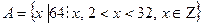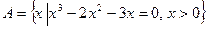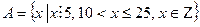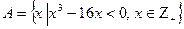Задание 5.

Вариант 1. На одну специальность в одном из ВУЗов поступало 120 человек. Абитуриенты сдавали три экзамена: по математике, по информатике и русскому языку. Математику сдали 60 человек, информатику - 40. 30 абитуриентов сдали математику и информатику, 30 - математику и русский язык, 25 - информатику и русский язык. 20 человек сдали все три экзамена, а 50 человек - провалили. Сколько абитуриентов сдали русский язык?

Вариант 2.Каждый студент в группе изучает либо английский, либо французский язык, либо оба этих языка. Английский язык изучают 25 человек, французский — 27 человек, а тот и другой —18 человек. Сколько всего студентов в группе?

Вариант 3. Каждый из членов команды играет либо в футбол, либо в хоккей, либо в футбол и в хоккей. Сколько человек в команде, если известно, что 18 человек играют в обе игры, 23 человека играют в футбол, 21 – в хоккей?

Вариант 4.В лицее при некотором университете 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке – 8, 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке?

Вариант 5.Среди прохожих провели опрос. Был задан вопрос: "Какое домашнее животное у Вас есть?". По результатам опроса выяснилось, что у 150 человек есть кошка, у 130 - собака, у 50 - птичка. У 60 человек есть кошка и собака, у 20 - кошка и птичка, у 30 - собака и птичка. У 70 человек вообще нет домашнего животного. У 10 человек есть и кошка, и собака, и птичка. Сколько прохожих приняли участие в опросе?

Вариант 6.В группе 36 студентов. Многие из них посещают круж­ки: физический (14 человек), математический (18 чело­век), химический (10 человек). Кроме того, известно, что 2 человека посещают все три кружка; из тех, кто по­сещает два кружка, 8 человек занимаются в математи­ческом и физическом кружках, 5 — в математическом и химическом, 3 — в физическом и химическом. Сколь­ко человек не посещают никаких кружков?

Вариант 7. В группе из 100 туристов 66 человек знают английский язык, 54 знают французский язык и 33 человека знают оба языка.

Сколько туристов в группе, не знают ни английского, ни французского языков?

Вариант 8. На олимпиаде по физике студентам предложили решить три задачи: одну по кинематике, одну по термодинамике, одну по оптике. Результаты олимпиады были следующие: задачу по кинематике решили 400 участников, по термодинамике - 350, по оптике - 300. 300 студентов решили задачи по кинематике и термодинамике, 200 - по кинематике и оптике, 150 - по термодинамике и оптике. 100 человек решили задачи по кинематике, термодинамике и оптике. Сколько студентов решило две задачи?

Вариант 9. В группе из 40 ребят 30 умеют плавать, 27 умеют играть в шахматы и только пятеро не умеют ни того, ни другого.

Сколько человек умеющих плавать и играть в шахматы?

Вариант 10. На олимпиаде по математике студентам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 студентов. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии - 700, по тригонометрии - 600. 600 студентов решили задачи по алгебре и геометрии, 500 - по алгебре и тригонометрии, 400 - по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько студентов не решило ни одной задачи?