Свободные колебания без учета сил сопротивления

Лекция 3. Прямолинейные колебания точки

В данной лекции рассматриваются следующие вопросы:

1. Свободные колебания без учета сил сопротивления.

2. Сложение колебаний.

3. Энергия гармонических колебаний.

4. Понятие о фазовой плоскости.

5. Свободные колебания в поле постоянной силы.

6. Параллельное включение упругих элементов.

7. Последовательное включение упругих элементов.

8. Вынужденные колебания. Резонанс.

9. Свободные колебания с вязким сопротивлением.

10. Вынужденные колебания с вязким сопротивлением.

Изучение данных вопросов необходимо для динамики колебательного движения механических систем, теории удара, для решения задач в дисциплинах «Сопротивление материалов» и «Детали машин».

Свободные колебания без учета сил сопротивления.

Движения, обладающие той или иной степенью повторяемости, называются колебаниями.

Колебания свойственны всем явлениям природы: пульсирует излучение звезд, с высокой степенью периодичности вращаются планеты Солнечной системы, в земной ионосфере и атмосфере циркулируют потоки заряженных частиц, ветры возбуждают колебания воды на поверхности водоемов. Внутри любого живого организма непрерывно происходят разнообразные, ритмично повторяющиеся процессы, например, с удивительной надежностью бьется сердце, даже психика людей подвержена колебаниям. В виде сложнейшей совокупности колебаний частиц и полей можно представить «устройство» микромира.

В технике колебания либо выполняют определенные функциональные обязанности (маятник, колебательный контур, генератор), либо возникают как неизбежное проявление физических свойств (вибрация машин и сооружений, неустойчивости и вихревые потоки при движении тел в газах).

В физике выделяются колебания механические, электромагнитные и их комбинации. Это обусловлено той исключительной ролью, которую играют гравитационные и электромагнитные взаимодействия в масштабах, характерных для жизнедеятельности человека. С помощью распространяющихся механических колебаний плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых колебаний электрических и магнитных полей, воспринимаемых нами как свет, мы получаем бóльшую часть прямой информации об окружающем нас мире.

По мере изучения колебаний различной физической природы возникло убеждение о возможности общего, «внепредметного» подхода к ним, основанного на свойствах и закономерностях колебательных процессов вообще. В результате появилась теория колебаний и волн. Основным математическим аппаратом теории колебаний являются дифференциальные уравнения.

Хотя колебания, рассматриваемые в различных областях, на­пример в механике, радиотехнике, акустике и др., отличаются друг от друга по своей физической природе, основные законы этих коле­баний во всех случаях остаются одними и теми же. Поэтому изуче­ние механических колебаний является важным не только по той причине, что такие колебания очень часто имеют место в технике, но и вследствие того, что результаты, полученные при изучении меха­нических колебаний, могут быть использованы для изучения и уясне­ния колебательных явлений в других областях.

Если значения физических величин, изменяющихся в процессе движения, повторяются через равные промежутки времени, то такое движение называется периодическим. Примерами периодического движения могут служить движение планет вокруг Солнца, движение поршня в цилиндре двигателя внутреннего сгорания и др. В зависимости от физической природы колебательного процесса и «механизма» его возбуждения различают механические и электромагнитные колебания. Колебательную систему вне зависимости от ее физической природы называютосциллятором. Примером осциллятора может служить колеблющийся груз, подвешенный на пружине или нити.

Полным колебаниемназывают один законченный цикл колебательного движения, после которого оно повторяется в том же порядке.

По способу возбуждения колебания делят на: свободные(собственные), происходящие в представленной самой себе системе около положения равновесия после какого-либо первоначального воздействия; вынужденные – происходящие при периодическом внешнем воздействии (например, колебания моста при прохождении по нему поезда или раскачивание человеком качелей); параметрические– происходящие при изменении какого-либо параметра колебательной системы; автоколебания– происходящие в системах, самостоятельно регулирующих поступление внешних воздействий.

Собственные колебания являются не только самыми распространенными, но и самыми важными с точки зрения теории колебаний, так как условия возникновения и характер всех других типов колебаний существенно зависят от характера собственных колебаний.

Начнем с изучения свободных колебаний точки без учета сил сопротивления. Рассмотрим точку М, движущуюся прямолинейно под действием одной только восстанавливающей силы 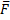, направленной к неподвижному центру О и пропорциональной расстоянию от этого центра. Проекция силы 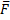на ось Ох (рис.1) будет равна

F_x=-cx.

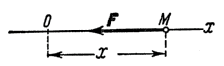
Рис.1

Сила 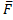, как видим, стремится вернуть точку в равновесное положение О, где F=0; отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости. Коэффициент c пропорциональности называется жесткостью упругого элемента.

Любая другая сила, неупругая по природе, но удовлетворяющая соотношению F = – cx, называется квазиупругой.

Найдем закон движения точки М. Составляя дифференциальное уравнение движения получим

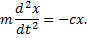
Деля обе части равенства на т и вводя обозначение

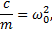
приведем уравнение к виду

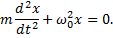
Уравнение представляет собою дифференциальное уравне­ние свободных колебаний при отсутствии сопротивления. Реше­ние этого линейного однородного дифференциального уравнения второго порядка ищут в виде x=e^nt. Полагая x=e^nt, получим для определения п так называемое характеристиче­ское уравнение, имеющее в данном случае вид п² + 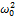= 0. Поскольку корни этого характеристического уравнения являются чисто мнимыми ( 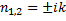), то, как известно из теории дифференциальных уравне­ний, общее решение имеет вид

X=C₁sinω₀t+C₂cosω₀t,

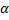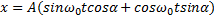где C₁ и С₂ - постоянные интегрирования. Если вместо постоянных C₁ и С₂ ввести постоянные а и , такие, что , то мы получим или .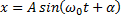

Это другой вид решения, в котором постоянными интегрирования являются A и 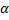. Им удобнее пользоваться для общих исследований.

Скорость точки в рассматриваемом движении равна

.

Несмотря на большое разнообразие колебательных процессов, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими.

Колебания, совершаемые точкой по закону косинуса или синуса 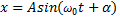или 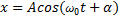называются гар­моническими колебаниями.

Система, закон движения которой имеет такой вид, называется одномерным (линейным) классическим гармоническим осциллятором или сокращенно гармоническим осциллятором.

Скорость и ускорение гармонического осциллятора находят, взяв первую, а затем вторую производные от смещения x:

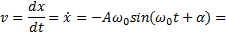
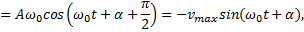
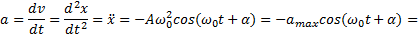
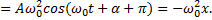
Тогда сила

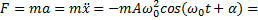
Этот вид колебаний особенно важен по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническим; во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.

Всем характеристикам этого движения можно дать наглядную ки­нематическую интерпретацию. Рассмотрим точку В, движущуюся равномерно по окружности радиуса а из положения В₀ определяемого углом 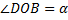(рис.2).

Пусть постоянная угловая ско­рость вращения радиуса ОВ равна 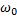. Тогда в произвольный момент времени t угол 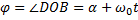и про­екция М точки В на диаметр, перпендику­лярный к DE, движется по закону 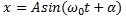, где х=ОМ, т.е. совер­шает гармонические колебания.

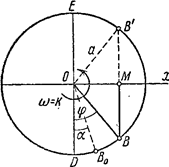
Рис.2

Величина A, равная наибольшему откло­нению точки М от центра колебаний, назы­вается амплитудой колебаний. Величина 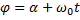называется фазой колебаний.

Фаза колебания определяет смещение в момент времени t. Начальная фаза α определяет смещение тела в момент начала отсчета времени.

Фаза колебаний представляет собой угловую меру времени, прошедшего от начала колебаний.

Колебания точки, происходящие с постоянной амплитудой, называютнезатухающими,а колебания с постепенно уменьшающейся амплитудой – затухающими.

Величина k, совпадающая с угловой скоростью вращения радиуса ОВ, показанного на рис.2 называется круговой (круговой) частотой колебаний.

Циклической иликруговой частотой периодических колебаний называется число полных колебаний, совершаемых за время 2π с:

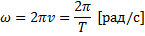
Промежуток времени Т (или 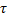), в течение которого точка совер­шает одно полное колебание, называется периодом колебаний.

По истечении периода фаза изменяется на 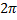. Следовательно, должно 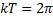откуда период

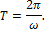
Величина 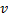, обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний

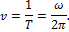
Отсюда видно, что величина k отличается от Т только постоянным множителем 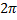. В дальнейшем мы обычно для краткости частотой колебаний будем называть величину k.

Единица частоты колебаний — герц (Гц). Герц – это частота колебаний, период которых равен 1 с: 1 Гц = 1 с ^–1.

Если положение тела в любой момент времени может быть описано единственным параметром, то тело имеет одну степень свободы. Такое колеблющееся тело называют одномерным осциллятором.

Значения A и 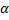определяются по начальным условиям. Считая при t=0 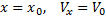получим 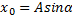и 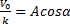. Отсюда, складывая сначала квадраты этих равенств,а затем деля их почленно, найдем:

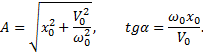
Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами: 1) амплитуда и начальная фаза колебаний зависят от начальных условий; 2) частота k, а следова­тельно, и период Т колебаний от начальных условий не зависят.

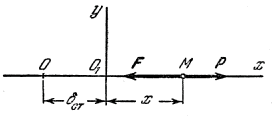
Рис.3

Влияние постоянной силы на свободные колебания точки. Пусть на точку М, кроме восстанавливающей силыF,направленной к центру О, действует еще постоянная по модулю и направлению сила Р (рис.3). Ве­личина силы F по прежнему пропорциональна расстоянию от центра О, т.е. .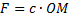

Очевидно, что в этом случае положением рав­новесия точки М будет центр О₁ отстоящий от О на расстоянии 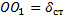, которое определяется равенством 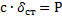или

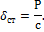
Величину 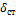назовем статическим отклонением точки. Примем центр O₁ за начало отсчета и направим координатную ось О₁х в сторону действия силы 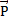. Тогда 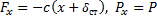. В результате, составляя дифференциальное уравнение дви­жения и учитывая, что согласно равенству 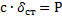, будем иметь:

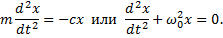
Отсюда заключаем, что постоянная сила Р не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы F, а только смещает центр этих колебаний в сторону действия силы Р на величину ста­тического отклонения .

Физический маятник. Представляет собой твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр масс (центр тяжести) тела (рис.4).

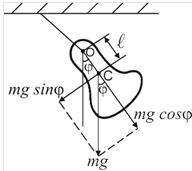
Рис.4

Колебания маятника, как и в случае математического маятника, совершаются под действием силы тяжести:

mgsinφ≈mgφ

Если маятник отклонить на некоторый угол j от положения равновесия, то на него будет действовать момент силы:

M=mgsinφl

(или для малых углов M=mgφl), возвращающий его в исходное положение, где l – расстояние от точки подвеса О до центра тяжести маятника – С.

Воспользовавшись основным уравнением динамики вращательного движения 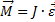, запишем уравнение колебаний физического маятника:

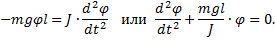
Решением этого уравнения является выражение вида

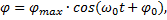
где 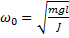- частота собственных колебаний маятника.

Таким образом, маятник будет совершать гармонические колебания, период которых определяется выражением

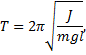
Приведенная длина физического маятника (l_пр) – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника:

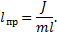
Математический маятник. Это модель, в которой вся масса сосредоточена в материальной точке, колеблющейся на невесомой и недеформируемой нити по дуге окружности в вертикальной плоскости под действием силы тяжести (рис. 5).

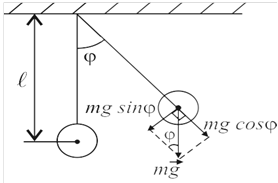
Рис.5

Момент силы, действующей на маятник равен,

M= -mglsinφ.

Знак « – » указывает, что момент силы противоположен направлению поворота. Так как угол φ мал, то sinφ≈φ и M= -mglφ.

Основное уравнение динамики для вращающегося тела имеет вид

,

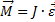Для математического маятника момент инерции J=ml², а угловое ускорение 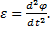Тогда как уравнение движения математического маятника запишется

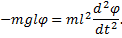
Перепишем это уравнение в следующем виде:

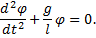
Мы получили дифференциальное уравнение второго порядка, решением которого является

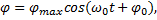
где частота собственных колебаний маятника 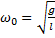, т.е. период собственных колебаний равен

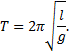
Выражение определено только для малых углов φ.

Пружинный маятник. Это система, состоящая из груза массы m, прикрепленного к пружине, массой которой можно пренебречь по сравнению с массой груза.

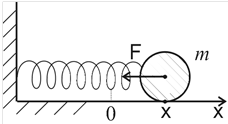
Рис.6

При малом смещении шарика вправо относительно положения равновесия (рис.6) на него действует возвращающая сила F – сила упругости, пропорциональная смещению х и направленная к положению равновесия:

F=-kx,

где k – коэффициент упругости [Н/м].

Уравнение движения пружинного маятника определяется вторым законом Ньютона:

F=ma.

Так как 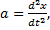то уравнение движения шарика примет вид

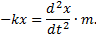
Преобразуем это уравнение:

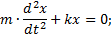
или

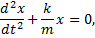
где 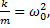ω₀ - круговая частота собственных колебаний.

Следовательно, период собственных колебаний пружинного маятника будет определяться выражением

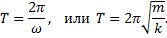
Запишем общий вид дифференциального уравнения гармонических колебаний:

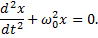
Решением этого уравнения является функция x=Acos(ω₀t+φ₀), что можно проверить подстановкой. График x(t) приведен на рисунке 6.1.

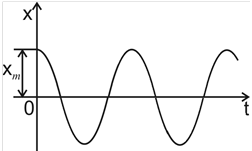
Рис.6.1

Свойствами маятников широко пользуются в различных приборах (в часах, в приборах для определения ускорения свободного падения, ускорений движущихся тел, колебаний земной коры, в гироскопических устройствах, в приборах для экспериментального определения момента инерции тел).

Сложение колебаний

Векторная диаграмма колебаний.Решение многих вопросов, в том числе сложение нескольких колебаний одного и того же направления, значительно облегчается и становится наглядным, если изображать колебания графически в виде векторов на плоскости (рис.7).

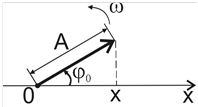
Рис.7

Если привести этот вектор во вращение с угловой скоростью w, то проекция конца вектора будет перемещаться по оси х в пределах от +А до –А, причем координата этой проекции будет изменяться со временем по закону:

x=Acos(ωt+φ₀).

Следовательно, гармоническое колебание может быть задано с помощью вращающегося вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью х угол φ, равный начальной фазе колебания. Вращение вектора х может быть задано уравнением

φ(t)=φ₀+ωt.

Сложение колебаний одного направления. Биения.Возможны случаи, когда тело участвует одновременно в нескольких колебательных процессах, происходящих вдоль одного и того же направления. Например, шарик, подвешенный на пружине к потолку вагона, качающегося на рессорах, участвует в собственных колебаниях относительно вагона и в колебаниях вагона относительно Земли. Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты, но с различными начальными фазами и амплитудами:

x₁=A₁cos(ωt+φ₁),

x₂=A₂cos(ωt+φ₂). (1)

Представим оба колебания на векторной диаграмме и построим по правилам сложения векторов результирующий вектор 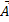(рис. 7.1).

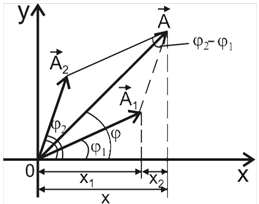
Рис.7.1

Так как проекция 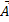на ось х равна сумме проекций слагаемых векторов, следовательно, вектор 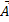представляет собой результирующее гармоническое колебание той же частоты ω, с амплитудой А и начальной фазой φ. Из построения видно, что по теореме косинусов можно записать:

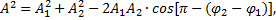
или

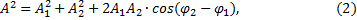
и

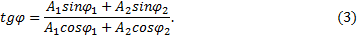
Итак, при сложении двух гармонических колебаний одинаковой частоты, направленных по одной и той же прямой, результирующее движение – также гармоническое колебание с той же частотой ω и с амплитудой А, лежащей в пределах

(A₁-A₂)≤A≤(A₁+A₂). (4)

Если фазы обоих колебаний одинаковы φ₂=φ₁, то амплитуды колебаний просто складываются A=A₁+A₂.

Если φ₂-φ₁=π, то колебания находятся в противофазе, и A=|A₁-A₂|, в частности, если A₁=A₂, то A=0, т.е. оба колебания взаимно уничтожаются.

Биениями называют периодические изменения амплитуды колебаний, возникающие при сложении двух гармонических колебаний с близкими частотами (рис.7.2) (T – период биения).

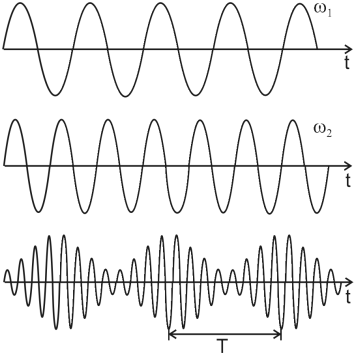
Рис. 7.2

Биение возникает вследствие того, что разность фаз между двумя колебаниями с различными частотами все время изменяется так, что оба колебания оказываются в какой-то момент времени в фазе, через некоторое время – в противофазе, затем снова в фазе и т.д. Если А₁ и А₂ – амплитуды двух накладывающихся колебаний, то при одинаковых фазах колебаний амплитуда достигает наибольшего значения A=A₁+A₂, а когда фазы колебаний противоположны, амплитуда падает до наименьшего значения A₁-A₂. В простейшем случае, когда амплитуды обоих колебаний равны, их сумма достигает значения 2А при одинаковых фазах колебаний и падает до нуля, когда они противоположны по фазе.

Результат наложения колебаний можно записать в виде

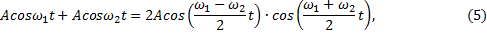
где ω₁ и ω₂ - циклические частоты двух накладывающихся гармонических колебаний.

Если ω₁ и ω₂ мало различаются, то величину 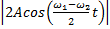в уравнении (5) можно рассматривать как медленно меняющуюся амплитуду (огибающую) колебания, происходящего по закону

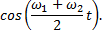
Частота Ω=ω₁-ω₂ называется циклической частотой биений.

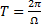- период биений.

По мере сближения частот ω₁ и ω₂ частота биения Ω уменьшается, исчезая при ω₁ → ω₂ («нулевые» биения). Определение частоты биения между измеряемым и эталонным колебаниями – один из наиболее точных методов измерения частоты, широко применяемый на практике. Метод биений применяют для измерения емкости, индуктивности, для настройки музыкальных инструментов, при анализе слухового восприятия и т.д.

Сложение взаимно перпендикулярных колебаний.Рассмотрим систему, обладающую двумя степенями свободы, т.е. такую систему, для задания положения которой нужны две координаты.

На рисунке 8 тяжелый шарик, подвешенный на легкой длинной пружине, совершает маятникообразные колебания в одной плоскости. Если растянуть и отпустить пружину, то шарик будет двигаться по некоторой сложной траектории, участвуя в двух колебаниях.

На рисунке 8.1 показан тяжелый шарик, подвешенный на длинной тонкой нити. Этот шарик может совершать одновременно колебания во взаимноперпендикулярных направлениях, причем частоты колебаний одинаковы, в этом случае вид колебаний будет зависеть от разности фаз обоих колебаний.

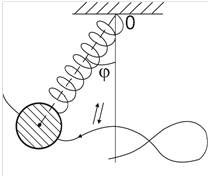
Рис.8

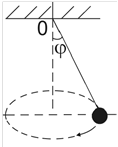
Рис.8.1

Рассмотрим результат сложения взаимно перпендикулярных гармонических колебаний одной и той же частоты w, совершающихся вдоль координатных осей х и у. Уравнения этих колебаний запишутся следующим образом:

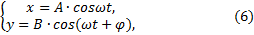
где φ – разность фаз колебаний.

Чтобы получить уравнение траектории точки, нужно исключить из этих уравнений параметр t. Из первого уравнения следует, что

тогда с учетом, что sin²ωt+cos²ωt=1, можно записать

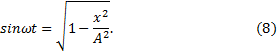
Преобразуем второе уравнение (6):

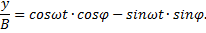
Подставим sinωt и cosωt (7) и (8) и избавимся от корня:

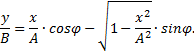
Возведем обе части равенства в квадрат:

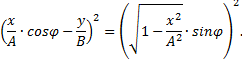
После преобразования имеем

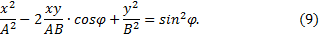
Как известно из аналитической геометрии, полученное уравнение является уравнением эллипса, ориентация и значение полуосей которого относительно осей х и у зависит от амплитуд А и В и разности фаз φ. Исследуем форму траектории в некоторых частных случаях.

1. φ=0. В этом случае уравнение примет вид

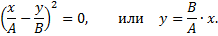
Это уравнение прямой, следовательно, в этом случае точка движется по прямой (рис. 8.2).

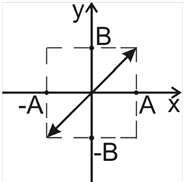
Рис.8.2

2. φ=±π. Уравнение траектории примет вид

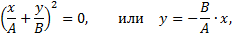
т.е. в этом случае точка гармонически колеблется вдоль прямой (рис.8.3).

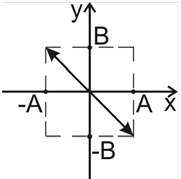
Рис.8.3

3. При φ=± 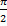уравнение траектории примет вид

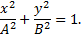
Это уравнение эллипса, полуоси которого равны соответствующим амплитудам колебаний. Если А = В, эллипс вырождается в окружность; при 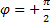движение происходит по часовой стрелке, при 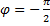точка движется по эллипсу против часовой стрелки (рис. 8.4).

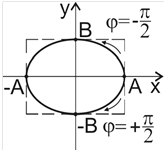
Рис.8.4

Фигуры Лиссажу.Если частоты двух взаимно перпендикулярных колебаний неодинаковы, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу (таблица 1).

Метод фигур Лиссажу – широко распространенный способ сравнения (измерения) частот двух складываемых колебаний, т.к. отношение частот обратно пропорционально количеству точек касания кривой с соответствующей осью:

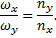
Таблица 1

Отношение nx/ny	φ = 0	π/4	π/2	3π/4	π
1:1
1:2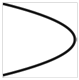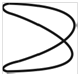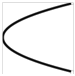
1:3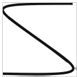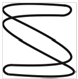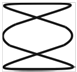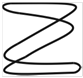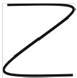
2:3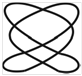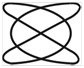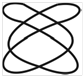
3:4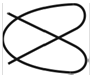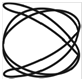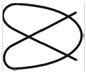