Способи задання булевих функцій

Довільна булева функція може бути задана одним із трьох способів: геометричним, табличним і аналітичним.

При геометричному способі булева функція задається за допомогою n-вимірного кубу. У цьому випадку, набори значень аргументів називають часто називають точками, оскільки кожний із них може бути ототожнений із певною вершиною одиничного n-вимірного кубу. Наприклад, для n=1, n=2 і n=3 ці куби подано на рис.1.

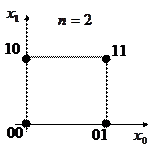
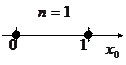Рис. 1

Легко бачити, що булева функція від n змінних визначена на множині, яка складається з 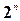двійкових наборів значень цих змінних. Зокрема, при n=1 таких наборів 2¹=2: – 0 і 1; при n=2 таких наборів вже 2²=4: – 00, 01, 10 і 11; при n=3 таких наборів 2³=8: 000, 001, 010, 011, 100, 101, 110 і 111 і т.д.

Скінченність області визначення та області значень булевих функцій дає можливість задавати їх за допомогою таблиць, які називаються таблицями істинності.

Надалі будемо розглядати двійкові набори значень змінних як значення деяких цілих чисел у двійковій системі числення так, що набір 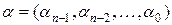будемо ототожнювати із записом цілого десяткового числа вигляду

.

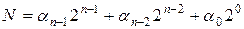Назвемо це число десятковим номером відповідного двійкового набору. Так, наприклад, для чотиримісної (n=4) булевої функції номером набору 1001 є десяткове число

.

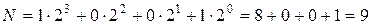Номери наборів n­-­мі­сної булевої функції змінюються від 0 до 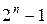. Розташувавши набори стовпчиком у порядку зростання їх номерів і поклавши значення функції проти кожного набору, одержимо таблицю істинності булевої функції (табл. 1).

Таблиця 1

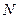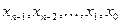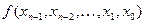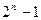…	0, 0, … ,0, 0 0, 0, … ,0, 1 0, 0, … ,1, 0 0, 0, … ,1, 1 …………… 1, 1, … ,1, 1	F(0, 0, … ,0, 0) F(0, 0, … ,0, 1) F(0, 0, … ,1, 0) F(0, 0, … ,1, 1) ……………… F(1, 1, … ,1, 1)

У зв’язку з тим, що на кожному наборі булева функція може приймати одне з двох значень (0 або 1) незалежно від значень, що вона приймає на інших наборах, існують 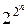різних n­-­мі­сних булевих функцій.

В табл. 2-3 наведено приклади табличного задання повністю заданої

функції від трьох змінних, а в табл. 4 – неповністю заданої функції від такої самої кількості змінних.

Розглянутий спосіб задання функції прийнято для функції невеликої кількості змінних, оскільки зі збільшенням кількості змінних (п) кількість наборів збільшиться як 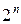і таблиця істинності стає громіздкою.

Більш компактним табличним способом задання логічних функцій є використання двовходових таблиць істинності. Для побудови такої таблиці змінні, від яких залежить логічна функція, поділяють на дві групи. У випадку парної кількості змінних ці групи рівні по кількості змінних, а у випадку не парної кількості – групи відрізняються на одну змінну. Для утворення груп змінних визначають усі набори їх значень. Рядки таблиці довільно позначають наборами змінних першої групи, а стовпці таблиці - наборами змінних другої групи. Кожна клітина такої таблиці відповідає одному набору значень змінних, від яких залежить функція. У кожній клітині таблиці проставляють значення функції на відповідному їй наборі значень змінних. Кількість клітин такої таблиці відповідає кількості усіх наборів значень змінних. Прикладом двовходових таблиць є табл. 5,6. В табл. 5 наведено приклад задання функції від трьох, а в табл. 6 – функцію від чотирьох змінних.

Булеві функції, які залежать від великої кількості змінних, задавати таблицею істинності незручно в силу її громіздкості. Наприклад, таблиця істинності для булевої від 8 змінних буде містити 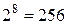рядків. Тому для задання функцій від багатьох змінних більш зручно користуватися аналітичним способом.

При аналітичному способі булева функція задається формулами, тобто аналітичними виразами, побудованими на основі операцій булевої алгебри. Аналітичний спосіб задання булевих функцій займає особливе місце в проектуванні цифрових пристроїв, оскільки усі перетворення булевих функцій, які необхідні для побудови цифрових схем, виконуються саме в аналітичному вигляді.