Теорема о движении центра масс механической системы

Составить все 3·n дифференциальных уравнений движения n точек механической системы довольно сложно. Поэтому для изучения движения механической системы чаще применяют следующую теорему: движение всей механической системы можно рассматривать как движение одной точки - центра масс.

Доказательство. Представим формулу (3.2) в следующем виде:

.

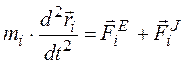Сложим правые части выражений (3.3) для каждой точки и приравняем ее к сумме левых частей данных выражений:

;

.

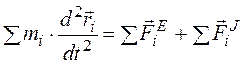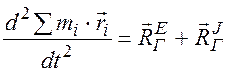Причем 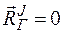. Из выражения (3.1) следует, что

.

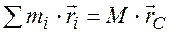С учетом этого формула (3.4) примет вид

.

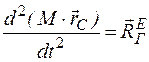Или

.

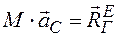Проецируем последнее выражение на оси координат:

.

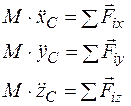
Теорема о движении центра масс звучит следующим образом: центр масс механической системы движется как материальная точка с массой равной массе всей системы, к которой приложены все внешние силы, действующие на систему.

Используя вышеописанные уравнения можно определять движение центра масс системы, не определяя движения отдельных ее точек.

Если в качестве механической системы рассматривать твердое тело, то полученные выражения будут являться дифференциальными уравнениями поступательного движенияданного тела. Поэтому поступательно движущееся тело можно рассматривать как материальную точку с массой, равной массе всего тела.

Следствия из теоремы:

1) Внутренние силы не влияют на движения центра масс системы. Т.е. внутренними силами без внешних, нельзя вывести из равновесия или изменить движение центра масс системы.

Два других следствия из рассматриваемой теоремы выражают закон сохранения движения центра масс системы.

2) если на механическую систему не действуют внешние силы или их геометрическая сумма равна нулю ( 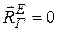), то такая система движется прямолинейно и равномерно ( ).

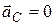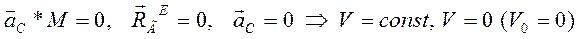
3) то же самое справедливо, если рассматривать движение механической системы относительно любой оси.

Если внешние силы действующие на механическую систему таковы, что сумма их проекций на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная.

( ).

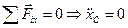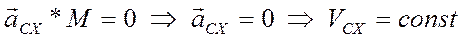
Следствия из теоремы подтверждаются следующими примерами:

Центр масс искусственного спутника земли не меняет характер своего движения при выходе космонавта в открытый космос.

2. При отсутствии трения человек не может перемещаться по совершенно гладкой поверхности.

3. Силы, действующие на колеса автомобиля со стороны двигателя, не могут привести его в движение. Движение осуществляется только при появлении внешних сил - сил сцепления (Fсц).

Решение задач

Условие задачи. Человек весом G₁ стоит на корме лодки весом G₂ и длинной l, находящейся в покое в стоячей воде. Определить, пренебрегая сопротивлением воды, расстояние S, на которое переместится лодка, если человек перейдет на нос лодки.

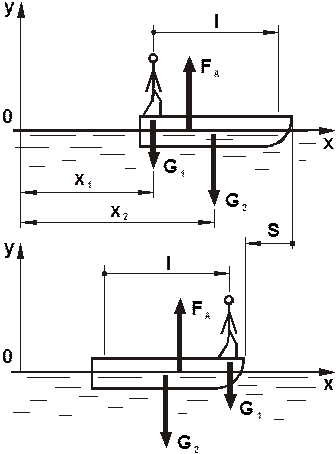
Решение. Рассмотрим механическую систему, состоящую из человека и лодки, на которую действуют: силы тяжести G₁, G₂ и сила Архимеда F_А, выталкивающая лодку из воды.

На основании теоремы о движении центра масс имеем:

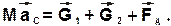
Так как все силы вертикальны, то в проекции на ось x записанное выражение примет вид

Дважды интегрируя полученное дифференциальное уравнение будем иметь:

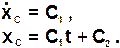
При условии, что в начальный момент времени (t=0) скорость центра масс системы равна нулю ( 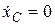), а координата x_С центра масс определяется некоторой величиной A (x_C=A), получаем: C₁=0, C₂=A, и, следовательно,

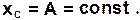
Иными словами, в процессе движения человека по лодке, координата x_C своего значения менять не будет, и перемещение человека будет компенсироваться обратным перемещением лодки.

Выражения, определяющие координату x_C центра масс системы до и после перемещений человека и лодки, соответственно, будут иметь вид:

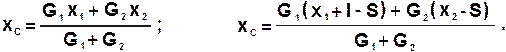
Приравняв правые части последних выражений, получим:

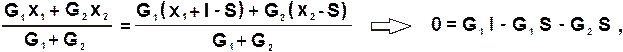
откуда

.
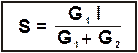