Смешанное соединение резисторов

Смешанное соединение резисторов. Смешанным соединением резисторов называется такоесоединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.

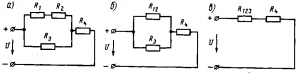Рис. 27. Схемы смешанного соединения сопротивлений

Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R₁₂₃=R₁₂R₃/(R₁₂+R₃)=(R₁+R₂)R₃/(R₁+R₂+R₃).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R_эк = R₁₂₃ + R₄ = (R₁ + R₂) R₃ / (R₁ + R₂ + R₃) + R₄

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

Метод свертывания схем (метод эквивалентных преобразований) может быть применен, если в цепи имеется только один источник электрической энергии. Метод заключается в последовательном упрощении схемы путем замены параллельных, последовательных и других («звезда», «треугольник», «многоугольник») соединений сопротивлений эквивалентными сопротивлениями. В конечном виде схема представляет собой контур, состоящий только из источника и эквивалентного сопротивления. По этой схеме находится входной ток. Для нахождения остальных токов и напряжений преобразования ведут в обратном порядке, разворачивая схему. При анализе электрических цепей используются законы Ома и Кирхгофа.

В соответствии с методом свертывания, отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению, включенному к зажимам источника. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним, эквивалентным по сопротивлению. Определяют ток в упрощенной схеме, затем возвращаются к исходной схеме и определяют в ней токи.
Рассмотрим схему на рис. 3.1. Пусть известны величины сопротивлений R1, R2, R3, R4, R5, R6, ЭДС Е. Необходимо определить токи в ветвях схемы. . Метод активных и реактивных составляющих токовЭлектротехника курсовая работа

Узел – это участок электрической цепи, содержащий соединения трех или более числа ветвей. В узловой точке происходит разветвление токов.

Узел цепи в электронике — точка, в которой соединяются три (или более) проводника электрической цепи. Узел (наряду с контуром) является базовым понятием, необходимым при анализе электрических цепей. Единственной характеристикой узла является его потенциал. Понятие узла применимо только для цепи из «одномерных» элементов, то есть таких, что их толщина бесконечно мала и ею можно пренебречь^[1].

Узел может быть сколь угодно протяжённым, поскольку для проводника с достаточно низким сопротивлением потенциал практически одинаков во всех точках проводника. Например, вся земляная шина в электронной схеме — это один узел с нулевым потенциалом.

Ничто не запрещает также считать узлом точку соединения двух проводников, однако под такое определение подпадает вообще любая точка цепи.

Ветвь – это участок электрической цепи от одного узла до другого узла. Ветвь обычно содержит один или несколько последовательно соединенных элементов цепи: сопротивления, источники ЭДС или источники тока.

Ветвь - это участок электрической цепи (схемы), по которому течет один и тот же ток. На электрических схемах ветвью называется участок между двух узлов.

Контур - это замкнутый участок электрической цепи (схемы), составленный из одной или нескольких ветвей. Любой замкнутый путь, проложенный через ветви цепи и есть замкнутый контур.

ПЕРВЫЙ ЗАКОН КИРХГОФА

Законы Кирхгофа (более корректно - правила Киргхгофа) применяются при расчете сложных (разветвленных) электрических цепей. Предлагаю рассмотреть их по очереди и начать, естественно, с первого.

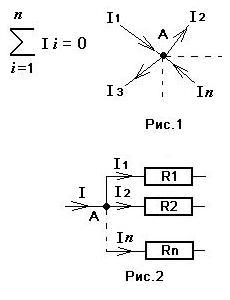Определение и формула первого закона Кирхгофа, который гласит: алгебраическая сумма токов, сходящихся в узле равна нулю, иллюстрируются рисунком 1.

Здесь:

• I i - ток в узле,
• n - число проводников, сходящихся в узле,
• токи, втекающие в узел (I₁, In) считаются положительными,
• вытекающие токи (I₂, I₃) - отрицательными.

В таком виде этот закон звучит и выглядит, наверное, очень академично, поэтому предлагаю все несколько упростить.

ВТОРОЙ ЗАКОН КИРХГОФА

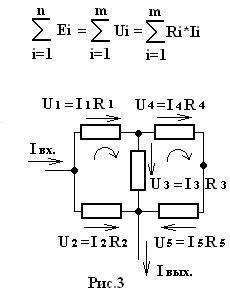Второй закон Кирхгофа определяет зависимость между падениями напряжений и ЭДС в замкнутых контурах и имеет следующий вид (рис.3) и определение:

алгебраическая сумма (с учетом знака) падений напряжений на всех ветвях любого замкнутого контура цепи, равна алгебраической сумме ЭДС ветвей этого контура.

При отсутствии в контуре ЭДС сумма падений напряжений равна 0.

Теперь несколько пояснений по практическому применению этого правила Кирхгофа:

• поскольку, алгебраическая сумма требует учета знака следует выбрать направление обхода контура ( на рис.3 - по часовой стреклке), токи и напряжения, совпадающие с этим направлением считать положительными, иные - отрицательными. При затруднении в определении направления тока, возьмите произвольное, если в результате вычислений получите результат со знаком "-", поменяйте выбранное направление на противоположенное.
• для нашего примера можно записать:
  U₁+U₃-U₂=0
  U₄+U₅-U₃=0
• кроме того, руководствуясь первым правилом Кирхгофа :
  I_вх - I₁ - I₂ = 0
  I₁ - I₃ - I₄=0
  I₄ - I₅=0
  I₂ + I₃ + I₅ - I_вых=0,

получаем систему из 6 уравнений, полностью описывающую рассматриваемую электрическую цепь.

В методе контурных токов за основные неизвестные величины принимают контурные токи, которые замыкаются только по независимым контурам (главным контурам). Контурные токи находят, решая систему уравнений, составленную по второму закону Кирхгофа для каждого контура. По найденным контурным токам определяют токи ветвей схемы.

Алгоритмом метода контурных токов:

1. Задаются направлением токов ветвей и обозначают их на схеме.

2. Определяют независимые контуры и их нумеруют. При наличии в схеме источников токанезависимые контуры, для которых составляются уравнения метода контурных токов, можно определить, если мысленно удалить источники тока.

3. Выбирают направление контурных токов (целесообразно в одну сторону) и составляют уравнения по методу контурных токов, обходя каждый контур в направлении его контурного тока. Контурный ток, проходящий через источник тока, известен и равен току источника тока (через источник тока проходит только один контурный ток!).

4. Полученную систему алгебраических уравнений решают относительно неизвестных контурных токов.

5. Искомые токи по методу контурных токов находят как алгебраическую сумму контурных токов, проходящих по данной ветви. Токи в ветвях связи равны контурным токам.

Решение задач методом контурных токов

Задача 1.3.1. Определить токи в ветвях схемы рис. 1.3.1 методом контурных токов. Правильность решения проверить по балансу мощностей.

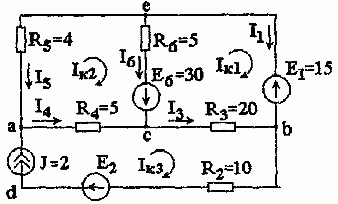
Рис. 1.3.1

Решение

1. В соответствии с алгоритмом, зададимся направлением токов ветвей и обозначим их на схеме рис. 1.3.1.

2. Определяем независимые контура и выбираем направления контурных токов I_к1, I_к2, I_к3.

3. Поскольку в схеме имеется ветвь, содержащая источник тока J, контурный ток I_к3 = J, а для контурных токов I_к1 и I_к2 запишем систему уравнений метода контурных токов:

{Iк1⋅(R3+R6)−Iк2⋅R6−J⋅R3=−E1−E6Iк2⋅(R4+R5+R6)−Iк1⋅R6−J⋅R4=E6{Iк1⋅(R3+R6)−Iк2⋅R6−J⋅R3=−E1−E6Iк2⋅(R4+R5+R6)−Iк1⋅R6−J⋅R4=E6

или

{    Iк1⋅(R3+R6)−Iк2⋅R6                             =−E1−E6+J⋅R3−Iк1⋅R6                 +Iк2⋅(R4+R5+R6)=E6+J⋅R4{    Iк1⋅(R3+R6)−Iк2⋅R6                             =−E1−E6+J⋅R3−Iк1⋅R6                 +Iк2⋅(R4+R5+R6)=E6+J⋅R4

Подставив значения сопротивлений, получаем численную систему уравнений метода контурных токов с двумя неизвестными контурными токами:

{    25Iк1     −5Iк2=−5   −5Iк1+14Iк2=40{    25Iк1     −5Iк2=−5   −5Iк1+14Iк2=40

откуда

Iк1=0,4  A;   Iк2=3  A.Iк1=0,4  A;   Iк2=3  A.

4. Определяем токи в ветвях схемы по методу контурных токов:

I1=Iк1=0,4  A;   I5=−Iк2=−3  A;   I6=Iк2−Iк1=3−0,4=2,6  A.I1=Iк1=0,4  A;   I5=−Iк2=−3  A;   I6=Iк2−Iк1=3−0,4=2,6  A.

Хотя все токи в ветвях можно определить методом контурных токов (I₃ = I_к3 – I_к1; I₄ = I_к3 – I_к2), токи I₃ и I₄ определим по первому закону Кирхгофа. Составим уравнения по первому закону Кирхгофа:

для узла a:

−I5−J+I4=0,−I5−J+I4=0,

откуда

I4=I5+J=(−3)+2=−1  A;I4=I5+J=(−3)+2=−1  A;

для узла b:

−I1−I3+J=0,−I1−I3+J=0,

откуда

I3=J−I1=2−0,4=1,6  A.I3=J−I1=2−0,4=1,6  A.

5. Правильность решения проверяем по балансу мощностей. Предварительно находим напряжение на зажимах источника тока:

Uad=φa−φd=J⋅R2+I3⋅R3+I4⋅R4−E2=         =2⋅10+1,6⋅20+(−1)⋅5−10=37  B.Uad=φa−φd=J⋅R2+I3⋅R3+I4⋅R4−E2=         =2⋅10+1,6⋅20+(−1)⋅5−10=37  B.

Тогда

   E2⋅J+Uad⋅J+E1⋅(−I1)+E6⋅I6=J2⋅R2+I23⋅R3+I24⋅R4+I25⋅R5+I26⋅R6;10⋅2+37⋅2+15⋅(−0,4)+30⋅2,6=22⋅10+1,62⋅20+(−1)2⋅5+(−3)2⋅4+2,62⋅5;                                                                  166  Вт=166  Вт.   E2⋅J+Uad⋅J+E1⋅(−I1)+E6⋅I6=J2⋅R2+I32⋅R3+I42⋅R4+I52⋅R5+I62⋅R6;10⋅2+37⋅2+15⋅(−0,4)+30⋅2,6=22⋅10+1,62⋅20+(−1)2⋅5+(−3)2⋅4+2,62⋅5;                                                                  166  Вт=166  Вт.

Метод узловых напряжений состоит в определении напряжений между узлами сложной электрической цепи путем решения уравнений, составленных по первому закону Кирхгофа, куда в качестве неизвестных входят напряжения между узлами цепи. Этот метод позволяет уменьшить количество уравнений системы до величины: (k-1), где k - количество узлов сложной электрической цепи. Данный метод целесообразно использовать, когда l>2(k - 1), где l - количество ветвей сложной электрической цепи.

Узловыми напряжениями называют напряжения между каждым из (k-1) узлов и одним произвольно выбранным опорным узлом. Потенциал опорного узла принимается равным нулю. На схеме такой узел обычно отображают как заземленный.

Сущность метода заключается в том, что вначале решением системы уравнений определяют потенциалы всех узлов схемы по отношению к опорному узлу. Далее находят токи всех ветвей схемы с помощью закона Ома по формуле (1.16).

Расчет сложных электрических цепей методом узловых напряжений производят в следующей последовательности:

1. Вычерчиваем принципиальную схему и все ее элементы.
2. На схеме произвольно выбирают и обозначают опорный узел. В качестве опорного желательно выбирать узел, в котором сходится максимальное количество ветвей.
3. Произвольно задаемся направлением токов всех ветвей и обозначаем их на схеме.
4. Для определения потенциалов остальных (k-1) узлов по отношению к опорному узлу составляем следующую систему уравнений:
5. Решаем любым методом полученную систему относительно узловых напряжений и определяем их.
6. Далее для каждой ветви в отдельности применяем закон Ома (1.16) и находим все токи в электрической цепи.
   

Расчет сложной электрической цепи по данной методике приведен в примере №14.

Рассмотрим применение метода узловых напряжений для расчета электрических цепей более подробно на примере схемы, взятой из предыдущего раздела.

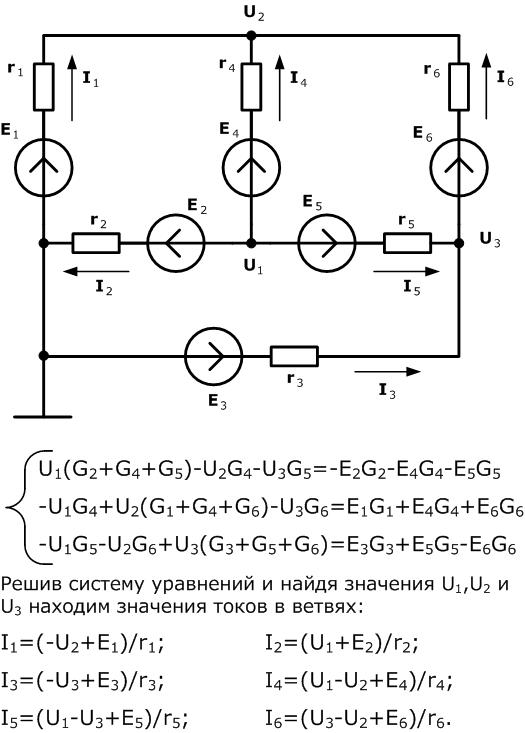
Более предметно расчет данной цепи методом узловых напряжений изложен в примере №15.