Классификация видов и методов моделирования систем

2.5.1. Классификационные признаки

Классификация видов моделирования представлена ниже.

Первый признак классификации видов моделирования – это степень полноты модели. Условная схема такой классификации приведена на рисунке 2.1.

Особенности того или иного вида моделирования наглядно демонстрируется таблицей 2.1.

Таблица 2.1. Виды моделирования и их особенности

Виды моделирования	Отличительные особенности вида моделирования
Детерминированное	Отображает процессы, в которых отсутствуют случайные воздействия
Стохастическое	Отображает вероятностные (стохастические) процессы и события
Статическое	Служит для описания поведения объекта в какой-либо момент времени
Динамическое	Отображает поведение объекта во времени
Дискретное	Для описания процессов, которые предполагаются дискретными
Непрерывное	Отражает непрерывные процессы
Дискретно-непрерывное	Отражает как дискретные, так и непрерывные процессы
Мысленное	Часто является единственным способом моделирования объектов, которые либо практически нереализуемы в заданном интервале времени, либо существуют вне условий, возможных для их физического создания
Наглядное	Отображает явления и процессы, протекающие в объекте
Гипотетическое	Закладывается гипотеза о закономерностях протекания процесса в реальных объектах
Аналоговое	Применяются аналоги различных уровней
Макетирование	Применяется в случаях, когда протекающие в реальных объектах процессы не поддаются физическому моделированию, либо могут предшествовать проведению других видов моделирования
Знаковое	Отображение понятий с помощью знаков, описание какого-то реального объекта в отдельных символах
Языковое	В основе лежит некоторый тезаурус – словарь, который очищен о неоднозначности, т.е. в нем каждому слову может соответствовать лишь единственное понятие
Символическое	Искусственный процесс создания логического объекта

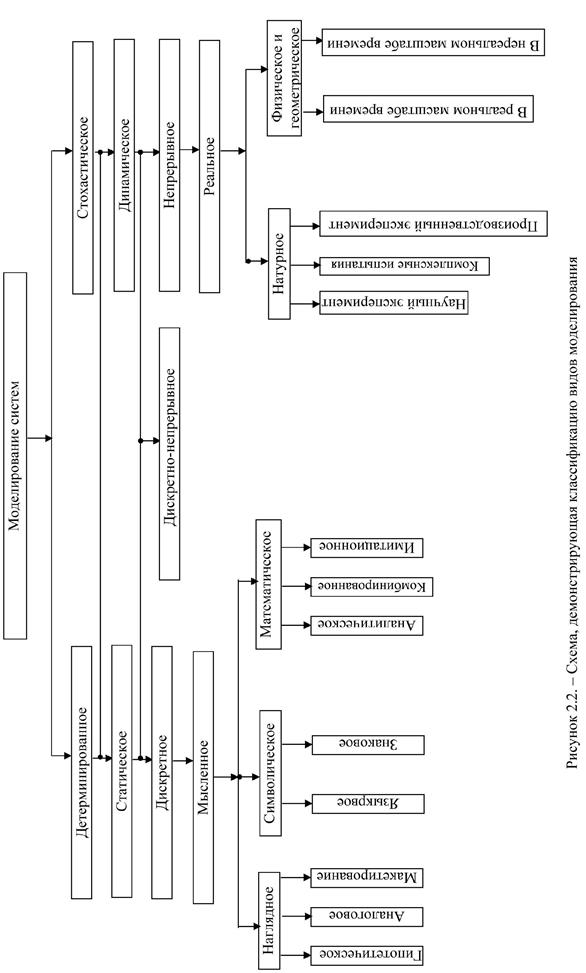
Наиболее общая схема классификации видов моделирования представлена на рисунке 2.2.

Применение того или иного вида и/или метода моделирования определяется в каждом конкретном случае в зависимости от исследуемой системы.

Дадим характеристики отдельных основных видов и методов моделирования подробнее.

2.5.2. Математическое моделирование.

Для исследования характеристик процесса функционирования любой системы S математическими методами должна быть проведена формализация этого процесса, т.е. построена математическая модель.

Под математической моделью понимается процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющей получить характеристики реального объекта.

Отличают математические модели аналитические, имитационные и комбинированные.

Аналитические модели – это процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегро-дифференциальных, конечно-разностных и др.) или логических соотношений.

Аналитическая модель может быть исследована следующими методами:

- аналитическим, при котором в общем виде получают явные зависимости для исследования характеристик);

- численным, при котором не умея решать уравнений в общем виде, стремятся получить числовые результаты при конкретных начальных данных;

- качественным, при котором не имея значения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).

Имитационное моделирование – наиболее эффективный метод исследования больших систем.

При таком моделировании алгоритм воспроизводит процесс функционирования системы S во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени.

В процессе имитационного моделирования происходит воспроизведение процессов, объектов или явлений с имитацией случайными величинами и случайными процессами динамических свойств звеньев оригиналов, которые не удается представить определенными математическими зависимостями.

Метод статистического моделирования – метод машиной реализации имитационной модели, а метод статистических испытаний (метод Монте-Карло) – это численный метод решения аналитической задачи.

Комбинированное моделирование объединяет достоинства аналитического и имитационного моделирования.

В целом можно сказать, что при математическом моделировании в качестве объекта оригинала выступают исходные уравнения, представляющие математическую модель объекта. А в качестве модели – сами процессы, протекающие в соответствии с этими уравнениями, которые воспроизводятся или аналитически, или на ЭВМ (ЦВМ) в виде машинных решений.

При математическом моделировании наряду с ЭВМ также достаточно широко используются аналоговые вычислительные машины (АВМ) как консольные или терминальные устройства на рабочих местах разработчиков и испытателей.

Реальное моделирование

Реальное моделирование –это исследование различных характеристик системы либо на реальном объекте целиком, либо на его части.

Натурное моделирование

Это проведение исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия.

Производственный эксперимент и комплексные испытания

Они обладают высокой степенью достоверности.

Научный эксперимент

Научный эксперимент характеризуется широким использованием средств автоматизации проведения, применения разнообразных средств обработки информации, возможностью вмешательства человека в процесс эксперимента.

Физическое и геометрическое моделирование

Оно отличается от натурного тем, что исследование проводится на установках, которые сохраняют природу явлений и обладают физическим и геометрическим подобием.

При физическом и геометрическом моделировании необходимо иметь набор правил и условий, выполнение которых обеспечивает требуемую точность изучения заданного объекта по его модели.

В частности, это требование условий обеспечения подобия объекта–модели и объекта-оригинала. Объекты считаются подобными. если характеристики процесса. происходящие в какой-либо из них отличаются от соответствующих характеристик другого объекта вполне определенными и постоянными для данного процесса коэффициентами.

В общем случае модель изучаемого объекта может быть иной физической природы, отличной от природы оригинала.

Полунатурное моделирование

Особое место в моделировании систем занимает полунатурное моделирование. Оно отличается тем, что при нем в систему подключается реальная аппаратура, элементы которой необходимо исследовать совместно с моделью остальной части системы, реализованной на ЭВМ.

(Например, контур слежения в системах теленаведения с подключением реального пульта управления в виде джойстика).

При полунатурном моделировании систем управляемых объектов возникает необходимость моделирования в реальном масштабе времени.

Целью при этом является определение влияния кинематики и динамики устройств САУ на работу САУ в целом. При этом ряд элементов этой САУ не поддаются математическому описанию и аппаратурной реализации.

Построение модели

Модель выражает взаимосвязь между управляемым переменными, неуправляемыми переменными, технологическими параметрами и показателем эффективности.

Существует несколько различных типов соотношений, формирующих модель.

1) Соотношения, вытекающие из различных фундаментальных законов природы, вариационных принципов, аналогий, иерархических цепочек.

Например, это закон сохранения энергии, материи, импульса.

2) Эмпирические соотношения. Они также характеризуют взаимосвязь между характеристиками системы и свойствами элементов.

Эмпирические соотношения выводятся на основе изучения данных за прошлый период, из анализа технических аспектов.

Получение эмпирических соотношений затрудняется следующими двумя причинами:

Во-первых, имеющиеся данные ретроспективного анализа могут оказаться не представительными для вывода соотношений, характеризующих рассматриваемую систему в изменяющихся условиях.

Эти новые условия функционирования системы должны найти отражение в изменении числовых значений, соответствующих параметров, входящих в рассматриваемые соотношения, либо в изменении структуры или характера самих уравнений.

Во-вторых, эмпирические соотношения могут выводиться на основе данных, которые относятся к характеристикам функционирования системы, не отвечающему требуемому уровню эффективности.

3) При формировании моделей также используются нормативныесоотношения. Это такие соотношения, которые устанавливают, какпеременные, характеристики, параметры объекта должны быть связаны между собой в будущем, а не те, которые описывают связи в уже существующих или в существовавших аналогах.