Предельный коэффициент усиления

Построение годографа Михайлова осуществляется по виду левой части характеристического уравнения замкнутой системы, величина свободного коэффициента 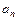которого определяет начальную точку годографа при значении 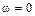. В этот свободный коэффициент всегда входит коэффициент усиления системы K.

При увеличении значения K соответствующим образом увеличивается абсцисса каждой точки годографа Михайлова, и вся кривая смещается вправо. При некотором значении K годограф может переместиться настолько, что пройдет через начало координат, и условие устойчивости системы будет нарушено.

Значение коэффициента усиления системы, при котором она находится на границе устойчивости, называют предельным (критическим) коэффициентом усиления 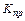. При уменьшении коэффициента усиления неустойчивой системы до величины, меньшей предельного значения, система становится устойчивой.

Пример 12. Используя частотные критерии устойчивости, определить предельный коэффициент усиления системы, структурная схема которой представлена на рисунке 2.4.

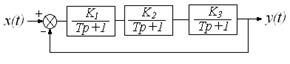
Рисунок 2.4 – Структурная схема системы

а) По критерию Найквиста необходимо рассчитать амплитудную и фазовую частотные характеристики разомкнутой системы:

,

,

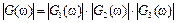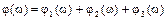где 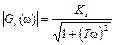– АЧХ инерционного звена 1-го порядка;

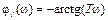– ФЧХ инерционного звена 1-го порядка;

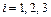– номер звена в системе.

Таким образом, для разомкнутой системы получим

,

,

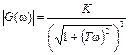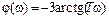где 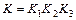– общий коэффициент усиления системы.

Нахождение системы на границе устойчивости соответствует прохождению годографа Найквиста через точку с координатами 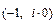. Это означает, что при граничной частоте, на которой абсолютное значение фазы разомкнутой системы равно 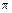, амплитудная частотная характеристика разомкнутой системы должна быть равна единице:

, откуда .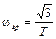

В результате получим

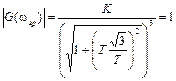, откуда .

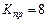б) По критерию Михайлова необходимо получить характеристическое уравнение замкнутой системы. Для этого сначала рассчитаем ее передаточную функцию:

.

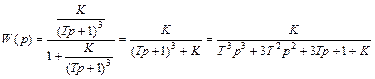Характеристическое уравнение примет вид

.

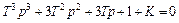Далее осуществим переход к частотной переменной, используя замену :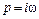

.

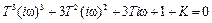Выделим в левой части получившегося уравнения действительную и мнимую части:

,

.

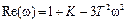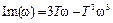Далее найдем их положительные корни:

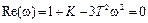, откуда .

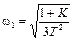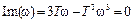, откуда , .

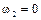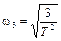По критерию Михайлова для устойчивости системы необходимо, чтобы корни функций Re(w) и Im(w) чередовались с ростом частоты, начиная с 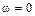, то есть должны выполняться неравенства

.

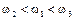Поскольку 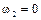, неравенство 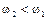будет выполнено для любого положительного значения 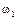, поэтому для устойчивости системы необходимо, чтобы 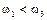. Очевидно, что режим границы устойчивости будет соответствовать равенству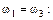

,

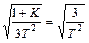откуда 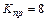.