Передаточные функции разомкнутых и замкнутых САУ

При анализе САУ в результате структурных преобразований, чаще всего стремятся получить одноконтурную САУ, так как методы анализа и синтеза подобных систем разработаны наиболее полно. Рассмотрим простейшую одноконтурную САР (рисунок 4.6, а). Она представляет собой систему с главной отрицательной обратной связью. Произведем размыкание системы в точке «А».

Передаточной функцией разомкнутой системы W_p(p) называется отношение изображения по Лапласу сигнала обратной связи к изображению по Лапласу сигнала ошибки при нулевых начальных условиях, т.е.

(4.14)

Следует иметь в виду, что для разомкнутой системы X(t)=DX(t) и все возмущающие воздействия считаются равными нулю.

Таким образом, передаточная функция разомкнутой системы равна произведению передаточных функций отдельных звеньев разомкнутого контура, включая передаточную функцию элемента обратной связи.

Рисунок 4.6 Преобразования одноконтурной САУ

При анализе САУ, особенно следящих, возникает необходимость анализа поведения ошибки управления. Для этого составляют передаточную функцию относительно ошибки управления.

Передаточной функцией замкнутой системы по ошибке регулирования называется отношение изображения по Лапласу ошибки регулирования к изображению по Лапласу управляющего воздействия. Ошибка регулирования в САР выявляется после узла сравнения. Если выходной величиной САР считать ошибку регулирования DX(t), а входной - управляющее воздействие X(t), то структурная схема примет вид, показанный на рисунке 4.6, б.

Пользуясь правилами преобразования, получим передаточную функцию для ошибки воспроизведения управляющего воздействия.

, (4.15)

Аналогично можно написать передаточную функцию и для любой координаты САР, например Y₂(t).

Из структурной схемы (рисунок 4.6, в), считая Y₂(t) выходной величиной, получим

, (4.16)

Рассмотрим случай, когда к САУ приложено несколько возмущающих воздействий (рисунок 4.7, а). Как было показано ранее, каждому возмущающему воздействию соответствует передаточная функция, причем все остальные возмущения и управляющие воздействия полагаются равными нулю. Составим передаточную функцию относительно возмущения f₁(t) (рисунок 4.7, б). Из структурной схемы следует

, (4.17)

Из выражения (4.17) следует, что передаточная функция замкнутой САУ по данному возмущению равна дроби, в числителе которой передаточная функция прямого канала от точки приложения возмущения до выходной величины, а в знаменателе - единица плюс передаточная функция разомкнутой системы.

Согласно принципу суперпозиции, реакция выходной величины определяется как сумма реакций от каждого из воздействий, т.е.

Рисунок 4.7 Одноконтурная САУ при приложении нескольких воздействий

, (4.18)

где

;

;

W₁(p),W₂(p),W₃(p) - передаточные функции прямых цепей элементов, заключенных между точками приложения воздействий и выходной величиной.

Известно, что при исследовании свободного движения САУ оперируют характеристическим уравнением системы. Найдем характеристические полиномы разомкнутой и замкнутой САУ.

Для разомкнутой системы можно записать уравнение:

, (4.19)

где D_p(p) - характеристичекий полином разомкнутой системы.

Для замкнутой системы получим:

, (4.20)

Пусть 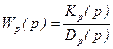, тогда характеристическое уравнение замкнутой системы

, (4.21)

или

, (4.22)

Таким образом, характеристическое уравнение замкнутой САУ при отрицательной обратной связи равно сумме характеристических полиномов левой и правой части уравнения разомкнутой системы.

Рассмотрим пример преобразований САУ к виду, удобному для анализа.

Система управления имеет два внутренних контура и один внешний. Внешний контур регулирования содержит обратную связь по скорости двигателя. Эта связь называется главной обратной связью, и поэтому система называется системой автоматического регулирования скорости. Соответственно, устройство, обеспечивающее поддержание заданного алгоритма функционирования, называется регулятором скорости.

Внутренние контуры регулирования являются вспомогательными и предназначены для улучшения характеристики объекта управления и поддержания промежуточных координат САР в заданных пределах с целью компенсации вредного влияния внутренних возмущений и инерционностей системы.

В данном случае имеем два внутренних контура - контур напряжения и контур тока. Подробно принципы построения таких систем будут рассмотрены в курсе «Автоматическое управления электроприводами», поэтому мы остановимся лишь на вопросах, связанных с преобразованием таких структурных схем. Рассмотрим каждый контур в отдельности.

Контур напряжения включает в себя: регулятор напряжения (РН), тиристорный возбудитель, генератор с передаточными функциями:

; (4.23)

; (4.24)

. (4.25)

При анализе такие системы, как правило, приводят к единичной обратной связи так, как это показано на рисунке 4.8, а.

Рисунок 4.8 Структурные схемы контура напряжения

Учитывая (4.23) и правило последовательного соединения звеньев, структурная схема (рисунок 4.8, б) может быть представлена одним эквивалентным звеном с передаточной функцией

, (4.26)

Управляющим воздействием для контура тока является сигнал задания тока двигателя U_зт, а выходной величиной ток двигателя. Регулятор тока имеет передаточную функцию

, (4.27)

С учетом (4.26), (4.27) структурная схема контура тока приведенного к единичной обратной связи представлена на (рисунке 4.9, а).

Такая структурная схема получена при условии, что Т_м>>Т_э. В этом случае пренебрегают обратной связью по ЭДС двигателя т.е. полагают, что E=K_E×w=0. В результате W_к(p)=1. После преобразования структурная схема замкнутого контура тока примет вид, показанный на (рисунок 4.9, б).

Этой структурной схеме может быть поставлена в соответствие передаточная функция замкнутого контура тока

, (4.28)

Учитывая, что замкнутый контур тока является внутренним по отношению к контуру скорости, и приводя к единичной обратной связи, получим структурную схему, изображенную на (рисунок 4.9, в). В данном случае считаем, что передаточная функция регулятора известна и имеет вид

, (4.29)

Из структурной схемы видно, что к системе прикладывается два воздействия - управляющее U_вх(t) и возмущающее I_с(t). Полагая U_вх(t)=0, I_с(t)=0 и размыкая обратную связь, получим передаточную функцию разомкнутой системы (рисунок 4.9, г)

, (4.30)

Передаточная функция по управляющему воздействию

, (4.31)

Принимая за входную величину возмущающее воздействие, получим структурную схему, представленную на (рисунке 4.9, в).

Этой структурной схеме соответствует передаточная функция по возмущающему воздействию

, (4.32)

Таким образом, мы получим структурные схемы и передаточные функции (4.31), (4.32), составленные относительно управляющего и возмущающего воздействий.

Используя принцип суперпозиции, мы можем записать выражение для определения реакции системы при одновременном приложении возмущающего и управляющего воздействий.

, (4.33)

Рисунок 4.9 Структурные преобразования САУ

Таким образом:

1) Применение аппарата структурных преобразований позволяет значительно упростить методики исследования САУ. При этом необходимо иметь в виду, что упрощение структурных схем ведет к повышению порядка дифференциального уравнения, описывающего поведение координат САУ;

2) Применение принципа суперпозиций позволяет определить реакцию системы при одновременном приложении нескольких возмущающих и управляющих воздействий. Исследования САУ могут проводиться отдельно для любого из воздействий. В этом случае принимают, что остальные воздействия равны нулю;

3) При исследовании многоконтурных САУ, имеющих внутренние автономные контуры, каждый контур исследуется отдельно, начиная с внутреннего;

4) В большинстве случаев при исследовании САУ последние приводятся к простейшим одноконтурным системам с единичной обратной связью.