Интегрирование рациональных дробей
Рациональной дробью называется дробь вида 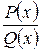 , где
, где 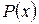 и
и 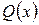 – многочлены. Рациональная дробь называется правильной, если степень числителя
– многочлены. Рациональная дробь называется правильной, если степень числителя 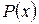 ниже степени знаменателя
ниже степени знаменателя 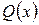 ; в противном случае дробь называется неправильной.
; в противном случае дробь называется неправильной.
Элементарными рациональными дробями называются правильные дроби вида:
1. 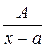 ;
;
2. 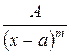 , где
, где 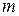 – целое число, большее единицы;
– целое число, большее единицы;
3. 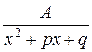 , где
, где 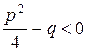 , т.е. квадратный трехчлен
, т.е. квадратный трехчлен 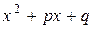 не имеет действительных корней;
не имеет действительных корней;
4. 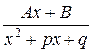 .
.
Во всех четырех случаях предполагается, что 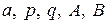 – действительные числа.
– действительные числа.
Рассмотрим интегралы от элементарных рациональных дробей первых двух типов. Имеем:
1. 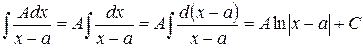 ;
;
2. 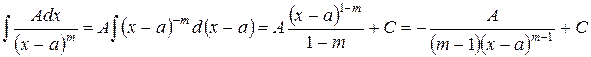 .
.
Например, 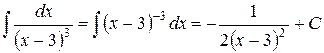 .
.
Для интегрирования дробей третьего типа выделяют полный квадрат в знаменателе, а далее используют табличные интегралы
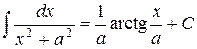 ;
; 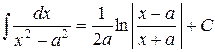 .
.
Пример. Найти интеграл 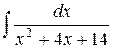 .
.
Решение. Выделим полный квадрат
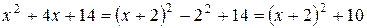 .
.
Тогда
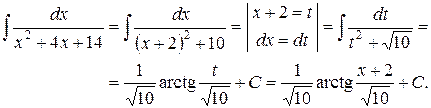
Для интегрирования элементарных дробей четвертого типа в числителе выделяют производную знаменателя и сводят интеграл к сумме двух интегралов третьего типа и 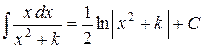 .
.
Пример. Найти интеграл 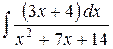 .
.
Решение. Преобразуем дробь: выделим в числителе из 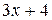 производную знаменателя, равную
производную знаменателя, равную 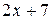 , но чтобы величина числителя не изменялась:
, но чтобы величина числителя не изменялась:
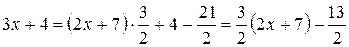 .
.
Поэтому
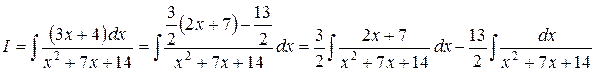 .
.
Выделим полный квадрат:
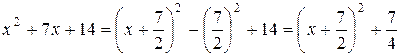 .
.
Далее имеем:
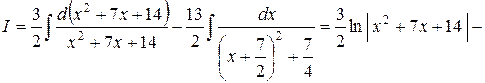
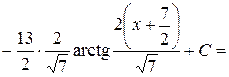
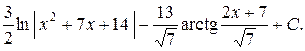
Интегрирование рациональных дробей с помощью разложения на элементарные дроби. Перед интегрированием рациональной дроби 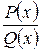 надо сделать следующие алгебраические преобразования:
надо сделать следующие алгебраические преобразования:
1) если дана неправильная рациональная дробь, то выделить из нее целую часть, т.е. представить в виде:
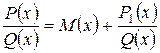 ,
,
где 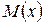 – многочлен, а
– многочлен, а 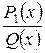 – правильная рациональная дробь;
– правильная рациональная дробь;
2) разложить знаменатель дроби на линейные и квадратные множители:
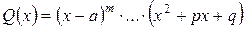 ,
,
где 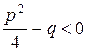 , т.е. квадратный трехчлен
, т.е. квадратный трехчлен 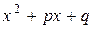 не имеет действительных корней;
не имеет действительных корней;
3) правильную рациональную дробь разложить на элементарные дроби:
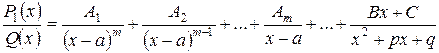
4) вычислить неопределенные коэффициенты 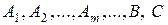 для чего привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях
для чего привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях 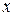 в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной
в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной 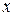 конкретные значения (корни знаменателя).
конкретные значения (корни знаменателя).
В результате интегрирование рациональной дроби сведется к нахождению интегралов от многочлена к интегралам от элементарных рациональных дробей.
Случай 1. Знаменатель имеет только действительные различные корни, т.е. разлагается на неповторяющиеся множители первой степени.
Пример. Найти интеграл 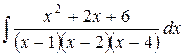 .
.
Решение. Так как каждый из двучленов 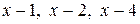 входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы элементарных дробей первого типа:
входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы элементарных дробей первого типа:
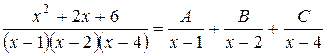 .
.
Приводя к общему знаменателю и приравнивая числители, получим
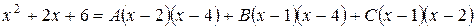 .
.
Положим
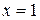 | 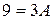 | 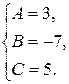 |
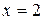 | 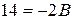 | |
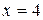 | 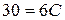 |
Итак, разложение рациональной дроби на элементарные имеет вид:
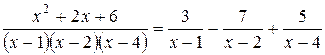 .
.
Таким образом,
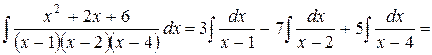
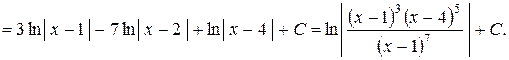
Случай 2. Знаменатель имеет лишь действительные корни, причем некоторые из них кратные, т.е. знаменатель разлагается на множители первой степени и некоторые из них повторяются.
Пример. Найти интеграл 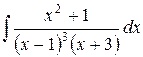 .
.
Решение. Множителю 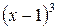 соответствует сумма трех элементарных дробей
соответствует сумма трех элементарных дробей 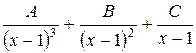 , а множителю
, а множителю 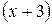 – элементарная дробь
– элементарная дробь 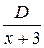 . Итак,
. Итак,
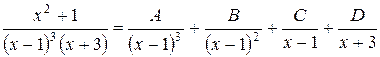 .
.
Тогда
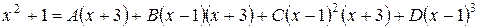 .
.
Действительными корнями знаменателя являются числа 1 и – 3. Полагая 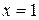 , получаем
, получаем 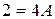 . При
. При 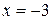 имеем
имеем 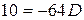 .
.
Положим 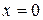 , получаем
, получаем 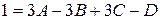 . При
. При 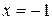 имеем
имеем 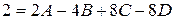 . Тогда
. Тогда
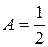 ,
, 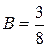 ,
, 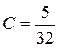 ,
, 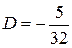 .
.
Разложение данной дроби имеет вид:
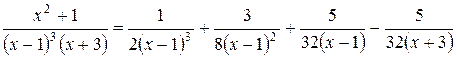 .
.
Таким образом, получим
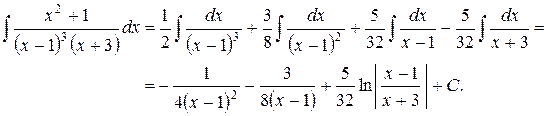
Случай 3. Среди корней знаменателя имеется квадратный трехчлен, не разложимый на линейные множители.
Пример. Найти интеграл 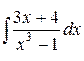 .
.
Решение.
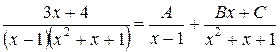 ;
;
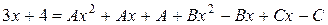 .
.
Приравняем коэффициенты при одинаковых степенях переменной 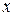 .
.
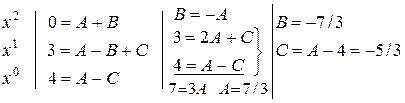 ;
;
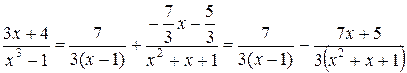 .
.
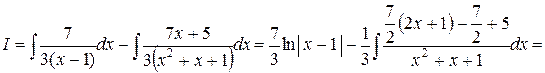
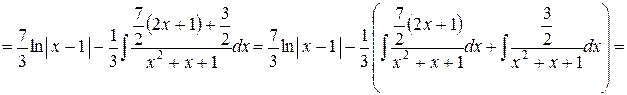
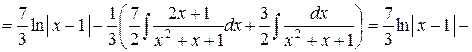
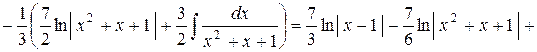
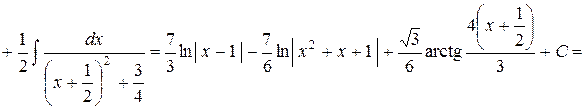
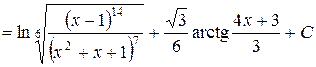 .
.
4.6. Интегрирование тригонометрических функций
1. Интегралы вида 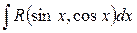 , где
, где 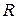 - рациональная функция.
- рациональная функция.
Интегралы указанного вида приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки: 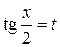 . В результате этой подстановки имеем:
. В результате этой подстановки имеем:
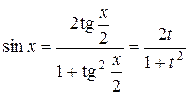
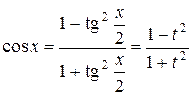
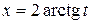
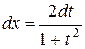 .
.
Пример. Найти интеграл 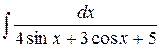 .
.
Решение. Подынтегральная функция рационально зависит от 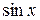 и
и 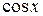 : применяем подстановку
: применяем подстановку 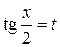 , тогда
, тогда 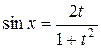 ,
, 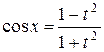 ,
, 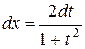 .
.
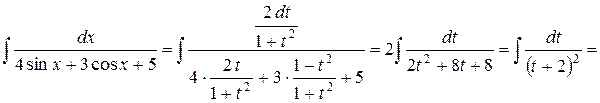
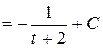 .
.
Возвращаясь к старой переменной, получаем:
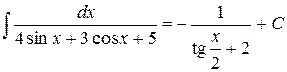 .
.
2. Интегралы вида 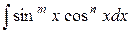 .
.
Выделим два случая, имеющие особенно важное значение.
| Случай 1. | По крайней мере один из показателей 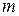 или или 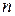 – положительное нечетное число. – положительное нечетное число. |
§ если 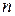 – нечетное положительное число, то применяется подстановка
– нечетное положительное число, то применяется подстановка 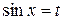 ;
;
§ если 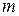 – нечетное положительное число, то применяется подстановка
– нечетное положительное число, то применяется подстановка 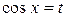 .
.
§ если 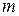 и
и 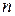 оба нечетные и
оба нечетные и 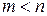 , то применяется подстановка
, то применяется подстановка 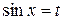 ;
;
§ если 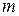 и
и 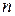 оба нечетные и
оба нечетные и 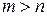 , то применяется подстановка
, то применяется подстановка 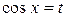 ;
;
§ если 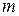 и
и 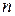 оба нечетные и
оба нечетные и 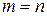 , то применяют любую из подстановок
, то применяют любую из подстановок 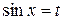 или
или 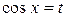 ;
;
Пример. Найти интеграл 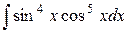 .
.
Решение. Здесь 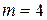 ,
, 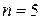 , значит применяем подстановку
, значит применяем подстановку 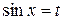 , откуда
, откуда 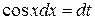 . Далее имеем:
. Далее имеем:
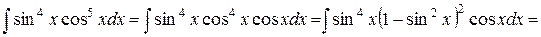
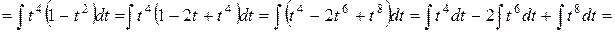
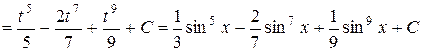 .
.
| Случай 2. | Оба показателя степени 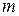 и и 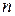 – четные положительные числа. – четные положительные числа. |
Здесь следует преобразовать подынтегральную функцию с помощью формул:
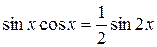
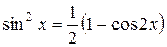
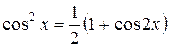
Пример. Найти интеграл 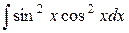 .
.
Решение. Применяем последовательно первую и вторую из этих формул:
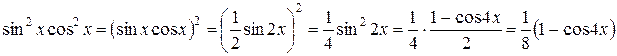 .
.
Итак,
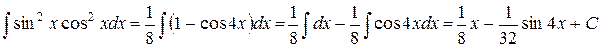 .
.
3. Интегралы вида 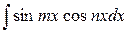 ;
; 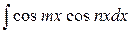 ;
; 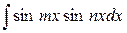 .
.
Тригонометрические формулы:
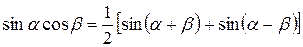
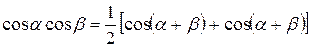
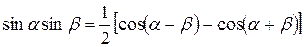
дают возможность произведение тригонометрических функций предоставить в виде суммы.
Пример. Найти интеграл 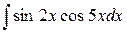 .
.
Решение. Используя первую формулу, получим
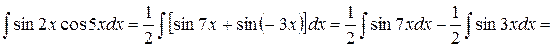
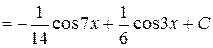 .
.
