Тема 9. Поведение индивида на рынках факторов производства.

6.

7.

8.

9.

9.1. Функция полезности потребителя: U = x∙y. Первоначально цена товара x была равна 4 ден.ед., а цена товара y: 1 ден.ед. Начальный запас составляет w_X = 4, w_Y = 8. Других источников дохода у потребителя нет. Определите:

а) оптимальный потребительский набор и тип потребителя;

б) как изменится поведение и благосостояние потребителя, если цена товара x уменьшится в 2 раза по сравнению с первоначальной;

в) оптимальный потребительский набор и тип потребителя, если цена товара x уменьшится в 4 раза по сравнению с первоначальной;

г) постройте графики валового и чистого спроса на товар x.

9.2. Нарисуйте бюджетное ограничение, если досуг R ≤ 24, а w – заработная плата за 1 час работы для ситуаций, когда:

а) других доходов нет;

б) есть доход, не зависящий от труда;

в) зарплата увеличивается при сверхурочной работе (если L > 8).

9.3. Одно из предложений[3] по поводу реформирования системы по поддержанию минимального уровня жизни в США заключается во введении отрицательного подоходного налога. При такой системе налогообложения каждый индивидуум получает денежную дотацию в размере $G в месяц. За каждый заработанный индивидуумом $1 дотация снижается на $t.

а) Пусть G = 100, t = 0.25, а ставка заработной платы w = $8 в час. Нарисуйте бюджетное ограничение до и после введения отрицательного налога. (Считайте, что в месяце 720часов).

б) Как отрицательный подоходный налог повлияет на предложение рабочей силы?

9.4. Функция полезности Виктора: U = 2C – (10 – R)², где C – объем дневного потребления продуктов питания, R – продолжительность досуга. Виктор спит 10часов в сутки и получает проценты по банковскому вкладу, равные $10 в день. Цена потребляемых благ равна $1. Сколько часов в день он будет работать, если:

а) ставка зарплаты равна w = 0;

б) ставка зарплаты равна w = $2;

в) банковские проценты увеличатся до $20 в день;

г) постройте кривую спроса на досуг и кривую предложения труда Виктора, зависит ли их форма от суммы процентов по вкладу?

9.5. Функция полезности рабочего: U = C – R² + 20R, где С – объем дневного потребления продуктов питания, R - продолжительность досуга. Рабочий спит 8часов в сутки. Нетрудовой доход равен 30ден.ед. Цена продуктов 1доллар. Определите:

а) продолжительность досуга, если за работу ему ничего не платят;

б) продолжительность досуга, если ставка зарплаты 10ден.ед. в час;

в) кривую спроса на досуг и кривую предложения труда рабочего;

г) как изменится предложение труда и благосостояние рабочего, если государство лишит его нетрудового дохода, но взамен будет выплачивать дотацию в размере 10% трудового дохода.

9.6. Функция полезности Генри3: U = CR – R² + 96R, где С – объем ежегодного потребления, R - время досуга. Генри располагает временем Т, ставка заработной платы: w. Определите функцию предложения рабочей силы Генри. Как повлияет на продолжительность его рабочего времени введение налога на заработную плату в размере 25%?

9.7. Проанализируйте общий эффект, эффекты дохода и замещения (по Хиксу) при понижении ставки заработной платы, постройте соответствующие графики. Рассмотрите следующие высказывания3:

а) «Теперь, когда тарифная ставка моей зарплаты понизилась, мне не имеет смысла работать столько часов, сколько я работал до этого».

б) «Теперь, когда тарифная ставка моей зарплаты понизилась, мне необходимо работать больше, чтобы поддерживать свой привычный уровень жизни».

9.8. Проанализируйте[4], будет ли человек работать больше, если:

а) увеличивается ставка заработной платы;

б) увеличивается оплата только сверхурочной работы.

(Покажите оба случая на одном графике.)

9.9. Жизнь Дженифер3 разделена на 2 периода. В течение первого она получает фиксированный доход в размере $10 тыс. Во втором ее доход составляет $20тыс. Нарисуйте межвременное бюджетное ограничение Дженифер, если:

а) она может брать кредиты и предоставлять ссуды по рыночной процентной ставке, равной 7%;

б) процентная ставка повысилась до 9%. Как вы думаете, каким образом это изменение отразится на размере ее сбережений?

в) Дженифер не имеет возможности брать кредит, хотя все еще может давать в долг под 9%.

9.10. Человек потребляет в двух периодах. Его функция полезности: U = lnC₁+ α∙lnC₂, где C₁, C₂ – потребление в первом и втором периоде, 0 < α < 1. Первоначальное богатство равно W, других источников дохода нет и не планируется. Разница между W и расходами в первом периоде сохраняется по ставке процента r. Определите:

а) оптимальное потребление в 1 и 2 периодах, а также тип данного потребителя;

б) как изменения в процентной ставке могут повлиять на поведение потребителя?

9.11. Функция полезности индивида в модели межвременного выбора: U = C₁∙C₂. Доход в текущем периоде составляет 200ден.ед., а в будущем планируется повышение дохода до 220ден.ед. Определите:

а) величину текущего сбережения при ставке 10%;

б) функцию предложения текущего сбережения.

9.12. Функция полезности потребителя: U =min{C₁,C₂²}. Доход потребителя в 1 периоде равен 100руб., во 2-ом – 120руб. Норма процента 25%. Цена единицы блага 1руб. Определите оптимальный уровень сбережений потребителя и предельную норму замещения между текущим (первый период) и будущим (второй период) потреблением, если:

а) инфляция отсутствует;

б) инфляция составляет 12%.

9.13. Предположим, участок земли продается по цене 60тыс. долларов. Вы оцениваете, что сможете сдавать землю в аренду, получая 5тыс. долларов в год. Земля будет приносить доход вам и вашим потомкам всегда. Купите ли вы землю при условии, что ставка ссудного процента равна 10%?

9.14. Ценность дерева непрерывно изменяется со временем по закону: 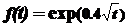. Определите:

а) оптимальный для вырубки возраст дерева, если ставка процента составляет4%;

б) как повлияет на решение о вырубке повышение ставки процента?

9.15. Предположим, что некая машина приносит доход своему владельцу в размере R = 10 тыс. долл. в год. Ставка процента в экономике составляет r = 5% в год. Определите, по какой цене следует покупать машину, если:

а) машина будет работать вечно и приносить доход в конце каждого года;

б) машина будет работать вечно и приносить доход непрерывно;

в) доход непрерывен, но производительность машины будет непрерывно уменьшаться по закону: 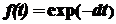, где коэффициент износа d = 0.1.