Практикум « Установление цены на уровне текущих цен»
Допустим, необходимо определить цену нового двухкамерного холодильника "Атлант". Известно, что на рынке конкурентом предприятия продается подобный холодильник "Снежная королева" по цене 200.000 рублей. Назовем холодильник, с которым будет сравниваться "Атлант" и на цену которого будет ориентироваться предприятие в процессе ценообразования, базовым изделием. Процесс установления цены на "Атлант" складывается из нескольких этапов.
1-ый этап. Выбирают качественные параметры холодильников, которые определяют их потребительские свойства. Допустим выбрано 7 таких параметров. Они представлены в гр.1 таблицы.
2-ой этап. Подбираются несколько независимых экспертов (а лучше, если будет проведено анкетирование потребителей, хотя это достаточно дорого). Допустим выбрано 4 группы экспертов.
3-ий этап. Экспертов просят оценить, какой параметр из семи представленных является наиболее важным, какой - чуть менее, какой - еще менее важен и т.д. Такой процесс называется ранжированием. В данном случае экспертов просят провести "обратное ранжирование", т.е. поставить самый важный параметр на 7-ое место, а наименее важный - на 1-ое место. Далее, из результатов по каждому параметру выводится "среднее место". Результаты данного этапа занесены в гр.2
4-ый этап. Экспертов просят оценить по 10-балльной шкале каждый параметр базового изделия ("Снежная королева") и изделия предприятия ("Атлант"). Рассчитывается "средний балл" по каждому параметру для обоих изделий, результаты расчета представлены в гр.3 и 4.
5-ый этап. Определяем бальную оценку параметров холодильников "Снежная королева" и "Атлант" с учетом важности параметров по формуле:
Балльная оценка параметра изделия с учетом важности данного параметра для потребителей = Средний показатель важности параметра для потребителя * Средняя оценка параметра изделия.
6-ой этап. Определяется цена одного балла. Для этого необходимо известную цену базового холодильника разделить на общую сумму набранных этим холодильником баллов.
| 200.000 | ||||
| Цена 1 балла | = | --------------- | = | 1.214 руб. |
| 164.782 |
7-ой этап. Когда известна цена одного балла, можно рассчитать цену каждого параметра холодильника "Атлант" умножением по строкам гр. 9 с ценой 1 балла. Цена каждого параметра холодильника "Атлант" определена в гр. 10
8-ой этап. Определение цены. Ее можно определить двумя способами:
а) менее точный способ расчета цены без учета важности параметров:
Цена = Цена базового изделия * (Сумма баллов изделия предприятия / Сумма баллов базового изделия)
| 46,375 | ||||||
| Цена холодильника | = | 200.000 | * | ----------- | = | 243.200 руб. |
| 38,126 |
б) более точный способ расчета цены с учетом важности параметров:
Цена = Балльная оценка изделия предприятия с учетом важности параметров * Цена одного балла
| Цена холодильника | = | 184,798 | * | 1.214 | = | 224.345 руб. |
| Параметры и их важность | Бальная оценка изделия | Цена парам. | |||||||
| Параметры | Важность параметра | базового | предприятия | с учетом важности | тыс. руб. | ||||
| эксп. | средн. | эксп. | средн. | эксп. | средн. | базов. | предпр. | ||
| 1. Надежность | 4,6 6,7 6,6 5,6 | 5,875 | 6,1 6,5 6,7 6,7 | 6,500 | 5,4 5,0 4,5 4,6 | 4,875 | 38,188 | 28,641 | 34,77 |
| 2. Долговечность | 2,2 5,6 5,7 4,5 | 4,500 | 3,4 3,4 4,3 3,4 | 3,625 | 5,4 4,1 3,4 5,6 | 4,625 | 16,313 | 20,813 | 25,27 |
| 3. Емкость | 6,3 6,0 6,5 6,7 | 6,375 | 6,9 6,7 6,7 7,7 | 7,000 | 8,8 7,8 9,8 7,8 | 7,875 | 44,625 | 50,203 | 60,94 |
| 4. Емкость морозильной камеры | 4,9 2,4 4,4 4,3 | 4,000 | 5,4 5,6 5,6 5,4 | 5,500 | 6,1 6,6 6,6 6,7 | 6,500 | 22,000 | 26,000 | 31,56 |
| 5. Дизайн | 1,1 1,1 1,1 1,2 | 1,125 | 2,6 2,3 3,4 3,2 | 2,875 | 5,4 5,4 4,5 4,4 | 4,750 | 3,234 | 5,344 | 6,49 |
| 6. Удобство расположения полок | 2,4 2,3 3,2 2,1 | 2,500 | 4,6 4,5 5,4 4,5 | 4,750 | 9,9 8,9 8,9 9,8 | 9,375 | 11,875 | 23,438 | 28,45 |
| 7. Вес ящиков | 4,6 4,2 2,3 3,4 | 3,625 | 7,3 8,8 7,7 7,7 | 7,875 | 8,9 7,9 8,8 7,9 | 8,375 | 28,547 | 30,359 | 36,86 |
| Сумма | 38.125 | 46.375 | 164,782 | 184.798 | 224,34 |
Практикум «Оптимизация задач логистических операций материального потока»
Задача 1
Требуется провести оптимизацию размещения материально-технических ресурсов на складах.
Используя экономико-математические методы линейного программирования, находят оптимальный вариант закрепления поставщиков продукции за складами.
Например, имеется 3 производителя однородной продукции,4 склада (распределительных центра - РЦ) для этой продукции и 5 потребителей продукции (см. задание).
Для решения задачи требуется:
1. Составить по исходным данным матрицу и решить ее распре
делительным методом линейного программирования.
2. Закрепить поставщиков однородной продукции за распредели
тельными центрами (РЦ).
3. Произвести расчет стоимости доставки и объемов поставок
продукции на РЦ.
4. Произвести расчет средней стоимости доставки груза для
участников логистической цепочки по следующей методике:
С =QS,
где С - стоимость доставки в у.е.;
Q- объем продукции определенного поставщика в тоннах;
S- существующая стоимость доставки 1 тонны продукции для каждого поставщика.
∑С=С1 +С2 +С3 …+Сn
где - ∑С общая стоимость доставки Qmпродукции;
Сср=∑С/∑Q
где Сср - средняя стоимость доставки 1 т продукции.
5. Вычертить логистическую цепочку между распределительными центрами и поставщиками продукции, исходя из оптимального варианта решенной задачи.
Задача2
Необходимо оптимизировать технологию перемещения материально-технических ресурсов.
Для решения задачи требуется:
1. По исходным данным составить матрицу размером по количеству
поставщиков и потребителей однородной продукции.
2. Получить оптимальный вариант.
3. Разработать маршруты материальных потоков.
4. Рассчитать маршруты по следующей методике:
1) определить время работы подвижного состава (ПС) на маршруте Тм,ч:
Тм=Тн-∑l0 /Vm,
где Тн- время работы ПС, ч;
∑l0 - суммарный нулевой пробег ПС, км;
Vm- техническая скорость ПС, км/ч;
2) рассчитать время движения ПС tдв, ч:
tдв=Lм /Vm
где LM - длина маршрута материального потока, км,
3) рассчитать время одного маршрута
tM = tдв +tn-pх n
где tn-p - время на погрузочно-разгрузочные операции, ч;
п - количество погрузок-разгрузок (заездов) на маршруте;
4) рассчитать количество маршрутов за смену (т.е. за время работы на маршруте):
Z=Тм/tM
где Тм - время работы на маршруте, ч;
tM - время работы на одном маршруте, ч.
5. Рассчитать коэффициент использования пробега ПС за смену и за один маршрут βсм , βм:
βсм = ∑lгр/ (l0+lгр+ lx),
где βсм-суммарный груженый пробег ПС за смену, км;
I0 - нулевой пробег автомобиля, км;
1гр- груженый пробег автомобиля за смену, км;
1Х- пробег автомобиля без груза за смену, км;
6. Рассчитать потребное количество ПС (автомобилей) для выполнения заданного объема перевозок А:
A=∑Q/PQ,
где ∑Q- суммарный объем перевозок по одному маршруту за смену, т; Pq- производительность ПС, т,
Pq=ZnусqH,
где Z - число маршрутов за смену;
п - число заездов на маршруте;
ус - коэффициент использования грузоподъемности ПС (берется по прейскуранту в зависимости от класса перевозимого груза);
qH - номинальная грузоподъемность ПС (берется по технической характеристике ПС), т.
7. Определить суммарное количество ПС для заданного объема перевозок:
А =А1+А2+..Ai
где А1 - количество ПС по первому маршруту и т.д.
Задача3
Требуется решить задачу о назначениях. Имеется п поставщиков и п потребителей. Необходимо с максимальной производительностью в минимальные сроки выполнить доставку груза. Известно, что 1-й поставщик, закрепленный заj-м потребителем, будет приносить доход Cij. Требуется так осуществить доставку продукции, чтобы максимизировать суммарный доход.
Для решения поставленных задач необходимо использовать логистический подход в управлении материальным потоком, т.е. интегрировать отдельные участки логистического процесса в единую систему, способную быстро и экономично доставить необходимый товар (груз, продукт) в нужное место.
Сложность заключается в том, что в рамках единой системы необходимо объединить различных собственников (в нашем случае - производителя, транспорт, склады и потребителя), т.е. субъектов с различными экономическими интересами. Для этого следует заинтересовать всех участников логистического процесса путем постановки ряда задач, результатом решения которых является общая прибыль без каких-либо дополнительных вложений. Логистическая оптимизация материального потока позволяет снизить совокупные затраты на товародвижение.
Результат достигается за счет решения вышеперечисленных задач. Логистическая оптимизация процесса доведения материально-технических ресурсов до конечного потребителя предполагает наличие тесных партнерских связей между всеми участниками логистического процесса, т.е. работу на общий результат. В результате регулирования механизма экономических взаимоотношений участников возникает интегрированный совокупный сквозной материальный поток, для оптимизации которого необходимо решить экономическую, математическую и технологическую задачи.
В нашем случае участниками логистического процесса являются поставщики продукции (производители), транспорт, склады и потребители этой продукции. В процессе оптимизации материального потока решаются следующие задачи:
1) задача на минимальную стоимость доставки продукции;
2) задача на минимум затрат при планировании технологии
перевозок;
3) задача на минимум времени выполнения заказа при
максимальной производительности.
При решении 1 -й задачи оптимизация достигается за счет оптимального закрепления производителей продукции за складами, что дает снижение средней стоимости доставки готовой продукции на склады, и каждый участник логистической цепочки получает дополнительный процент прибыли.
Решение 2-й, технологической, задачи оптимизации траектории движения материального потока снижает транспортные затраты за счет сокращения непроизводительных пробегов подвижного состава.
3-я задача оптимизации дает возможность добиться максимальной производительности при минимальных затратах времени за счет оптимизации подачи ПС от складов в пункты потребления продукции.
Дополнительная прибыль при снижении совокупных транспортных затрат в данном случае происходит за счет 3-х факторов:
1) снижение средней стоимости доставки продукции от
производителя на склады;
2) снижение непроизводительных пробегов транспорта;
3) сокращение времени выполнения заказа.
Задача 4
Имеются три производителя продукции (обозначаются буквойП с соответствующим индексом – П1П2, П3), четыре склада (обозначены буквой A с соответствующим индексом – А1, А2, A3, A4; в дальнейшем они будут выступать в роли поставщиков продукции), пять потребителей готовой продукции (соответственно В1, В2, В3, В4, В5). Имеются объемы продукции, расстояния между участниками логистической цепочки и стоимости доставки продукции.
Требуется провести оптимизацию совокупного материального потока для получения дополнительной прибыли за счет снижения затрат на каждом участке движения материального потока по логистической цепочке.
Решение:
В первую очередь, необходимо закрепить производителей за распределительными центрами РЦ (складами), что даст оптимальный вариант доставки продукции, т.е. минимальную стоимость.
Существующая схема доставки продукции следующая: производитель П1доставляет продукцию на склад А1в объеме 150 т; производитель П2- на склад А3в объеме 80 т, на склад А2 - в объеме 120 т; производитель П3 - на склад А4в объеме 100 т. Общий объем материального потока составляет 450 т. Имеются стоимости доставки продукции до каждого склада.
Для оптимизации поставленной задачи необходимо составить матрицу и решить ее с помощью математического метода линейного программирования.
В табл. 2.1 представлен оптимальный вариант закрепления производителей за РЦ.
Таблица2.1 Матрица оптимизации материального потока
| РЦ | Производители | ∑A, | ||||||
| П1 | П2 | Пз | ||||||
| Ai | ||||||||
| А2 | ||||||||
| А3 | -2 | |||||||
| А4 | ||||||||
| ∑П |
Для решения задачи требуется:
1. Рассчитать первоначальную (существующую) стоимость доставки продукции на склады:
Ссущ =150 х 5 +120х7 +80х9 +100х12=3510 у.е.
Сср = С сущ/ Q =3510/450=7,8 у.е.
2. Рассчитать оптимизированную стоимость доставки продукции:
Сопт=130х4 + 20х6 + 180х3 + 80х4 + 30х5 + 70х6 = 2070у.е.;
Ссропт=2070/450 = 4,6 у.е.
Из расчета видно, что затраты доставки продукции на склады снизились на 1440 у.е., т.е. каждый производитель вместо 7,8 у.е. заплатит за 1 т 4,6 у.е.
Схематически это будет выглядеть следующим образом (рис. 2.1, 2.2).
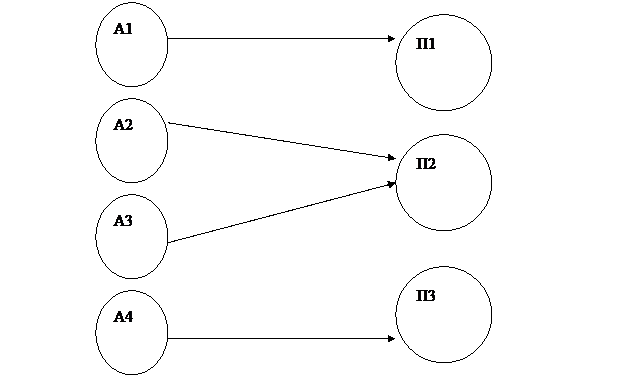
Рис. 2.1. Существующая схема доставки продукции
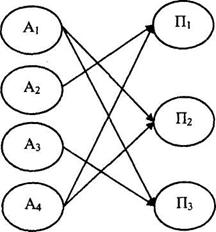
Рис. 2.2. Оптимизированная схема доставки продукции
Ссуш = 3 510 у.е.; Conm= 2 070 у.е.;
Сср= 7,8 у.е. за тонну груза; Ссропт= 4,6 у.е. за тонну груза; ∆С = Ссущ - Сопт= 1440 у.е.
Задача5
Необходимо со складов (теперь они уже являются поставщиками) отправить продукцию потребителям таким образом, чтобы оптимизировать суммарные транспортные расходы.
Есть 4 поставщика продукции и 5 потребителей; имеются объемы поставок, объем потребности в продукции, расстояния между поставщиками и потребителями.
Составить транспортную задачу при условии, что поставщик А1должен отправить груз потребителю В4 в размере 100 т и потребителю В2-150 т; А2- потребителю В1- 120 т; А3 - потребителю В3 - 80 т; А4- потребителю В5 - 100 т.
Необходимо составить матрицу и получить оптимальный вариант.
Матрица оптимального варианта материального потока
| Потребители | Поставщики | ∑A, | ||||||||||||||||||||||||||
| А1, | А2 | Аз | А4 | |||||||||||||||||||||||||
| В1, | ||||||||||||||||||||||||||||
| в2 | ||||||||||||||||||||||||||||
| Вз | ||||||||||||||||||||||||||||
| в4 | ||||||||||||||||||||||||||||
| в5 | ||||||||||||||||||||||||||||
| ∑Bj | ||||||||||||||||||||||||||||
Для решения задачи требуется:
1. Рассчитать непроизводительный пробег автомобиля до оптимизации:
lсущ=W/Q
lсущ=(100х20+ 50х21 +120х12 +80х25 +100х21): 450=19 км
___
где 1сущ - существующий непроизводительный пробег одного автомобиля;
W— транспортная работа в т.км (фиктивная);
Q - объем перевозок в тоннах.
2. Рассчитать непроизводительный пробег автомобиля после оптимизации:
lопт=90х12 + 30х10 + 50х10 + 80х8 + 30х10 + 70х8 + 60х8 + 40х9
= 9,3 км;
∆l= 19-9,3 = 9,7 км.
3. Рассчитать сокращение непроизводительного пробега всех автомобилей на заданный объем материального потока:
∑lопт= Qlопт
∑lопт = 450 • 9,7 = 4365 км.
Если принятьстоимость пробега 1 кмS = 0,35 у.е., то общая экономия составит
Э = 0,35 х 4365 = 1527,75 у.е.
Задача 5
Рассчитайте оптимальный размер заказа ДВП (древесно-волокнистой плиты) твердой, если издержки выполнения заказа составляют 2 руб./м2; потребность в пиломатериалах - 3000 м2; затраты на хранение составляют 1 руб./м2.
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Определение потребности в материале. | S = 3000 м2 (из условия задания) | |
| Определение издержек выполнения заказа. | С0= 2 руб./м2 (из условия задания) | |
| Определение затрат на хранение единицы заказываемого материала. | / = 1 руб./м2 (из условия задания) | |
| Расчет оптимального размера заказа по формуле Уилсона. | 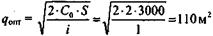 |
Ответ: оптимальный размер заказа ДВП 110 м2.
Задача 6.
Рассчитайте интервал времени между заказами, если потребность в ДВП в 2007 г. составляет 3000 м2, а оптимальный размер заказа -110 м2
| № | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| п/п | ||
| Определение количества рабочих дней в году. | Количество рабочих дней N в 2007 г. принимаем равным 250. | |
| Определение потребности в материале. | Потребность в материале S= 3000 м2 (из условия задания). | |
| Определение оптимального размера заказа. | Оптимальный размер заказа qom = 110м2 (из условия задания). | |
| Расчет интервала времени между заказами. | 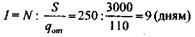 По согласованию с экспертами данный интервал времени можно скорректировать до 10 рабочих дней, тогда поставки будут осуществляться 1 раз в 2 недели. По согласованию с экспертами данный интервал времени можно скорректировать до 10 рабочих дней, тогда поставки будут осуществляться 1 раз в 2 недели. |
Ответ: расчетный интервал поставки составляет 9 рабочих дней и может быть скорректирован до поставок 1 раз в 2 недели.
Задача 7
Рассчитайте оборот склада за месяц работы при следующих условиях: через склад прошло 20000 т груза, причем 8000 т хранилось 5 дней; 5000 т груза хранилось 7 дней, а 7000т хранилось 10 дней.
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| 1 Определение расчетного периода времени. | Расчетный период Т = 30 дням (изусловия задания). | |
| Определение общего количества груза, прошедшего через склад за расчетный период. | Общее количество груза, прошедшего через склад за 30 дней, Q= 20000 т (из условия задания). | |
| Расчет общего количества тонно дней хранения за расчетный период. | Общее количество тонно-дней хранения: 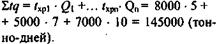 | |
| Расчет среднего срока хранения грузов на складе. | Средний срок хранения: 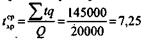 | |
| Расчет оборота склада за расчетный период. | Оборот склада: 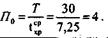 |
Задача 8
Рассчитайте оборот склада за месяц работы при следующих условиях: через склад прошло 20000 т груза, причем 8000 т хранилось 5 дней; 5000 т груза хранилось 7 дней, а 7000т хранилось 10 дней.
| № | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| п/п | ||
| Определение расчетного периода времени. | Расчетный период Т= 30 дням (изусловия задания). | |
| Определение общего количества груза, прошедшего через склад за расчетный период. | Общее количество груза, прошедшего через склад за 30 дней, Q= 20000 т (из условия задания). | |
| Расчет общего количества тонно- дней хранения за расчетный период. | Общее количество тонно-дней хранения:  | |
| Расчет среднего срока хранения грузов на складе. | Средний срок хранения: 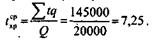 | |
| Расчет оборота склада за расчетный период. | Оборот склада: 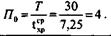 | |
Задача 9
Рассчитайте полезную площадь склада поковок способом нагрузки на 1 м2, если нагрузка на 1 м2 пола составляет 3,5 т, а величина установленного запаса поковок 14000 т.
| № и/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Определение нагрузки на 1 м" пола. | Нагрузка на 1 м2 пола а = 5 т/ м2 (из условия задания). | |
| Определение величины установленного запаса материалов. | Величина установленного запаса формовочных материалов д.™* = 25000 т (из условия задания). | |
| Расчет полезной площади. | Полезная площадь: 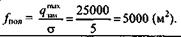 |
Ответ: полезная площадь склада формовочных материалов равна 5000 м2.
Задача 10
Выберите более эффективный вариант системы складирования на основе показателя общих затрат при следующих условиях.
1 вариант. Затраты А, связанные с эксплуатацией, амортизацией и ремонтом оборудования склада, составляют 4,15 млн. руб.; стоимостьоборудования склада С 82,5 млн. руб.; средняя оборачиваемость товара п 20; вес (масса) товара Q, размещенного на складе, 20000 т.
2 вариант. Затраты А, связанные с эксплуатацией, амортизацией и ремонтом оборудования склада, составляют 3,5 млн. руб.; стоимость оборудования Ст склада 90,0 млн. руб.; средняя оборачиваемость товара п 20; вес (масса) товара Q, размещенного на складе, 25000 т.
| № | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| п/п | ||
| Расчет текущих затрат на тонну товара по варианту 1. | Текущие затраты по варианту 1: | |
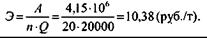 | ||
| Расчет единовременных затрат | Единовременные затраты по варианту 1: 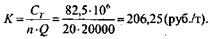 | |
| на тонну товара по варианту 1. | ||
| Расчет общих затрат на тонну | Общие затраты по варианту 1: | |
| товара по варианту 1. | 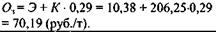 | |
| Расчет текущих затрат на тонну товара по варианту 2. | Текущие затраты по варианту 2: | |
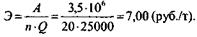 |
Задача 11
Рассчитайте необходимое количество кранов, если за cутки необходимо переработать 600 т груза, производительность кранов составляет 20 т/ч, коэффициент неравномерности поступления груза к =1,2, продолжительность смены 8 ч.
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Определение количества перерабатываемого за сутки груза. | Количество перерабатываемого за сутки груза Q = 600 т. | |
| Определение продолжительности рабочей смены. | Продолжительность рабочей смены -8 ч. | |
| Определение производительности оборудования за смену. | Производительность оборудования за смену: 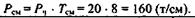 | |
| Определение коэффициента неравномерности поступления груза. | Коэффициент неравномерности поступления груза к = 1,2. | |
| Расчет потребного количества оборудования. | Расчет количества кранов: 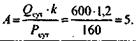 |
Ответ: для выполнения заданного объема работ потребуется 5 кранов.
