Экспоненциальное сглаживание
Возможно, что экспоненциальное сглаживание – это наиболее популярный метод прогнозирования. Он очень прост, требует минимальных исходных данных, обладает высокой точностью и легко адаптируется под конкретные задачи прогнозирования. Метод является вариантом методики расчета скользящих средних, при котором результаты прошлых наблюдений имеют меньший вес, чем результаты новых, более свежих наблюдений за продажами.
Такая схема распределения весовых коэффициентов может быть задана простым уравнением, в котором прогноз на будущий период составляется на основе прогноза предыдущего периода и фактических продаж в текущем периоде:
НОВЫЙ ПРОГНОЗ = a´(ФАКТИЧЕСКИЙ СПРОС) + (1 – a)´(ПРЕДЫДУЩИЙ ПРОГНОЗ)
В этой формуле a – это весовой коэффициент, или сглаживающая постоянная. Коэффициент a варьируется от 0 до 1. Отметим, что все прошлые наблюдения за продажами включены в прогноз предыдущего периода. Таким образом, вся предыдущая история продаж отражена в одном числовом значении прогноза за предыдущий период.
Пример. Допустим, что прогноз спроса в текущем месяце составляет 1000 шт. Фактический спрос в текущем месяце составил 950 шт. Сглаживающая константа составляет a = 0,3. Ожидаемый спрос в следующем месяце определяется по формуле:
Новый прогноз = 0,3´950 + 0,7´1000 = 985 шт.
Этот новый прогноз будет использоваться в формуле для расчета нового прогноза на второй месяц и т.д.
Для удобства расчетов запишем формулу экспоненциального сглаживания в виде следующей модели:
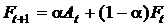 ,
,
где t – текущий временной период; Ft – прогноз продаж на период t; Ft+1 – прогноз продаж на период (t+1); a – константа сглаживания; At – продажи в период t.
Пример. Следующий квартальный временной ряд представляют данные о спросе на продукцию за полтора года:
| Квартал | ||||
| I | II | III | IV | |
| Прошлый год | 1 200 | 1 100 | ||
| Текущий год | 1 400 | 1 000 | F3 = ? |
Нам необходимо построить прогноз на третий квартал текущего года. Допустим, что сглаживающая постоянная a = 0,2. Прогноз предыдущего периода рассчитаем как средний уровень спроса в квартал по данным предыдущего года. Следовательно, А0 = (1200 + 700 + 900 + 1100)/4 = 975. Допустим, что прогноз продаж в прошлом году в среднем соответствовал фактическим продажам, т.е. F0 = А0 = 975.
Тогда прогноз на первый квартал текущего года:
F1 = 0,2´A0 + (1 – 0,8)´F0 = 0,2´975 + 0,8´975 = 975
Прогноз на второй квартал текущего года:
F2 = 0,2´A1 + (1 – 0,8)´F1 = 0,2´1400 + 0,8´975 = 1060
Прогноз на третий квартал текущего года:
F3 = 0,2´A2 + (1 – 0,8)´F2 = 0,2´1000 + 0,8´1060 = 1048
В итоге получаем следующие результаты:
| Квартал | ||||
| I | II | III | IV | |
| Прошлый год | 1 200 | 1 100 | ||
| Текущий год | 1 400 | 1 000 | F3 = ? | |
| Прогноз |
Выбор оптимального значения сглаживающей константы основывается на оценочных суждениях.
§ Чем выше значение константы a, тем большее влияние на прогноз оказывают последние наблюдения за фактическими продажами. В результате модель более гибко и быстро реагирует на изменения в продажах. Однако слишком высокий уровень a делает модель слишком «нервной», слишком чутко реагирующей на любой случайное колебание спроса без учета основной тенденции развития.
§ Чем ниже значение константы a, тем больший вес в прогнозе имеют прошлые наблюдения за фактическими продажами. В виду этого модель реагирует на изменения в тенденциях развития спроса медленнее, с запозданием. При очень низком значение a модель реагирует на изменения спроса крайне медленно и тяжело, что обеспечивает очень «стабильный» прогноз, но делает его крайне неправдоподобным, не похожим на временной ряд.
Наиболее приемлемые значения константы a варьируются в интервале от 0,01 до 0,3. Более высокие значения a могут использоваться при краткосрочном прогнозировании, когда ожидаются какие-то серьезные изменения на рынке. Например, падение продаж, краткосрочные и агрессивные маркетинговые компании, вывод из продуктовой линии некоторых устаревших продуктов, начало продаж нового продукта, когда нет еще достаточной статистики для прогнозирования спроса и пр.
Основное правило при выборе значения константы a: модель должна отображать основную тенденцию в развитии спроса и сглаживать случайные колебания. Такая константа обеспечивает минимальную ошибку прогнозирования.
