Двойственность в теории потребителя

Теорема двойственности:

1. Пусть u() – функция полезности, представляющая ненасыщаемые предпочтения потребителя, определенные на множестве X = R₊^N. Если x* - решение задачи максимизации полезности при ценах p>>0 и доходе I>0, то x* является решением задачи минимизации расходов при u̅ = u(x*). Более того, e(p,u̅) = I

2. Пусть u() – непрерывная функция полезности, представляющая предпочтения потребителя, определенные на множестве X=R₊^N . Если x* - решение задачи минимизации расходов при p>>0 и u̅ = u(0), то х* - решение задачи максимизации полезности при ценах p>>0 и доходе I = e (p, u̅). Более того, v (p,I) = u̅.

Соотношение двойственности для локально ненасыщаемых непрерывных предпочтений:

x(p,I) = H (p, v(p,I));

h(p, u̅) = x(p,e(p, u̅));

v(p, e(p, u̅)) = u̅;

e(p,v(p,I)) = I.

Эффект дохода и замещения. Уравнение Слуцкого.

Изменение цены

Изменение относительных цен ↓		Изменение реального дохода ↓
Покупатель увеличивает спрос на относительно подешевевший товар ↓		Покупатель может как увеличить, так и уменьшить спрос в зависимости от категории товара. ↓
Эффект замены Изменение объема спроса, вызванное только изменением относительной цены товара, при неизменном реальном доходе. (всегда отрицателен!)		Эффект дохода Изменение объема спроса вызванное только изменением реального дохода, при неизменных относительных ценах. (как положителен, так и отрицателен)

Эффект замещения (substitution effect) — изменение структуры потребительского спроса (соотношения средств, выделяемых на покупку разных товаров) в результате изменения цены одного из товаров, входящих в потребительский набор без учета эффекта дохода. Оставшееся увеличение спроса на благо X представляет эффект дохода, так как связано с переходом с одного бюджетного ограничения на другое. Это равносильно увеличению покупательной способности потребителя.

Эффект дохода (income effect) — это воздействие, оказываемое на спрос потребителя за счет изменения реального дохода, вызванного изменением цены блага без учета эффекта замещениия. В случае с нормальными товарами эффект дохода и эффект замещения суммируются, так как происходит расширение потребления нормальных товаров.

Существуют два подхода к определению реального дохода, связанные с именами английского экономиста Дж. Хикса и русского математика и экономиста Е.Е. Слуцкого. Согласно Хиксу, разные уровни денежного дохода, обеспечивающие один и тот же уровень удовлетворения, т.е. позволяющие достигнуть одной и той же кривой безразличия, представляют одинаковый уровень реального дохода. Согласно Слуцкому, лишь тот уровень денежного дохода, который достаточен для приобретения одного и того же набора или комбинации товаров, обеспечивает и неизменный уровень реального дохода. Подход Хикса в большей мере соответствует основным положениям порядковой теории полезности, тогда как подход Слуцкого имеет то преимущество, что позволяет дать количественное решение задачи на основе статистических материалов.

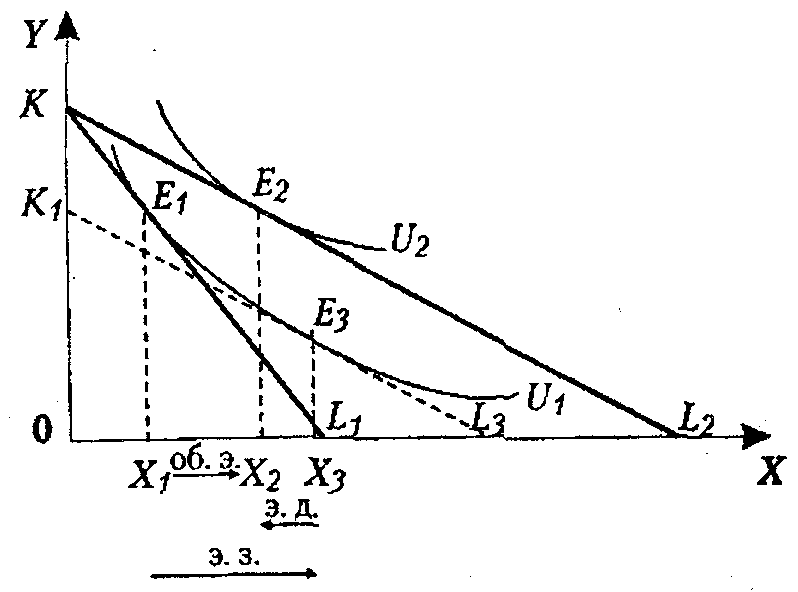
1) 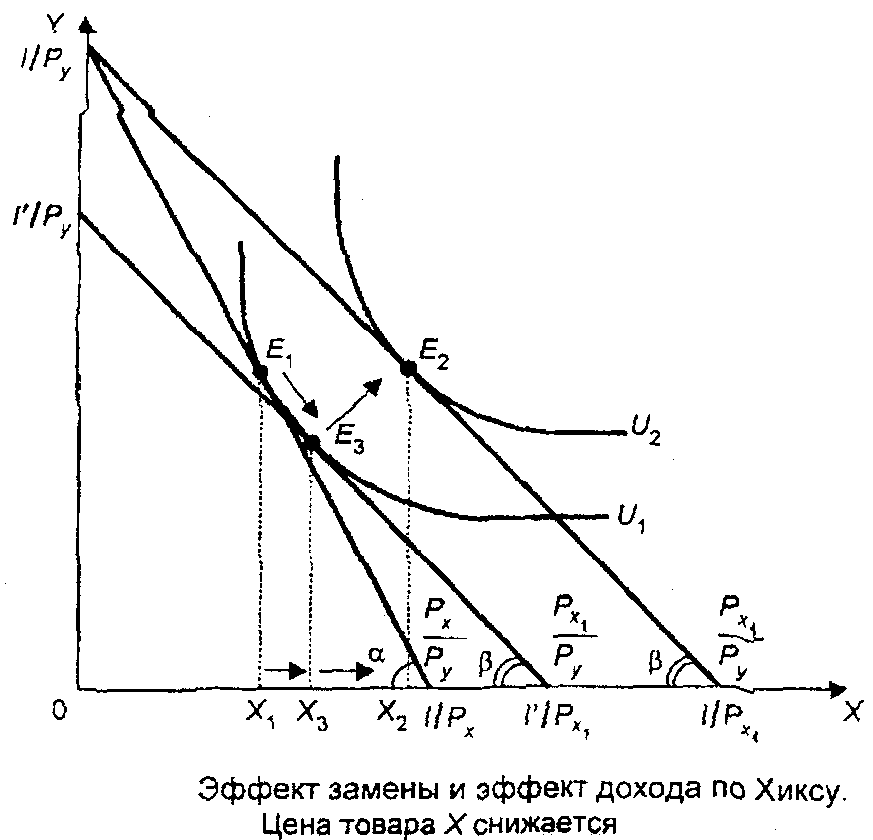Е1 – первоначальное равновесие

2) Изменение цены Х сдвигает бюджетную линию (2) и получаем новую точку равновесия Е2

3) Проводим параллельно линии бюджетного ограничения линию (3) так, чтобы она пересекалась с первоначальной кривой безразличия (сдвигаем вниз)

4) Линия безразличия (3) пересекает Кривую безразличия (1) в точке Ез

Х1Х2 - общий эффект

Х1Х3 - эффект замены

Х2Х3 – эффект дохода

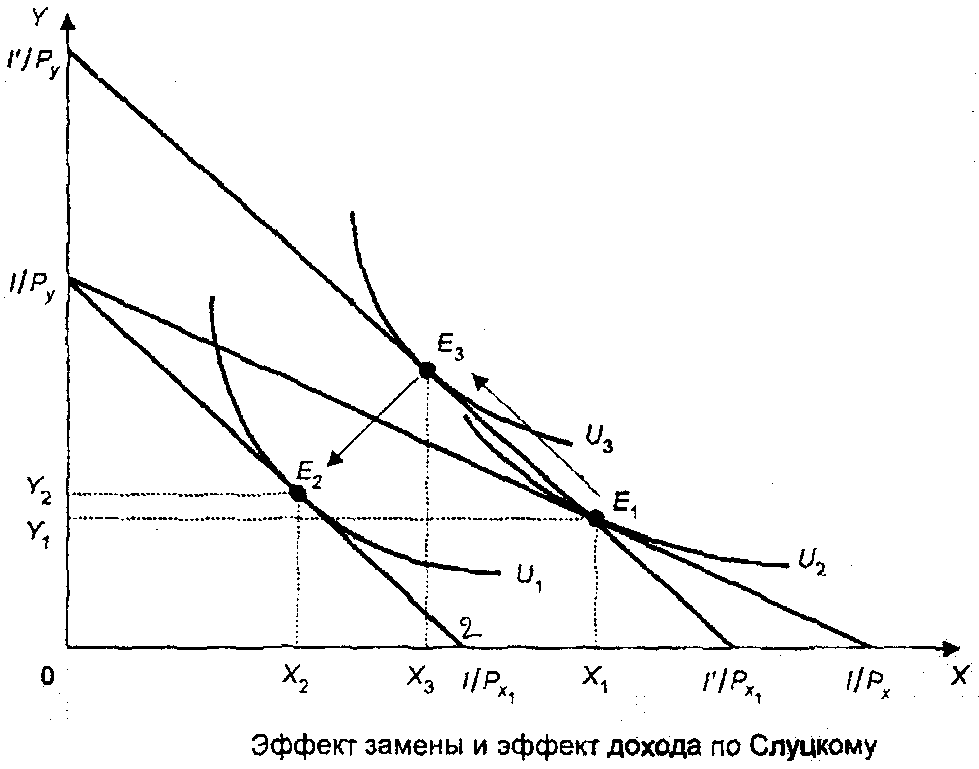
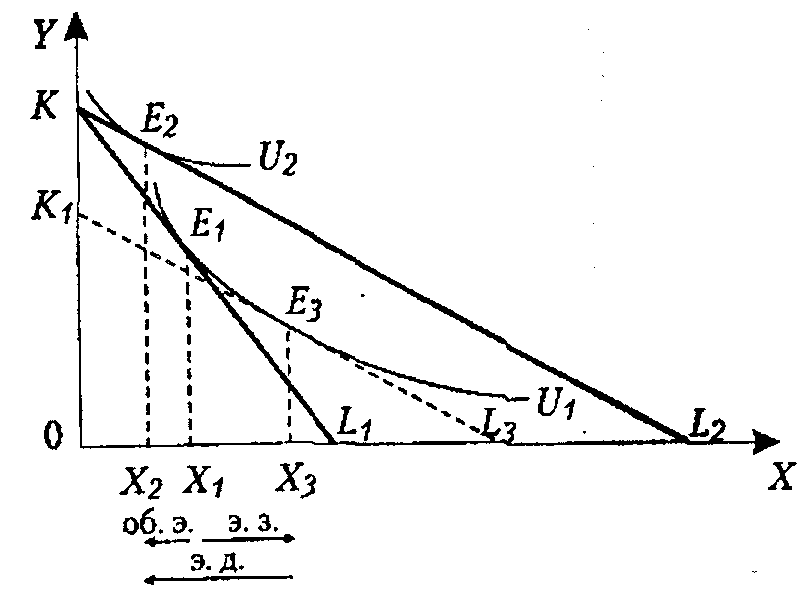
1) Е1 – первоначальное равновесие

2) Изменяется цена Х (растет) и линия бюджетного ограничения сдвигается влево по оси Х – получаем новую точку равновесия Е2

3) Проведем параллельно бюджетной линии линию(3) так, чтобы она прошла через точку первоначального равновесия Е1

4) На линии (3) бюджетного ограничения стоиться НОВАЯ кривая безразличия U3, параллельная U1

5) На пересечении U3 и линии бюджетного ограничения 3 точка нового равновесия – Е3

Х1Х2 - общий эффект

Х1Х3 - эффект замены

Х2Х3 – эффект дохода

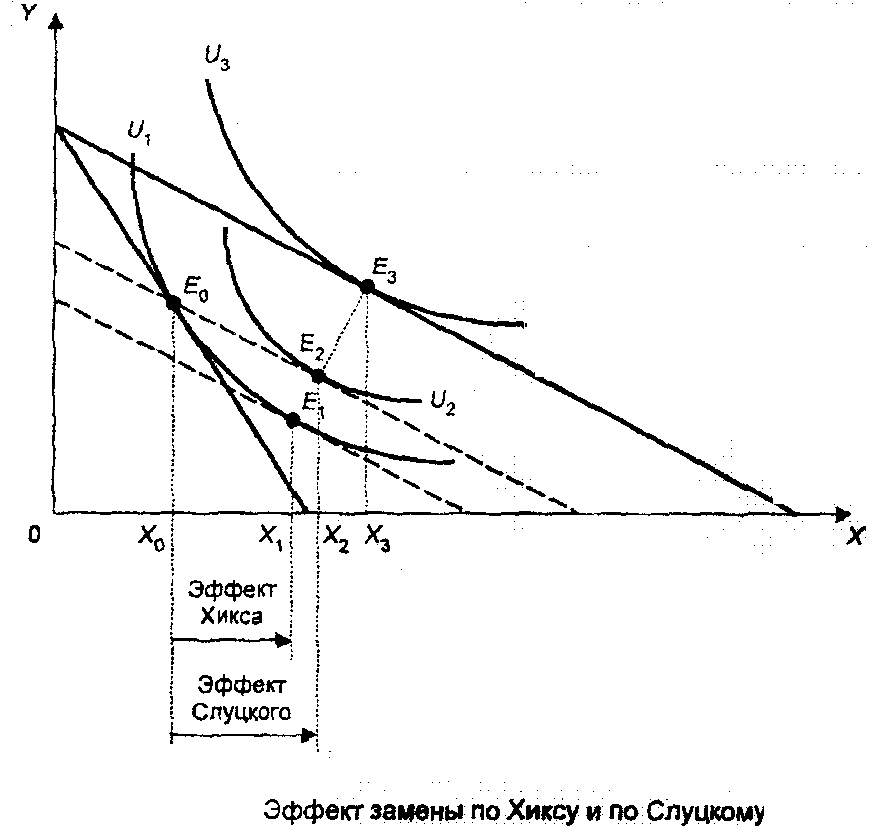
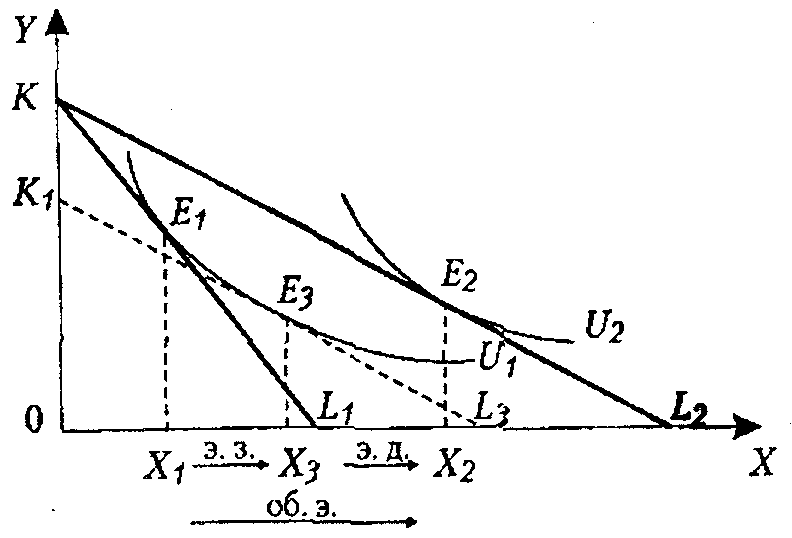
1)Нормальный товар 2) Низкокачественный товар

3).Товар Гиффена – Эффект дохода > эффекта замены. Линия спроса получает положительный наклон.

Товар Гиффена (Giffen good) — это товар, занимающий большое место в бюджете малоимущих потребителей, спрос на который при прочих равных условиях изменяется в том же направлении, что и цена, поскольку эффект дохода превышает эффект замещения.

Уравнение Слуцкого

Для исчисления эффекта дохода и эффекта замещения при изменении цен используется уравнение Слуцкого. Оно отражает тот факт, что общий эффект изменения цены равен алгебраической сумме эффектов дохода и замещения:

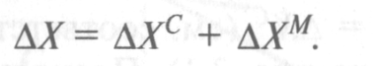
Разделим все члены уравнения на ∆ Р, учитывая, что

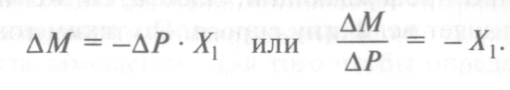, получаем: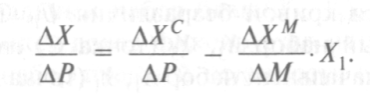

Последняя формула представляет уравнение Слуцкого в форме относительных изменений, где 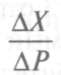показывает, насколько изменилась величина спроса при изменении цены на ∆Р (общий эффект изменения цены); 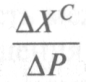показывает, насколько изменилась величина спроса при изменении цены на ∆ Р за счет эффекта замещения при фиксированном реальном доходе (эффект замещения); 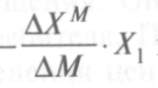показывает, насколько изменилась величина спроса при изменении цены на ∆ Р за счет того, что реальный доход изменился на ∆ M (эффект дохода).

Если предположить, что изменения цены незначительны (∆ Р → 0), то, учитывая, что 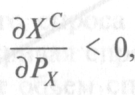, а следовательно, и ∆M→ 0, можем перейти от формулы (3.3) к уравнению Слуцкого в дифференциальной форме:

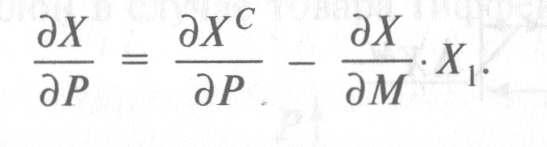
Базой для такого выведения послужит тождество, гласящее, что хиксианский спрос на i-й товар при полезности U тождественно равен маршаллианскому спросу на него при доходе Е(Р, U):

Продифференцировав данное тождество по цене Р:, получаем:

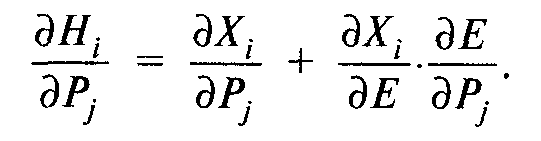Применим лемму Шепарда, по которой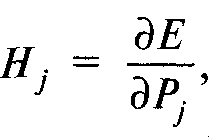

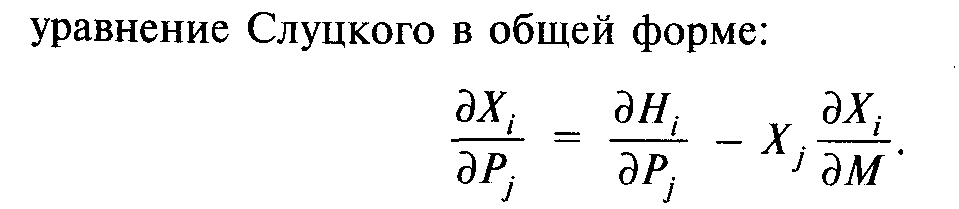
Как видим, им установлена связь хиксианского и маршаллианского спроса на i-й товар, согласно которой изменение последнего есть не что иное, как изменение первого, скорректированное на действие эффекта реального дохода.

Теорема

Пусть u() – непрерывная функция полезности, представляющая строго выпуклые, локально ненасыщаемые предпочтения потребителя, определенные на множестве Х=₊^N Если D(p,I) и H(p,u) – дифференцируемые функции маршалловского и компенсированного спроса, то для всех p̅>>0 и I̅>0 имеет место уравнение Слуцкого.