Выход годного продукции, состоящей из нескольких однотипных компонентов

Усложнение изделий сопровождается увеличением в них числа компонентов с параметрами, влияющими на функции таких сборок. Обеспечение качества изделий, составленных из большого числа однотипных компонентов в большинстве случаев нецелесообразно обеспечивать, контролируя каждый из таких компонентов (подход дорогой и не гарантирует достижения цели) , а часто, как например в сборках микроэлектоники этого сделать и нельзя. Выходом во всех этих случаях является ужесточение требований к возможностям технологических процессов, т.е. к достижению больших значений С_р и С_рk. (улучшение стабильности, снижение дисперсии) и, соответственно к уменьшению доли компонентов, выходящих по отдельным показателям за пределы допусков.

Приведем пример: пусть производится сборка модуля, предназначенного для использования в оконечных устройствах на магистрали мультиплексного канала. Модуль содержит k₁ микросхем, k₂ емкостей и k₃ резисторов. Предположим, что уровни несоответствий одноименных компонентов, полученных в одном техпроцессе одинаков, и они поступают на сборку без селекции. Индекс воспроизводимостипри производстве микросхем С_р1, при производстве емкостей - С_р2, при производстве резисторов - С_р3. Для k₁=5, k₂ =16, k₃ =36, С_р1=1,1, С_р2=1,22, С_р3=1,24 определить, вероятность того, что модуль не содержит несоответствующих единиц.

Решение:

1). Используя формулу 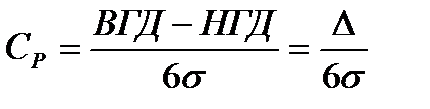, определим поля допуска для каждого компонента:

Δ₁=С_р1•·6σ=1,16•6σ =6,96σ;

Δ₂=С_р2•·6σ=1,22•6σ =7,32σ;

Δ₃= С_р3•·6σ=1,16•6σ =7,44σ;

2) Используя формулу 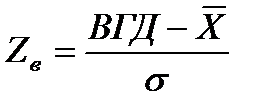( при несмещенном процессе Z_в= Z_н), и учитывая двустороннюю симметрию НДП и ВДП относительно центра распределения, определяем для каждого компонента области под кривой нормального распределения, выходящие за верхнюю и нижнюю границы поля допуска:

Z₁=3,48; Z₁=3,66; Z₁=3,72;

3) Используя таблицу (приложение П7) определяем уровни несоответствия каждого компонента:

q₁ =0,00025•2=0,0005

q₂ =0,00013•2=0,00026

q_{3 =} 0,000104•2=0,000208

4) Определим теперь вероятность того, что модуль не содержит несоответствующих единиц:

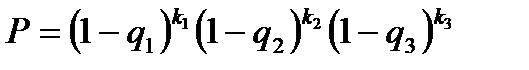= (1-0,0005)⁵•(1-0,00026)¹⁶•(1-0,000208)³⁶=0,9859.

Вывод: Вероятность того, что модуль не содержит компонентов несоответствующего уровня составляет 98,59%.

4.4Основы концепции «6s», как деятельность в параметре процессов Срк =1,5.

Может показаться, что полученное при решении последнего примера значение выхода годных достаточно высокое , но ведь рассматривалась сборка, в которой было всего 5 микросхем, 16 емкостей и 36 резисторов. В современном производстве, например изделий микроэлектроники, сценарий производства полей (array) однотипных микроэлектронных структур сборки является обыденным, однако плотность их размещения на кристалле схемы достигает миллионов и даже миллиардов единиц. Тогда даже очень низкий уровень привносимой процессом дефектности не всегда обеспечивает заданное качество сборки, ведь ожидаемое «количество дефектов» в ней np очевидно зависит не только от дефектности p изделий (см п. 1.3), которая действительно может быть незначительной, но и от числа n однотипных компонентов в составном изделии, а последнее может быть весьма значительным. Действительно для сборки состоящей из kкомпонентов вероятность того, что она не содержит несоответствующих единиц, равна

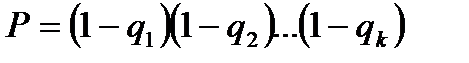
где: q₁, q₂, q_k– уровни несоответствия компонентов или операций в долях единиц;

(1-q₁), (1-q₂), (1-q₃) – вероятность (доля) годных компонентов или операций.

Следовательно, если уровень дефектности получаемых компонентов одинаков, то:

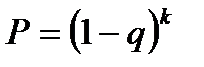
Таким образом, при производстве изделий, состоящих из большого числа однотипных компонентов, должны существенно возрастать требования к технологическому процессу их производства.

Пример : пусть изготавливаются сборки, состоящие из миллиона однотипных ячеек, полученных согласно п. 4.1 в воспроизводимом процессе с С_р=1,666. Определим, используя экспоненциальное распределение (см таблицу Приложения П11) выход годных таких сборок.

Решение:

1). Используя формулу 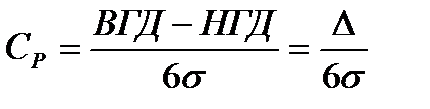= 1.666определим поле допуска производимых компонент: ВДП – НДП= 1,666 * 6s = 9,996 s

2) По таблице нормального распределения (приложение П7 ) найдем, что за пределами допусков в 5s (в обе стороны) находится приблизительно 0,6ppmдефектных компонент (точная величина, которую при современном уровне технологии приходиться теперь рассчитывать равна 0, 57421)

3) По таблице экспоненциального распределения П11 найдем, что выход годного для сборки, в которой содержится «0,6 дефекта» (в сборке из миллиона однотипных компонентов, полученных в достаточно отлаженном процессе с С_р=1,666 «ожидается np=10^{6 *} 0,6ppm= 0,6 дефекта») выход годного составит всего около 55%

Вывод: Выход годных сборок, состоящих из миллиона однотипных ячеек, полученных в одном процессе с достаточно высоким С_р=1,666 равен 55%.

С этой проблемой повышения технологической точности и стабильности процесса связана концепция “шесть сигм”, согласно которой при производстве сложных составных изделий необходимо стремиться к такой технологической точности процесса, при которой среднее квадратическое отклонение σ показателя качества производимой детали в 12 раз меньше его поля допуска, а величина отклонения 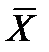от середины поля допуска не превышает (1…1,5) σ. Технологический процесс в этом диапазоне показателей обеспечивает уровень несоответствий ( величины параметров за пределами ВДП и НДП) от 0,000 0034 до 0,000 000 002.

4.5 Функция потерь Тагути.

Концепция качества, разработанная Геничи Тагути состоит в том, что потери для общества, привносимые изделиями при их производстве, транспортировке, в других этапах ЖЦП, возникают даже, если изделие соответствует допускам или требованиям ТУ, но не соответствует заданной величине. Функция потерь («функция потерь Тагути») хорошо представима (посредством разложения в ряд Тейлора) квадратичной функцией типа:

Loss ( L ) = k ( x – m )²

, где k – зависит от потерь общества в точке, в которой переменная как раз превышает допуск. Тогда качество, как функция потерь измеряется в денежных единицах и её математическое ожидание Е будет:

ЕL = Еk ( x – m )² = ks².

Если среднее значение процесса не равно заданной величине m,а равно m + 1.5 s, то необходимо использовать коэффициент С _РК, а не С _Р и ожидание Е( x – m )²будет равно:

Еk( x – m )² = (смещение)²+s² = ( 1,5 s)² + s² = 2.25 s² + s² = 3,25 s².

Таким образом, в отличие только от учета числа дефектов, «выходящих» за пределы допусков за счет увеличения дисперсии s² процесса, функция потерь Тагути концентрирует внимание и на центрировании процесса.

Л5 -а) Причины, цели и задачи внедрения модели системы менеджмента качества (СМК) по ГОСТ Р ИСО 9001- 2008. PDCA-цикл Деминга управления процессами и реализации процессного подхода.