Статистическая обработка результатов исследований

Математическая оценка достоверности количественных показателей, полученных в процессе научного эксперимента, является одновременно оценкой надежности выводов и практических предложений.

Результаты зависят от множества причин и редко повторяются, следовательно, чтобы получить более полное представление о наблюдаемом явлении, надо знать несколько результатов, не менее трех. Совокупность результатов характеризуется одним, называемым средним арифметическим:

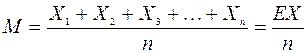, (1)

где М – среднее арифметическое;

Х₁; Х₂; Х₃; … Х_n – соответственно значение 1, 2, 3, … n

результата;

n – число результатов.

Различия между результатами опыта, иначе говоря разброс значений, характеризуются средним квадратическим отклонением (дисперсия), которое вычисляется по формуле:

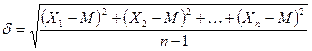, (2)

где - среднее квадратическое отклонение;

Х₁; Х₂; … Х_n – значения результатов 1,2, … n опытов;

М – среднее арифметическое;

n – число опытов.

Степень разброса отдельных результатов характеризуется вариационным коэффициентом:

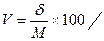, (3)

где V – вариационный коэффициент;

М – среднее арифметическое;

- среднее квадратическое отклонение.

Вариационный коэффициент, выраженный в процентах, является показателем относительного разброса результатов и при нормальном распределении не превышает 45-50%.

Для оценки среднего арифметического вычисляется ошибка среднего арифметического по формуле:

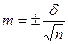, (4)

где m – ошибка среднего арифметического;

- среднее квадратическое отклонение;

n – число опытов.

Величина ошибки среднего арифметического дает пределы, в которых заключается истинное значение исследуемого показателя. Таким образом, полное значение показателя будет:

М + m (5)

Величина ошибки среднего арифметического необходима для установления надежности найденного среднего, критерием которой является соотношение между М и m, т.е.

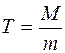
, (6)

где Т – степень надежности среднего арифметического;

М – среднее арифметическое;

m – ошибка среднего арифметического.

Если величина Т > 3, то среднее считается надежным; в случае же, когда T < 3, найденное среднее нельзя использовать для суждения о величине показателя, оно ненадежно. Необходимо в последнем случае продолжить исследования, повышая точность измерений, число опытов. Если исследования проведены на одном и том же объекте, проводится вычисление точности опыта по формуле:

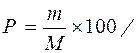, (7)

где Р_т – показатель точности опыта;

m – ошибка среднего арифметического;

М – среднее арифметическое значение.

Показатель точности опыта в случае достаточной достоверности результата не превышает 5%.

Учитывая, что результаты исследований величины, как правило, случайные, а для получения достоверного среднего арифметического значения необходима совокупность измерений, при проведении эксперимента необходимо брать такую повторность опытов, чтобы она при данном разбросе отдельных значений давала вполне определенную задачную точность. Для этого проводится расчет

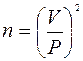, (8)

где n – число исследований (повторность);

V – вариационный коэффициент (по формуле 2.3);

Р_т – показатель точности опыта (2.7).

Таким образом, число необходимых исследований определяется вариабельностью и точностью опыта, которые могут быть не только заданы изначально, но и определены в результате пробных (поисковых) исследований.

Приложение 7

АНКЕТА