Задание №5. Оценка сложных систем в условиях риска и неопределённости

Заказать можно по ссылке http://vk.com/studiplom

Цена работы 300 руб.

Вариант №8

Задание №1. Классификация систем.

Провести классификацию объектов из приложения 1, согласно варианту, занести результаты в таблицы 1.1 – 1.3 (проставив номера объектов в соответствующие клетки).

Таблица 1.3.

По сущности	Технические	Биологи-ческие	Социально-экономические
По внешнему поведению
Открытые	1,2,3,4,5,6,17,18,23,32,34,35,39,42,46,71,74,76,81,82,83,84,86,94,98	20,44,48,49,	7,8,11,12,14,19,21,22,26,27,29,31,33,36,38,40,43,45,47,51,52,53,54,56,58,59,60,61,63,66,68,69,72,75,77,79,85,88,89,91,92,93,97,99,100
Замкнутые (относительно)	9,10,24,25,28,37,41,50,55,57,65,67,70,73,78,80,90,95,96,		13,15,16,30,62,64,87,

Задание 2. Составление анкеты для получения экспертных оценок.

Группа маркетинга автомобильного завода проводит опрос об экспериментальном автомобиле.

Составить образец опросного листа.

Опрос:

Здравствуйте. Меня зовут Юлия, Я представляю группу маркетинга автомобильного завода, которая в интересах будущих покупателей, проводит опрос о новом продукте - экспериментальном автомобиле.

Цель опроса – выявление новых характеристик для покупателей в отношение созданного автомобиля.

Просим Вас принять участие в опросе и ответить на вопросы предлагаемой анкеты. Мы гарантируем полную конфиденциальность Ваших ответов.

Вопрос №1 (вопрос-фильтр). К какому классу можно отнести новый экспериментальный автомобиль? (Нужное подчеркнуть).

1.класс «A» 2.класс «B» 3.класс «C» 4.класс «D» 5.класс «E» 6.класс «F» 7.класс «МИНИВЭНЫ и УПВ» 8.класс «ВНЕДОРОЖНИКИ 9.класс «с кузовом КУПЕ» 10.класс «с открытым кузовом»

………….

Задание 3. Построение дерева целей.

Построение дерева целей

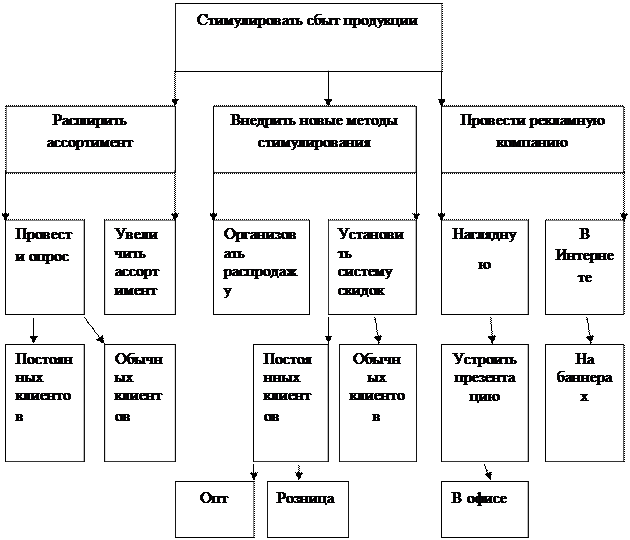
Руководитель фирмы по разработке компьютерных программ поставил задачу перед отделом маркетинга: Стимулировать сбыт продукции в краткосрочной перспективе. Составить дерево целей 5-6 уровней.

Задание №4. Оценка сложных систем в условиях риска и неопределённости

Таблица 4.1.

Оценки показателей каждым из опрошенных экспертов

Показатели	Эксперты
е1
е2
е3
е4
е5
е6

Требуется обосновать сравнение между объектами и выбрать наилучший из них.

Задача состоит в выборе наиболее значимого элемента е_i или группы этих элементов при разных предположениях относительно требований к точности совпадения мнений всех экспертов.

E = { е_i } i = 1,6

К = К₁ К₂…...К₁₀

Оценки рассматриваемых показателей каждым из опрашиваемых экспертов

α^К_j , i = 1,2…6 К = 1,2….10 совпадают с данными таблицы 4.1.

Теперь построим матрицу соответствия.

С этой целью для каждой пары объектов (е_i ,е_j) определим коэффициенты соответствия с_ij, исходя из предположения, что объект е_i предпочтительнее е_j...

Результаты расчётов представлены следующей матрицей С (табл. 4.2).

Таблица 4.2

Матрица С

еj	еi
е1	е2	е3	е4	е5	е6
е1		С12 = 0,6	0,6	0,7	0,6	0,4
сij = е2	0,4		0,5	0,6	0,3	0,3
е3	0,4	0,5		0,8	0,5	0,4
е4	0,3	0,4	0,2		0,2	0,3
е5	0,4	0,7	0,5	0,8		0,7
е6	0,6	0,7	0,6	0,7	0,3

Расчет коэффициента С₁₂.

Задание №5. Оценка сложных систем в условиях риска и неопределённости

Туристическая фирма планирует организовать маршрут по Карелии. Число туристов за сезон ожидается от 5 до 8 тысяч человек. Группы формируются по 20 чел. Необходимо определить число маршрутов а_i, если число туристов k_j. Матрица эффективности имеет вид (тыс. руб.):