Контент- анализ рекламы. 0. Холсти1 для вычисления межкодировочной надежности для номинальных категорий
0. Холсти1 для вычисления межкодировочной надежности для номинальных категорий рекомендует крайне простую формулу:
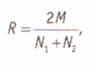 (34)
(34)
где R — показатель надежности (Reliability), М — общее количество совпавших кодовых элементов у двух кодировщиков, N1, N2 — общее количество закодированных элементов у 1-го и 2-го кодировщика соответственно. Например, если в 80 случаях из 100 мнения кодировщиков совпали, то надежность по Холсти составляет:
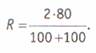
Как dидно, метод понятный, простой в вычислениях, однако имеющий тенденцию завышать надежность кодировки, так как не учитывает, что коды могут совпасть и случайно. допустим, у нас категория имеет две размерности (да — нет). Нетрудно видеть, что, закодировав выборку два раза (имитируя работу двух кодировщиков) с помощью генератора случайных чисел, мы получим надежность, равную примерно 50%. для решения этой проблемы существуют и другие, более сложные формулы. Однако и они не универсальны, поскольку чувствительны к другим аспектам кодировки. Например, в π –индексе2 надежность вычисляется с коррекцией на случайные совпадения:
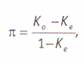 (35)
(35)
где π — оценка надежности, К0 — процент наблюдаемых совпадений кодировщиков, Ке процент ожидаемых совпадений. Недостаток данного индекса состоит в его чувствительности к виду распределения закодированных элементов. Хотя методика его подсчета крайне проста: на первом этапе вычисляется процент ожидаемых совпадений, далее по формуле Холсти вычисляется процент наблюдаемых совпадений. Подставляя эти величины в формулу, мы и получим i-индекс. Например, в нашем гипотетическом примере с чистящими средствами основные рекламируемые выгоды распределились следующим образом (%):

А. Кутлалиев
А. Попов
• цена—ЗО,
• соотношение цена/качество — 25,
• чистящие способности — 15,
• концентрация — 10,
• другое — 10,
• не обнаружено — 10.
Тогда процент ожидаемых совпадений равен 0,205 (0,302 + 0,252 + О,152 + 0,102 + 0,102 + 0,102 = 0,205), а процент наблюдаемых совпадений возьие из предыдущего примера — 80%. Тогда:
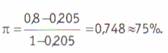
Перро и Лей1 разработали другой подход к коррекции межкодировочной надежности. Эта формула также не свободна от недостатков, в частности, она зависит от количества размерностей в категории. В каноническом виде она выглядит следующим образом:
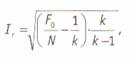 (36)
(36)
где F0 — количество совпавших кодовых элементов, N — общее количество кодовых элементов, к — количество размерностей в категории. Например взяв предыдущие данные, мы получим F0= 80, N = 100, к = 6. Оценка надёжности по Перро — Лею составит:
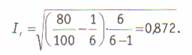
Но, пожалуй, одной из наиболее часто применяемых мер согласия является «каппа Коэна» (Cohen’s kappa)2, вычисляемая по формуле:
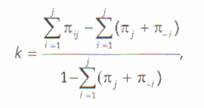 (37)
(37)
где πij — вероятность того, что кодировщик 1 закодирует объект раз-

Глава 11.
