Фигуры и модусы простого категорического силлогизма. Правила фигур. Роль фигур в познании.

В посылках простого категорического силлогизма сред­ний термин может занимать место субъекта или предиката. В за­висимости от этого различают четыре разновидности силлогизма которые называют фигурами. Фигуры силлогизма — это его разновидности, различающиеся положением среднего тер­мина в посылках.

В первой фигуре средний термин занимает место субъекта в большей и место предиката в меньшей посылках.

Посылками силлогизма могут быть суждения, различные по качеству и количеству: общеутвердительные (А), общеотрицатель­ные (Е), частноутвердительные (I) и частноотрицательные (О).

Разновидности силлогизма, различающиеся количе­ственными и качественными характеристиками посылок, на­зываются модусами простого категорического силлогизма. Общее количество вариантов в четырех фигурах 64 модуса, но правильными, т.е. соответствующими всем правилам, являются только 19 из них. По первой фигуре это модусы: ААА, ЕАЕ, АН, ЕЮ.

Помимо общих правил существуют специальные правила фигур.

Правила 1 -й фигуры:

1. Большая посылка — общее суждение.

2. Меньшая посылка — утвердительное суждение.

Первая фигура — наиболее типичная форма дедуктивного умозаключения. Из общего положения, выражающего нередко закон науки, правовую норму, делается вывод об отдельном факте, единичном случае, конкретном лице. Широко применяется эта фигура в судебной практике. Юридическая оценка (квалификация) правовых явлений, применение нормы права к отдельному случаю, назначение наказания за преступление, совершенное конкретным лицом, и другие судебные решения принимают логическую фор­му 1-й фигуры силлогизма.

Во второй фигуре — место предиката в обеих посылках.

Разновидности силлогизма, различающиеся количественными и качественными характеристиками посылок, называются модусами простого категорического силлогизма.

Общее количество вариантов в четырех фигурах 64 модуса, но правильными, т.е. соответствующими всем правилам, являются только 19 из них по второй фигуре: ЕАЕ, АЕЕ, ЕЮ, АОО.

Правила 2-й фигуры: 1. Большая посылка — общее суждение. 2. Одна из посылок — отрицательное суждение.

2-я фигура применяется, когда необходимо показать, что I отдельный случай (конкретное лицо, факт, явление) не может быть I подведен под общее положение. Этот случай исключается из чис­ла предметов, о которых сказано в большей посылке. В судебной I практике 2-я фигура используется для заключений об отсутствии I состава преступления в данном конкретном случае, для опровержения положений, противоречащих тому, о чем говорится в посылке, выражающей общее положение.

В третьей фигуре — место субъекта в обеих посылках.

Посылками силлогизма могут быть суждения, различные по качеству и количеству: общеугвердительные (А), общеотрицатель­ные (Е), частноутвердительные (I) и частноотрицательные (О).

Разновидности силлогизма, различающиеся количе­ственными и качественными характеристиками посылок, на­зываются модусами простого категорического силлогизма.

Общее количество вариантов в четырех фигурах 64 модуса, но правильными, т.е. соответсвующими всем правилам, являются только 19, из них по третьей фигуре: AAI, IAI, All, EAO, ОАО, ЕЮ.

Помимо общих правил существуют специальные правила фигур.

Правила 3-й фигуры: 1. Меньшая посылка — утвердительное суждение.2. Заключение — частное суждение.

Давая только частные заключения, 3-я фигура применяется чаще всего для установления частичной совместимости призна­ков, относящихся к одному предмету. В практике рассуждения 3-я фигура применяется сравнительно редко.

22. Умозаключения из сложных суждений: чисто условное и условно категорическое умозаключение (его модусы и условия правильности).

Чисто условным называется умозаключение, обе по­сылки которого являются условными суждениями. Например:

Если изобретение создано совместным творческим трудом нескольких граждан (р), все они признаются соавторами изобре­тения (q).

Если они признаются соавторами изобретения (г), то порядок пользования правами на изобретение, созданное в соавторстве, определяется соглашением между соавторами (г)

Если изобретение создано совместным творческим трудом нескольких граждан (р), то порядок пользования правами на изоб­ретение, созданное в соавторстве, определяется соглашением между соавторами (г).

В приведенном примере обе посылки — условные суждения, причем следствие первой посылки является основанием второй (q), из которого, в свою очередь, вытекает некоторое следствие (г). Общая часть двух посылок (q) позволяет связать основание пер­вой (р) и следствие второй (г). Поэтому заключение также выража­ется в форме условного суждения. Схема чисто условного умозаключения: (р-> q) л (q-> г)

Вывод в чисто условном умозаключении основывается на правиле: следствие следствия есть следствие основания.

Умозаключение, в котором заключение получается из двух условных посылок, относится к простым. Однако заключение мо­жет следовать из большего числа посылок, которые образуют цепь условных суждений. Такие умозаключения называются сложными.

Условно-категорическим называется умозаключе­ние, в котором одна из посылок — условное, а другая посыл­кой заключение — категорические суждения.

Это умозаключение имеет два правильных модуса: утвержда­ющий и отрицающий.

1) В утверждающем модусе (modus ponens) посылка, выра­женная категорическим суждением, утверждает истинность осно­вания условной посылки, а заключение утверждает истинность следствия; рассуждение направлено от утверждения истинности основания к утверждению истинности следствия.

Например:

Если иск предъявлен недееспособным лицом (р), то суд остав­ляет иск без рассмотрения (q).

Иск предъявлен недееспособным лицом (р).

Суд оставляет иск без рассмотрения (q).

Первая посылка — условное суждение, выражающее связь основания (р) и следствия (q). Вторая посылка — категорическое суждение, в котором утверждается истинность основания (р): иск предъявлен недееспособным лицом. Призназ истинность основа­ния (р), мы признаем истинность следствия (q): суд оставляет иск без рассмотрения.

Утверждающий модус дает достоверные выводы. Он имеет схему: p->q.P q

2) В отрицающем модусе (modus tollens) посылка, выражен­ная категорическим суждением, отрицает истинность следствия условной посылки, а заключение отрицает истинность основания.

Рассуждение направлено от отрицания истинности следствия к отрицанию истинности основания. Например:

Если иск предъявлен недееспособным лицом (р), то суд ос­тавляет иск без рассмотрения (q).

Суд не оставил иск без рассмотрения (1 q).

Неверно, что иск предъявлен недееспособным лицом (1 р).

Схема отрицающего модуса: р -»д. 1д

1р

Нетрудно установить, что возможны еще две разновидности условно-категорического силлогизма: от отрицания истинности основания к отрицанию истинности следствия и от утверждения истинности следствия к утверждению истинности основания.

Однако заключение по этим модусам не будет достоверным. Таким образом, из четырех модусов условно-категорического умозаключения, исчерпывающих все возможные комбинации по­сылок, достоверные заключения дают два: утверждающий и отри­цающий. Они выражают законы логики и называются правильны­ми модусами условно-категорического умозаключения. Эти моду­сы подчиняются правилу: утверждение основания ведет к утверждению следствия и отрицание следствия — к отрица­нию основания. Два других модуса достоверных заключений не дают. Они называются неправильными модусами и подчиняются правилу, отрицание основания не ведет с необходимостью к отрицанию следствия и утверждение следствия не ведет с необходимостью к утверждению основания.

23. Умозаключения из сложных суждений: разделительно-категорическое умозаключение (его модусы, правила) и условно-разделительное умозаключение (понятие конструктивной и деструктивной диллем).

Разделительно-категорическим называется умозак­лючение, в котором одна из посылок — разделительное, а другая посылка и заключение — категорические суждения.

Простые суждения, из которых состоит разделительное (дизъюнктивное) суждение, называются членами дизъюнк­ции, или дизъюнктами. Например, разделительное суждение «Облигации могут быть предъявительскими или именными» состо­ит из двух суждений — дизъюнктов: «Облигации могут быть предъявительскими» и «Облигации могут быть именными», соеди­ненных логическим союзом «или».

Утверждая один член дизъюнкции, мы с необходимостью должны отрицать другой и, отрицая один из них, — утверждать другой. В соответствии с этим различают два модуса разделительно-категорического умозаключения: утверждающе-отрицающий и отрицающеутверждающий.

● В утверждающе-отрицающем модусе (modus ponendo tollens) меньшая посылка, категорическое суждение, утверждает один член дизъюнкции, заключение — также категорическое суждение — отрицает другой ее член. Например:

Облигации могут быть предъявительскими (р) или именными (q).

Данная облигация предъявительская (р).

Данная облигация не является именной (q).

Схема утверждающе-отрицающего модуса →

V — символ строгой дизъюнкции.

Заключение по этому модусу всегда достоверно, если соблюдается правило: большая посылка должна быть исключающее-разделительным суждением, или суждением строгой дизъюн­кции. Если это правило не соблюдается, достоверного заключе­ния получить нельзя. В самом деле, из посылок «Кражу совершил К. или Л.» и «Кража совершена К.» заключение «Л. кражу не совер­шал» с необходимостью не следует. Возможно, что Л. также при-частен к совершению кражи, является соучастником К.

● В отрицающе-утверждающем модусе (modus tollendo ponens) меньшая посылка отрицает один дизъюнкт, заключение утверждает другой. Например:

Облигации могут быть предъявительскими (р) или именными (q).

Данная облигация не является предъявительской (1 р).

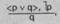Данная облигация именная (q).

Схема отрицающе-утверждающего модуса →

< > — символ закрытой дизъюнкции.

Утвердительный вывод получен посредством отрицания: отри­цая один дизъюнкт, мы утверждаем другой. Заключение по этому модусу всегда достоверно, если соблюдается правило: в большей посылке должны быть перечис­лены все возможные суждения — дизъюнкты, иначе говоря, боль­шая посылка должна быть полным (закрытым) дизъюнктивным высказыванием. Применяя неполное (открытое) дизъюнктивное высказывание, достоверного заключения получить нельзя.

Условно-разделительный силлогизм.Умозаключение, в котором одна посылка условное, а другая — разделительное суждения, называется условно-разделительным, или лемматическим (от лат. — предположе­ние). Разделительное суждение может содержать две, три и боль­шее число альтернатив, поэтому лемматические умозаключения делятся на дилеммы (две альтернативы), трилеммы (три альтер­нативы) и т.д.

Рассмотрим на примере дилеммы структуру и виды условно-разделительного умозаключения. Различают два вида дилемм: конструктивную (созидательную) и деструктивную (разрушитель­ную), каждая из которых делится на простую и сложную.

В простой конструктивной дилемме условная посылка содержит два основания, из которых вытекает одно и то же след­ствие. Разделительная посылка утверждает оба возможных осно­вания, заключение утверждает следствие. Рассуждение направле­но от утверждения истинности оснований к утверждению истинно­сти следствия.

Схема простой конструктивной дилеммы:

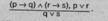
Если обвиняемый виновен в заведомо незаконном задержа­нии (р), то он подлежит уголовной ответственности за преступле­ние против правосудия (г); если он виновен в заведомо незакон­ном заключении под стражу (q), то он также подлежит уголовной ответственности за преступление против правосудия (г).

Обвиняемый виновен или в заведомо незаконном задержа­нии (р) или в заведомо незаконном заключении под стражу (q).

Обвиняемый подлежит уголовной ответственности за преступ­ление против правосудия (г).

В сложной конструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка утверждает оба возможных следствия. Рассуждение направлено от утверждения истинности оснований к утверждению истиннос­ти следствий.

Схема сложной конструктивной дилеммы:

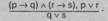
В простой деструктивной дилемме условная посылка со­держит одно основание, из которого вытекает два возможных следствия. Разделительная посылка отрицает оба следствия, зак­лючение отрицает основание. Рассуждение направлено от отри­цания истинности следствий к отрицанию истинности основания.

Схема простой деструктивной дилеммы:

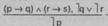
Если Н. совершил умышленное преступление (р), значит, в его действиях был прямой (q) или косвенный умысел (г).

Но в действиях Н. не было ни прямого (q), ни косвенного умысла (г).

Преступление, совершенное Н., не является умышленным (р).

В сложной деструктивной дилемме условная посылка со­держит два основания и два следствия. Разделительная посылка отрицает оба следствия, заключение отрицает оба основания. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности оснований.

Схема сложной деструктивной дилеммы:

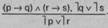
Если предприятие является арендным (р), то оно осуществляет предпринимательскую деятельность на основе взятого им в арен­ду имущественного комплекса (q); если оно является коллектив­ным (г), то осуществляет такую деятельность на основе находяще­гося в его собственности имущества (s).

Данное предприятие не осуществляет свою деятельность ни на основе взятого в аренду имущественного комплекса (1 а), ни на основе находящегося в его собственности имущества (Is).

Данное предприятие не арендное (1 р) или не коллективное (1 г).

24. Сокращенный силлогизм (энтимема). Сложный и сложносокращенный силлогизмы (полисиллогизм, сорит, эпихейрема).

Индуктивные умозаключения: определение, особенности, структура. Полная и неполная индукция. Особенности популярной индукции. Факторы, влияющие на повышение степени вероятности выводов популярной индукции.

В зависимости от полноты исследования различают полную и неполную индукцию. Полная индукция - это умозаключение, в котором общее заключение делается на основе изучения всех предметов и явлений данного класса. В этом случае рассуждение имеет следующую схему:

S 1 - Р

S 2 - Р Только S 1 , S 2 , S 3 , ... S n составляют класс К

S 3 -Р Каждый элемент К - Р

S n - Р

Полная индукция дает достоверное знание, так как заключение делается только о тех предметах или явлениях, которые перечислены в посылках. Но область применения полной индукции весьма ограничена. Полную индукцию можно применить, когда появляется возможность иметь дело с замкнутым классом предметов, число элементов в котором является конечным и легко обозримым. Она предполагает наличие следующих условий:

● точное знание числа предметов или явлений, подлежащих изучению;

● убеждение, что признак принадлежит каждому элементу класса;

● небольшое число элементов изучаемого класса;

● целесообразность и рациональность.

Возьмем для логического анализа следующие правила русского языка.

Именительный падеж выражает грамматические отношения между словами.

Родительный падеж выражает грамматические отношения между словами.

Дательный падеж выражает грамматические отношения между словами.

Винительный падеж выражает грамматические отношения между словами.

Творительный падеж выражает грамматические отношения между словами.

Предложный падеж выражает грамматические отношения между словами.

Именительный, родительный, дательный, винительный, творительный, пред ложный - падежи русского языка

Следовательно, все падежи русского языка выражают грамматические отношения между словами

В данном примере перечислен весь класс падежей. Поэтому общий вывод, который имеет непосредственное отношение к каждому падежу в отдельности, является объективным и истинным. Однако в большинстве случаев человеку приходится иметь дело с такими однородными фактами, количество которых не ограничено или которые не все доступны в настоящее время для непосредственного изучения. Вот почему в таких случаях прибегают к использованию неполной индукции, которая на практике применяется значительно шире, чем полная.

Неполная индукция - это умозаключение, в котором на основе повторяемости признака у некоторых явлений определенного класса делается вывод о принадлежности этого признака всему классу явлений. Неполная индукция имеет следующую схему рассуждений:

S 1 - Р

S 2 - Р

S 3 - Р

S 1 , S 2 , S 3 , ... составляют класс К

Вероятно, каждый элемент К - Р

Неполная индукция часто применяется в реальной жизни, так как позволяет делать заключение на основе анализа определенной части данного класса предметов, экономит время и силы человека. Правда, в этом случае мы получим вероятностное заключение, которое в зависимости от вида неполной индукции будет колебаться от менее вероятного к более вероятному. Например :

Слово "молоко" изменяется по падежам

Слово "библиотека" изменяется по падежам

Слово "врач" изменяется по падежам

Слово "чернила" изменяется по падежам

Слова "молоко", "библиотека", "врач", "чернила" - существительные

−Вероятно, все имена существительные изменяются по падежам

По способам обоснования заключения различают следующие виды неполной индукции: популярную и научную.

В популярной индукции на основе повторяемости одного и того же признака у некоторой части однородных предметов и при отсутствии противоречащего случая делается общее заключение, что все предметы этого рода обладают этим признаком. Степень вероятности заключения в популярной индукции невысока, так как неизвестно, почему дело обстоит так, а не иначе.

Выводы популярной индукции - часто начальный этап формирования гипотезы. Главная ценность данного вида умозаключения состоит в том, что оно является одним из эффективных средств здравого смысла и дает ответы во многих жизненных ситуациях, причем нередко там, где наука безмолвствует. На основе популярной индукции народ вывел немало примет, пословиц и поговорок. Например: "Когда туман, с неба вниз опускаясь, ложится на землю, значит к доброй погоде, а ежели с вечера туман от земли или воды поднимается, на утро - жаркий день".

Эффективность популярной индукции во многом зависит от того, насколько число случаев, закрепленных в посылках, по возможности будет: а) больше, б) разнообразнее, в) типичнее.

Вероятность заключения популярной индукции значительно увеличится, если мы в рассуждениях не будем допускать следующие логические ошибки.

1. Поспешное обобщение.

2. "После этого, значит, по причине этого". Кроме того, данная ошибка лежит в основе многих суеверий и предрассудков.

3. Подмена условного безусловным.