Фигуры и правила фигур простого категорического силлогизма.

В посылках простого категорического силлогизма средний термин может занимать место субъекта или место предиката. В зависимости от этого различают четыре разновидности силлогизма, которые называются фигурами. Различное положение среднего термина в разных фигурах хорошо видно при их сравнительном графическом изображении. Средний термин занимает разные места в посылках и отсутствует в заключении:

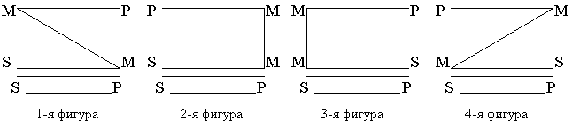
В первой фигуре средний термин М замещает субъект S в большей посылке и предикат Р в меньшей:

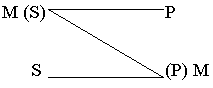
Во второй фигуре средний термин М замещает предикат Р в обеих посылках:

В третьей фигуре средний термин М занимает место субъекта S в обеих посылках:

В четвертой фигуре средний термин М замещает предикат Р в большей посылке и субъект S в меньшей:

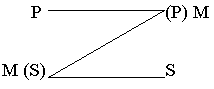
Теперь дадим определение фигур:

Фигуры силлогизма - это его разновидности, различающиеся положением среднего термина в посылках. Четыре фигуры исчерпывают возможные комбинации терминов.

Дальнейшее разнообразие силлогизмов образуется за счет посылок. По определению силлогизма, его посылки – категорические суждения. Последние бывают четырех видов: А-общеутвердительные, Е-общеотрицательные, I-частноутвердительные, О-частноотрицательные. Каждое из суждений A, E, I, O может быть посылкой силлогизма. Разместим их по вертикали.
Например:

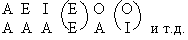
Поскольку посылок две, то каждая из них может принимать вид одного из четырех суждений A, E, I, O. В таком случае, число возможных комбинаций для каждой фигуры будет равно 2⁴ = 16, а число возможных комбинаций для 4-х фигур = 64 (16 x 4).

Образование модусов простого силлогизма и проверка их правильности.

Разновидности силлогизма, различающиеся качеством и количеством посылок, называются модусами силлогизма. Не все из 64-х силлогизмов являются правильными, т.е. удовлетворяют общим правилам силлогизма. Например, заключенные в скобки сочетания посылок противоречат 3-му и 1- му правилам силлогизма. На самом деле из 64-х модусов силлогизма только 19 являются правильными. Заключения этих силлогизмов всегда истинны. Эти модусы принято распределять по фигурам и записывать с заключением. Кроме того, существует латинский вариант их названий, который является мнемоническим приемом, т.е. облегчает их запоминание, а также содержит шифр сведения 2-й, 3-й и 4-й фигур силлогизма к 1-й, которая со времен Аристотеля и по наши дни считается совершенной, т.к. позволяет в качестве заключения получать все четыре вида суждений: А, Е, I, О. В каждом латинском названии правильного модуса есть только три гласных. Каждая гласная обозначает определенный тип суждения. Первые две указывают на посылки, а третья – на заключение силлогизма. Например, модус Barbara состоит из суждений А А → А. Согласные латинские буквы указывают на алгоритм сведения модусов трех вышеуказанных фигур к модусам первой.