Относительное количество ложных тревог

Рис. 5. РХП для трех сигналов различной распознаваемости: на абсциссе — относительное количество ложных тревог, на ординате — относительное количество попаданий. Каждая кривая соответствует определенному уровню чувствительности к восприятию сигнала данной интенсивности. (Величина d' — количественное выражение чувствитель­ности наблюдателя, описанной в тексте)

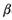
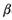терия но если их соответствующим образом обработать, они лягут на кривую рис. 4. Следовательно, конкретная РХП отражает способность наблюдателя обнаруживать сигнал определенной интенсивности, а это значит, что чувствительность наблюдателя постоянна во всех ее точках. Интенсивность сигнала и способность наблюдателя обнаруживать его не изменяются. А вот что действительно изменяется вследствие изменения уровня критерия наблюдателя , так это соотношение попаданий и лож­ных тревог.

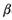
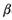Мы старались привлечь внимание читателя к тому, что точки на кривой рис. 4 соответствуют сигналу постоянной интенсивности. Когда интенсивность сигнала увеличивается, его обнаружение облегчается; бо­лее интенсивному сигналу соответствует другая кривая. То же самое может быть сказано и о более слабом сигнале — ему тоже соответствует своя кривая. (Примеры разных РХП представлены на рис. 5.) Следова­тельно, РХП показывает, как изменение уровня критерия наблюдателя (в данном случае — под влиянием изменения ожидания сигнала) влияет на соотношение попаданий и ложных тревог при постоянной интенсив­ности сигнала. Каждая РХП иллюстрирует влияние d' — чувствительно­сти наблюдателя к сигналу постоянной интенсивности — плюс влияние уровня его критерия

Шиффман X. Теория обнаружения сигнала (ТОС)

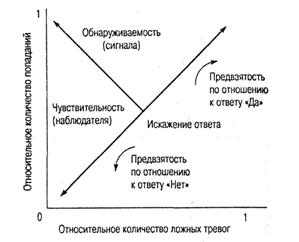Рис. 6. Принципиальные особенности РХП Лежащая под углом 45° диагональ искажения ответа соответствует случайному поведению наблюдателя, при котором количество попада­ний равно количеству ложных тревог

Чувствительность: величина d’ На рис. 6 для наглядности пред­ставлены основные принципиальные особенности РХП, показывающие, как ее кривизна отражает чувствительность наблюдателя к сигналу и искажение его ответа, или влияние критерия (см. рис. 5). Выше уже отмечалось, что при увеличении интенсивности сигнал становится более распознаваемым и увеличивается наклон кривой влево. Чем слабее сиг­нал, тем ближе кривая к диагонали, лежащей под углом 45°. (Диагональ соответствует случайному поведению испытуемого, при котором ко­личество попаданий и ложных тревог одинаково.) Иными словами, откло­нение РХП влево от диагонали зависит исключительно от интенсивнос­ти сигнала и не зависит от искажения ответов испытуемого.

Степень наклона, или кривизна РХП, может быть рассчитана из соотношения попаданий и ложных тревог и является мерой чувствитель­ности наблюдателя к сигналу определенной интенсивности (d'). На прак­тике величину d' определяют как линейное расстояние данной РХП от диагонали. На рис. 5 приведены РХП для значений d', изменяющихся от 0 до 3. Чем выше d' (и чем более изогнута кривая), тем выше коли­чество попаданий и тем меньше количество ложных тревог. Следователь­но, чем выше значение d', тем более чувствителен наблюдатель к дейст­вию сигнала данной интенсивности и тем более распознаваем сам сигнал. Если пользоваться графическими терминами, то степень искрив-

Тема 17. Экспериментальные исследования восприятия

Низкий Средний Высокий

Уровень сенсорной активности

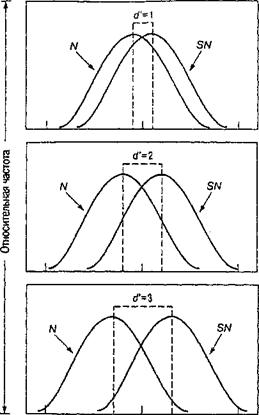
Рис. 7. Кривые распределения Ш и СШ для трех РХП, представленных на рис. 6 Значение d' изменяется в зависимости от смещения распределе­ния СШ относительно распределения Ш и равно расстоянию меж­ду средними значениями Ш и СШ. Для d’'=0 кривые распределе­ния СШ и Ш полностью совпадают. Следовательно, величина d' характеризует интенсивность сигнала и чувствительность к нему наблюдателя, не зависящую от искажения ответа

ления РХП является мерой чувствительности испытуемого к сигналу, имеющему постоянную интенсивность. Разные значения (d' разных лю­дей (при условии, что речь идет о сигнале постоянной интенсивности) отражают их разную чувствительность к данному сигналу.

Описание способа расчета d' выходит за рамки данной книги. Од­нако важно понимать, что d' является мерой чувствительности наблюда-

Шиффман X. Теория обнаружения сигнала (ТОС)

теля к интенсивности сигнала, не зависящей от его критерия или ис­кажения ответа. Для наглядности эта мысль может быть проиллюстри­рована графическим изображением сенсорных эффектов, на основании которых построены РХП, представленные на рис. 5. Обратите внимание на то, что d' представляет собой линейное расстояние между двумя сен­сорными распределениями, о которых шла речь в начале обсуждения ТОС, а именно распределений Ш и СШ (см. рис. 7). По мере увеличения интенсивности сигнала кривая распределения СШ смещается вправо от кривой распределения Ш. Напротив, если интенсивность сигнала мала, кривые распределений Ш и СШ располагаются очень близко друг к дру­гу. Так, если d' — 1, кривые распределений Ш и СШ сравнительно близ­ко примыкают друг к другу; сигнал относительно слаб, и поэтому его обнаружение затруднено. (Случайно оказалось, что для данных табл. 5, использованных при построении рис. 4, d' = 1). Напротив, при d '= 3 сиг­нал сравнительно интенсивен и его влияние на сенсорную систему весь­ма легко отделить от влияния шума. Следовательно, при увеличении интенсивности сигнала распределение СШ смещается еще дальше от рас­пределения Ш, что приводит к увеличению значения d'. Иными слова­ми, высокая величина ^'свидетельствует о том, что сигнал интенсивен и/ или что наблюдатель чувствителен к данному конкретному сигналу. А это значит, что d' является мерой чувствительности к сигналу, не зависящей от таких несенсорных факторов, как ожидания наблюдателя и другие подходы к принятию решений. Подводя некоторый итог, можно сказать: d' отражает возможность обнаружить сигнал данной интенсивности, что определяется исключительно чувствительностью наблюдателя.

Насколько релевантна эта информация? Мы начали с проблемы определения абсолютного порога, но для этого мы познакомились с пси­хофизическим методом, который представляется весьма сложным и гро­моздким. Относительно обнаружения слабых сигналов в ТОС прежде все­го отмечается, что даже простые, вполне заурядные эксперименты, такие как решение вопроса о наличии сигнала, вовсе не так точны, как мы думаем. Более того, ТОС позволяет исследователю делать то, чего не по­зволяет традиционный подход к порогам: оценивать влияние несенсор­ных искажающих факторов (критерия ) на принятие решений наблюда­телем в ходе эксперимента по обнаружению сигнала. Как мы видели, решение наблюдателя о наличии или отсутствии сигнала зависит от его предыдущего опыта, который он привносит в выполнение задания, а так­же от его ожиданий, мотивации, внимания и, возможно, от других не­сенсорных психологических факторов. Может быть, самой сильной сто­роной ТОС является то, что она позволяет нам отделить сенсорную спо­собность наблюдателя, имеющего дело с пограничным сигналом, от несенсорных искажений его ответа и оценить ее.

Все сказанное выше свидетельствует о том, что не существует одного-единственного, абсолютного стимула с минимальной обнаруживав-

Тема 17. Экспериментальные исследования восприятия

мой — пороговой — величиной. Однако это вовсе не значит, что само понятие порога ощущений должно быть отброшено за ненадобностью. Более правильным будет признание того факта, что общее понятие поро­га включает в себя и описывает отношение величин, восприятие которых зависит от различных несенсорных внешних факторов и индивидуальных особенностей наблюдателя. На самом деле порог как статистическое сред­нее — очень полезное понятие, имеющее чрезвычайно широкое приме­нение. Он делает возможным важную аппроксимацию энергетического интервала и пределов сенсорной системы. Мы считаем, что необходим осторожный подход к интерпретации данных, характеризующих порог; они скорее представляют собой статистические приближения, дающие представление о средней величине и/или об интервале значений, нежели точные энергетические величины.

4. Фурье-анализ зрительного восприятия

А.Д. Логвиненко [ПОНЯТИЕ СЕНСОРНОГО ОПЕРАТОРА]¹

Психофизическая связь между чувственной тканью образа и прок­симальным стимулом составляет предмет нашего исследования. Выбор предмета исследования предопределил как выбор метода исследования, так и сферу приложимости полученных нами результатов.

В дальнейшем ограничимся случаем, когда дистальные стимулы являются двумерными черно-белыми изображениями. Положим для оп­ределенности, что эти плоские изображения всегда располагаются во фронтальной плоскости. Будем называть эту плоскость стимульной плос­костью. Глаз человека устроен таким образом, что в плоскости сетчатки формируется новое изображение, которое мы будем называть проксималь­ным изображением. Проксимальное изображение — это та реальность, с которой имеет дело зрительная система. Хорошо известно, что нервным субстратом высших форм зрительного восприятия являются зрительные отделы (17, 18 и 19 поля по Бродману) коры больших полушарий голов­ного мозга. Известно также, что при передаче нервного возбуждения от сетчатки в зрительные отделы коры соблюдается принцип топической проекции. Это дает основание отнестись к процессу передачи нервного возбуждения в зрительной системе как к процессу передачи изображения.

С другой стороны, чувственную ткань зрительного образа можно так­же рассматривать как своеобразное изображение. Действительно, если аб­страгироваться от предметного содержания образа, то он предстает в виде распределения светлоты в субъективном двумерном пространстве и субъек­тивном времени. В результате мы имеем следующую цепочку: дистальное изображение — проксимальное изображение — чувственная ткань образа (как субъективное изображение). Возникает возможность отнестись к зре­нию как к последовательности преобразований одного изображения в дру­гое. Привлекательность этого подхода в немалой степени связана с суще-

¹ Фурье-анализ зрительного восприятия / Под ред. А.Д. Логвиненко. М.: Изд-во Моск. ун-та, 1982. С. 6-8.

Тема 17. Экспериментальные исследования восприятия

ствованием мощного аппарата для анализа физических систем, преобразу­ющих изображения. Разумеется, обращение к этому довольно сложному математическому аппарату будет оправданным лишь в том случае, если с его помощью удастся объяснить немного больше, чем мы это умеем делать и без него. <...>

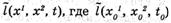Анализ преобразования изображений невозможен без решения одной проблемы, которая связана со способом представления изображений. Выбор способа представления изображения не является совершенно произвольным и во многом определяется выбором математического аппарата для анализа преобразования изображений. Наиболее употребительный способ представ­ления изображений состоит в описании изображения посредством неотри­цательной функции пространственных и временной переменных l (x¹, x², t). Смысл этой функции в том, что она описывает распределение интенсивнос­ти в плоскости изображения. Таким образом, в момент t₀ в точке с коорди­натами (х₀¹, x₀²) пространственно-временная плотность световой энергии рав­на 1(х₀¹, х₀², t₀). Точно так же чувственную ткань зрительного образа будем описывать неотрицательной функцией — светло­та (субъективная интенсивность или как еще иначе говорят, видимая яр­кость) в точке с координатами (x₀¹, х₀²) в момент времени t_Q.

Возникает вопрос: насколько операционализируемо такое представ­ление чувственной ткани зрительного образа (поскольку в дальнейшем мы будем иметь дело лишь с чувственной тканью зрительного образа, то ради краткости будем говорить просто образ, подразумевая всюду при этом его чувственную ткань). Методы измерения субъективных величин, разработанные в психометрике¹, предоставляют возможность измерять светлоту точечного источника света. Следовательно, мы в принципе мо­жем построить функцию светлоты, так сказать, поточечно, как это дела­ют школьники, строя график функции «по точкам». Разумеется, такая процедура неимоверно трудоемка и насколько нам известно, для реаль­ных двумерных изображений эту процедуру в полном объеме никто не проводил. Впрочем, в этом и нет большой нужды, как это будет ясно из дальнейшего изложения.

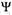Итак, постановка центральной для настоящего изложения пробле­мы состоит в том, чтобы отыскать такое преобразование, которое дистальное изображение переводит в образ. На математическом языке это озна­чает, что проблема состоит в отыскании оператора, отображающего мно­жество яркостных функций, представляющих дистальное изображение L — {1(х¹, х², t)} в множество функций светлоты, представляющих образ L= {l(x¹, х², t)}. Этот гипотетический оператор мы в дальнейшем будем называть сенсорным оператором :

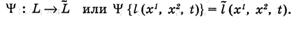¹ См.: Guilford J.P. Psychometric Methods. N. Y. : Mc Graw Hill, 1954.

X. Шиффман АНАЛИЗ ПРОСТРАНСТВЕННОЙ ЧАСТОТЫ¹

Если внимательно осмотреть то, что в данный момент находится у нас перед глазами, не обращая внимания на цвета, то даже поверхност­ный анализ позволит сказать, что мы видим чередование светлых и тем­ных участков. Любую сложную визуальную картину можно представить в виде мозаики, или матрицы, светлых и темных зон. При составлении таких матриц наиболее релевантными считаются два компонента: число контрастных светлых и темных участков (или их частота) и степень контраста между соседними светлыми и темными участками. Каким бы искусственным и механистическим ни казался этот анализ, указанные компоненты визуального паттерна достаточно информативны и могут оха­рактеризовать любую сложную картину; они с успехом использовались для описания базовых единиц, используемых зрительной системой для кодирования визуальной информации об окружающем мире. (Однако, как будет показано ниже, психологами найдено и идентифицировано много других компонентов физических раздражителей, которые также исполь­зуются для этой цели.)

Пространственные частоты

Любой участок поля зрения, образованный контрастными светлы­ми и темными участками, можно проанализировать и трансформировать в его пространственную частоту — в число вариаций светимости на определенном участке пространства. Для большей наглядности простран­ственную частоту можно определить как число циклов чередования тем­ных и светлых полос на данном участке поля зрения. Чем больше полос приходится на единицу площади паттерна, тем выше его простран-

¹ Шиффман X. Ощущение и восприятие. СПб.: Питер, 2003. С. 243-253.

Тема 17. Экспериментальные исследования восприятия

Рис. 1, Типы решеток, под каждым из них представлен соответствующий ему профиль светимости:

А — решетка синусоидального типа; Б — синусоидальная решетка с той же частотой, что и А, но менее контрастная; В — решетка квадратурно-волнового типа; Г — синтез квадратурной волны с помощью синтеза Фурье. Сложение компонентов Фурье приводит к аппроксимации квадратурной волны (f пред­ставляет собой частоту исходной синусоиды, соответствующей одному циклу)

Шиффман X. Анализ пространственной частоты

ственная частота. Следовательно, паттерны с высокими пространствен­ными частотами состоят из мелких деталей, паттерны с низкими про­странственными частотами — из крупных элементов. На практике про­странственной частотой называют число циклов изменения светимости на один градус угла зрения (циклов/градус). Подобное определение свя­зывает единицы измерения пространственной частоты со специфической единицей измерения величины образа на сетчатке — углом зрения <...> и устраняет необходимость специально оговаривать связь между величи­ной конкретных контрастных участков и расстоянием, с которого они воспринимаются.

Решетчатые паттерны и контраст. Решетчатыми паттернами на­зываются паттерны, состоящие из примыкающих друг к другу светлых и темных полос. Они используются в качестве «строительных блоков» при создании сложных зрительных композиций, и в этом заключается их практическая ценность, Примеры типичных решетчатых узоров представ­лены на рис. 1, А, Б, В. Под каждым узором приведены соответствую­щие им распределения интенсивности света, называемые профилями све­тимости. Обратите внимание на то, что полосы решеток, представлен­ных на рис. 1, А и Б, не имеют четких, хорошо очерченных краев, их заменяет постепенный переход от светлых участков к темным. В соответ­ствии с этим профили светимости этих паттернов представляют собой си­нусоиды, а подобные решетки называются синусоидальными, или сину­соидально-волновыми (sine-wave) решетками. Известны также и паттер­ны, профили светимости которых больше похожи на изломанные прямые, чем на кривые. На рис. 1, В представлен такой паттерн, называемый квадратурно-волновой решеткой. Квадратурно-волновый профиль свети­мости соответствует серии регулярно повторяющихся темных и светлых полос с четкими краями.

Кривая распределения интенсивности, представленная профилем светимости паттерна решетки (под каждым паттерном приводится его про­филь светимости), отражает степень контраста, характерную для всего пат­терна. Обратите внимание на то, что все узоры, представленные на рис. 1, имеют одинаковое количество циклов, или одинаковую пространственную частоту, но отличаются друг от друга распределением интенсивности, или контраста. Слово «контраст» в данном контексте употребляется для обо­значения разницы в светимости темных и светлых полос. Чем больше раз­ница, тем больше и контраст.

Ряд Фурье. Каким образом сложная зрительная картина связана с паттернами синусоидальных решеток, о которых мы только что рас­сказали? Прежде всего вспомните, что визуальный образ представляет собой паттерн освещенностей, т.е. он представляет собой сумму ряда простых компонентов. Используя специальный математический прием, называемый анализом Фурье, можно трансформировать сложное про­странственное распределение освещенности всей зрительной картины в

98 Тема 17. Экспериментальные исследования восприятия

синусоидальные волны ее простых компонентов, называемые компонен­тами Фурье, Этот прием основан на теореме Фурье, математическом принципе, сформулированном в начале XIX в, французским физиком и математиком Жаном Батистом Фурье (1768—1830). Коротко ее суть можно сформулировать следующим образом: любой сложный паттерн, состоящий из простых повторяющихся элементов, может быть представ­лен рядом простых синусоидальных волн. Как сказано выше, ряд Фурье позволяет проанализировать любой паттерн, или зрительный образ, не­зависимо от степени сложности как совокупность синусоидальных волн его/ее компонентов.

Точно так же возможно и обратное действие — суммирование си­нусоидальных волн компонентов для получения сложного паттерна. Этот рекомбинационный процесс называется синтезом Фурье. Пример синте­за Фурье, представленный на рис. 1, Г, показывает, как следует объе­динить синусоидальные волны f, 3f, 5f и 7f, чтобы образовался паттерн, распределение интенсивностей, или профиль светимости, которого при­ближается к квадратурной волне f + 3f + 5f + 7f. Обратите внимание на то, что сходство этого распределения с распределением, представленным на рис. 1, В, возрастает по мере того, как надлежащим образом прибав­ляются более высокие частоты (например, 9f, 11f, 13f).

Детекторы пространственной частоты. Предположим, что зритель­ная система выполняет анализ пространственной частоты сложного объекта. Скорее всего, этот объект, разложенный и проанализированный так, как описано выше, будет содержать участки с высокой и с низкой пространственной частотой и с высокой и низкой контрастностью. Чет­ко просматриваемым, текетурированным участкам зрительного образа будут соответствовать высокие пространственные частоты (с многочис­ленными изменениями светимости), а участкам, содержащим более гру­бые, крупные и менее детализированные элементы, — низкие простран­ственные частоты (с немногочисленными изменениями светимости). Как мы скоро узнаем, есть доказательства существования в зрительной сис­теме детекторов пространственной частоты — специализированных кле­ток, или каналов, «настроенных» на определенные изменения светимос­ти. Иными словами, в зрительной системе есть некие нейронные едини­цы, максимально чувствительные к определенным пространственным частотам. Следовательно, исходя из данных об анализе пространственной частоты можно сказать, что наше восприятие любого сложного визуаль­ного образа является результатом анализа и синтеза зрительной систе­мой образующих его пространственных частот. А это значит, что мозг реконструирует зрительный образ объекта, интегрируя информацию о разных пространственных частотах, получаемую по разным каналам, стимулируемым его компонентами.

Шиффман X. Анализ пространственной частоты

Функция контрастной чувствительности

Как отмечалось выше, характерными особенностями любого паттер­на являются его пространственная частота (т.е. число вариаций интен­сивности или светимости) и контраст (различие в интенсивностях между элементами паттерна). Существует определенная связь между простран­ственной частотой и контрастом: при одном и том же контрасте некото­рые пространственные частоты воспринимаются более четко, нежели дру­гие. То, что одни пространственные частоты можно отличить от других при меньшем контрасте, свидетельствует о разной чувствительности ви­зуальной системы к разным пространственным частотам. Это становится очевидным при рассмотрении паттернов пространственной частоты, име­ющих разную светимость (рис. 2).

На экране представлен неоднородный паттерн синусоидальных ре­шеток, пространственная частота которых возрастает слева направо, а контраст — сверху вниз. Чтобы различить частоты, расположенные в правой части экрана, нужна большая контрастность, чем для того, что­бы различить частоты в левой части, т.е. порог восприятия этих частот

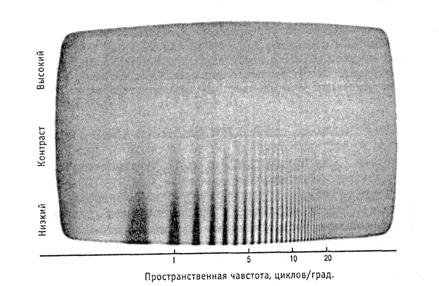Рис. 2. Паттерн, содержащий синусоидальные решетки, прост­ранственная частота которых увеличивается слева направо, а конт­раст — сверху вниз. Большинство людей лучше всего видят простран­ственные частоты в центре. Из-за недостатков полиграфии этот рису­нок, на котором плохо видны или вовсе отсутствуют некоторые дета­ли паттерна, может служить лишь приблизительной иллюстрацией

Тема 17. Экспериментальные исследования восприятия

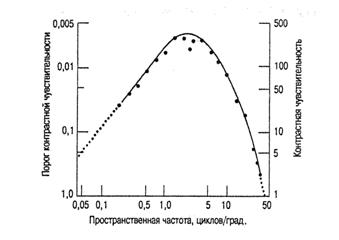Рис. 3. Функция контрастной чувствительности Кривая отражает связь порога светового контраста и чувствительности зри­тельной системы к разным воспринимаемым ею пространственным часто­там. На левой ординате отложены значения порогов восприятия контрас­та, соответствующие различению каждой частоты, на правой — значения, обратные световым порогам. Средние пространственные частоты видны при меньшем световом контрасте, чем низкие или высокие. Следовательно, зрительная система обладает наибольшей чувствительностью к средним пространственным частотам, равным примерно 3 цикла/градус (вывод сде­лан на основании определенного изученного интервала частот)¹

выше, а чувствительность зрительной системы к ним — ниже. Иными словами, чем меньший контраст нужен для того, чтобы простран­ственные частоты были видимыми, тем выше чувствительность зритель­ной системы к этим частотам.

Рассмотрим зависимость пороговых уровней контраста и простран­ственной частоты, характеризующую чувствительность зрительной систе­мы к тому интервалу пространственных частот, для которого определена эта зависимость. Связь между пространственной частотой и пороговыми уровнями контраста называется функцией контрастной чувствительнос­ти. Зависимость контрастной чувствительности от пространственной час­тоты, определенная по данным рис. 2, представлена на рис. 3 в виде функ­ции контрастной чувствительности.

Для паттернов с низкими пространственными частотами (т.е. обра­зованных крупными или лишенными деталей участками) порог контраст-

¹ См.: Howard LP. Human visual orientation. N. Y.: Wiley, 1982.

Шиффман X. Анализ пространственной частоты

ной чувствительности высок (левая ордината) и чувствительность отно­сительно низка (правая ордината). Это значит, что для различения пат­терна нужен большой контраст. По мере увеличения пространственной частоты (продвижение по экрану рис. 2 слева направо) световой порог, необходимый для различения паттерна, понижается и повышается чув­ствительность. Однако для паттернов с очень высокими простран­ственными частотами (они приблизительно представлены в правой части экрана рис. 2) величины световых порогов возрастают и чувствительность понижается.

На рис. 3 представлена зависимость физического контраста, необ­ходимого для различения решетки, от пространственной частоты визу­ального паттерна (или от изменений его интенсивности). Из этого рисун­ка следует, что число изменений интенсивности — для превращения паттерна решетки в видимый — должно соответствовать пространствен­ной частоте, и эти изменения проявляются наиболее отчетливо в тех слу­чаях, когда они происходят при средних значениях пространственных частот (максимальное число изменений интенсивности соответствует про­странственной частоте, равной 3 цикла/град., что согласуется с данны­ми рис. 2). Когда перемены в интенсивности происходят слишком часто (т.е. когда пространственная частота очень велика) или слишком редко (т.е. когда пространственная частота слишком мала), чувствительность к изменениям понижается. Следовательно, зрительная система менее чувствительна к очень низким и очень высоким пространственным час­тотам, чем к средним.

Одна из причин повышенного интереса к пространственной часто­те связана с тем, что, как уже отмечалось нами, любой визуальный об­раз может быть представлен сложным набором паттернов, каждый из которых имеет свою собственную пространственную частоту. Неструкту­рированные участки визуального образа имеют низкую пространствен­ную частоту, а элементы и участки, содержащие мелкие детали, — высокую. Следовательно, можно сказать, что, в известном смысле, на определенном уровне зрительной системы выполняется Фурье-преобра­зование пространственных частот, содержащихся в визуальном стимуле, т.е. определяются компоненты Фурье его паттерна. Если такой анализ будет выполнен, визуальная система получит информацию об индиви­дуальных синусоидальных компонентах (о компонентах Фурье) сложно­го паттерна. Иными словами, в зрительной системе могут быть дискрет­ные, независимые нейроны (или каналы), каждый из которых «настро­ен» на определенный, но ограниченный интервал пространственных частот, чувствительность к которому у него максимальна. Один из спо­собов доказательства независимости каналов, обрабатывающих информа­цию о пространственной частоте, включает использование селективной адаптации.

Тема 17. Экспериментальные исследования восприятия

Селективная адаптация

Наличие в зрительной системе специализированных каналов, вос­принимающих пространственную частоту, может быть доказано методом, основанным на селективной адаптации, понятие о которой было введе­но <..,> при обсуждении феномена последействий. Метод селективной адаптации основан на том, что наблюдатель сосредоточивает свое внима­ние на определенных характеристических признаках какого-либо объек­та (например, на его цвете, форме или присущей данному объекту спе­цифической пространственной частоте). Считается, что пристальное «всматривание» в подобные признаки «утомляет» нейроны или нейрон­ные структуры, стимулируемые ими. На восприятии это сказывается таким образом, что чувствительность к определенному, пристально рас­сматриваемому признаку предмета уменьшается. Ниже приводится опи­сание эксперимента, доказывающего факт существования селективной адаптации к пространственной частоте.

Можно предположить, что наблюдаемое явление — следствие влия­ния селективной адаптации. Предварительная фиксация взгляда на решетках (рис. 4, А) «утомила» каналы, настроенные преимущественно на восприятие низких пространственных частот (верхний паттерн на рис. 4, А). Это повлияло на восприятие средней пространственной частоты вер­хнего паттерна (рис. 4, В) таким образом, что она стала казаться выше пространственной частоты «адаптационной» решетки на рис. 4, А. Ана­логичным образом адаптация, или усталость, каналов, наиболее чувст­вительных к высоким пространственным частотам (нижний паттерн на рис. 4, А), приводит к тому, что средняя пространственная частота ниж­ней решетки на рис. 4, Б кажется ниже, чем пространственная частота той решетки, которую вы пристально рассматривали, — решетки на рис. 4, А. Следовательно, если каналы зрительной системы адаптируют­ся (и вследствие этого становятся менее чувствительными) к паттерну с определенной пространственной частотой, восприятие решеток с анало­гичными пространственными частотами изменяется именно так, как и следовало ожидать на основании допущения о существовании каналов, специализирующихся на восприятии пространственной частоты, а имен­но в направлении, противоположном пространственной частоте решетки, вызвавшей селективную адаптацию.

Экспериментальное подтверждение