Определение дедуктивного следования для ЛВ и метод проверки логичности умозаключений ЛВ

С рассмотрением логичных умозаключений, как нетрудно понять, завершается построение элементарного курса базисной части общей практической логики. Понятно, что для построения практической части ЛВ необходимо дать адекватное для ЛВ определение дедуктивного логического следования. Поскольку с обычной точки зрения логичность рассуждения (умозаключения) понимается как рассуждение в соответствии с определённым законом логики, постольку для практической части ЛВ представляется адекватным определение дедуктивного следования в метаязыке ЛВ через понятие закона ЛВ в следующем виде: из высказываний А⁰₁, А⁰₂, …, А⁰_n, 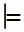(дедуктивно следует) высказывание В⁰ в некотором умозаключении ЛВ, если и только если импликация вида (А₁ А₂ …, А_n) B есть закон ЛВ[34]. Очевидно, что в этом определении выражение А₁ А₂ …, А_n представляет конъюнкцию посылок, выражение В – заключение умозаключения, а вся импликация в целом имеет прочтение «если А₁ А₂ …, А_n, то В», т. е. черта в умозаключении прочитывается как импликация «если… то…»

Данное определение задает следующий стандартный метод проверки дедуктивности (логичности, правильности) умозаключения ЛВ, состоящий из следующих шагов:

1) сначала умозаключение приводится к каноническому виду и выявляется его логическая форма в виде формул-посылок и формулы - заключения;

2) затем формулы-посылки соединяются знаком « » (конъюнкция), и полученная сложная формула соединяется знаком « » (импликация) с формулой - заключением, образуя в итоге сложную формулу с главным знаком « » (импликация);

3) для полученной импликативной формулы строится таблица истинности, и если обнаружится, что: а) во всех строках выходного столбца таблицы истинности стоит только значение «и» («истина»), то это значит, что данная формула является тождественно-истинной (общезначимой), т. е. является законом ЛВ, что позволяет на основе сформулированного выше определения дедуктивного следования для умозаключений ЛВ признать, что анализируемое умозаключение является дедуктивным и, следовательно, правильным, а также логичным. При этом таблица истинности покажет, что в ней нет такой строки («возможного мира» по терминологии Л. Витгенштейна), чтобы конъюнкция формул-посылок была истинной, а формула-заключение оказалась ложной, что полностью согласуется с интуитивным пониманием логичности умозаключения.

Если же обнаружится, что: в) в выходном столбце таблицы истинности формулы - импликации имеется значение «и» («истина) и значение «л» (ложь), т.е. вся формула является нейтральной и в ней найдется горизонтальная строка, в которой сложная формула, представляющая конъюнкцию формул-посылок, – истинна, и формула, представляющая заключение, также истинна, то данное умозаключение следует отнести к числу правдоподобных и, следовательно, правильных, а также логичных.

И лишь в случае с), если обнаружится, что во всех строках выходного столбца таблицы истинности формулы - импликации стоит только значение «л» (ложь), т. е. обнаружится, что формула является тождественно-ложной, то анализируемое заключение следует отнести к числу недедуктивных и неправдоподобных, и, следовательно, его нужно квалифицировать как неправильное и нелогичное, так как в нем посылки и заключение находятся в отношении противоречия.

Ниже мы рассмотрим лишь наиболее употребительные дедуктивные и правдоподобные умозаключения ЛВ.