Общая характеристика понятия. Понятия и имена
Определение понятия: понятие есть мысль, в которой на основе фиксирования определённых признаков в сознании человека обобщаются предметы из некоторого исходного множества и выделяются в определённый класс[19]. При этом исходное множество предметов рассматривается как универсум рассуждения и обозначается U.
Примеры понятий:
(1)Общественно опасное деяние, предусмотренное Уголовным кодексом (преступление);
(2)Тайное хищение имущества или денег (кража);
(3)Часть суши, окружённая со всех сторон водой (остров);
(4)Четырехугольник, у которого все стороны равны и все углы прямые (квадрат);
(5)Слово, обозначающее предмет и отвечающее на вопросы «кто?» или «что?» (имя существительное);
(6)Столица Российской Федерации (Москва);
(7)Плоская геометрическая фигура, имеющая вид круга и квадрата (круглый квадрат).
Поясним дефиницию понятия на данных примерах.
Для первого примера. Если мы в своём сознании промысливаем (фиксируем) признак быть деянием, то это значит, что мы отвлеклись от некоторых признаков, которыми обладают отдельные деяния из множества деяний, совершаемых людьми. Эти деяния могут совершаться днём либо ночью, отдельными людьми либо группой людей, мужчинами либо женщинами, с умыслом либо без умысла и т.д. Но отвлекаясь от этих признаков и мысленно удерживая в сознании признаки быть общественно опасным и быть предусмотренным Уголовным кодексом, мы тем самым сделали обобщение отдельно взятых конкретных деяний и выделили их в отдельный класс деяний, называемых преступлениями, который является правильным подмножеством исходного множества деяний.
Аналогичный результат мы получим при анализе других понятий, перечисленных в списке примеров понятий.
На основе примеров (1) – (7) мы можем заключить, что понятие как форма мышления имеет направленность от мышления существующего общего к мышлению существующего особенного (см. примеры понятий (1) – (5); от мышления существующего общего к мышлению существующего единичного (см. пример понятия (6) и в пределе от мышления существующего общего к мышлению несуществующего (см. пример понятия (7).
Для более ясного понимания определения понятия разъясним смысл слов «предмет», «признак», «множество», «класс», которые входят в определение понятия.
Предмет в логике понимается широко. Предметы в логике – это и отдельные физические вещи, и их множества, и отдельные метафизические сущности, и их множества. В пределе предметы в логике – это всё то, что можно помыслить. А помыслить можно и противоречиво мыслимые сущности, такие, как «некруглый круг», «круглый квадрат», а также непротиворечиво мыслимые, но реально не существующие сущности, такие, как «вечный двигатель», «крылатая лошадь» и т. д. Хотя для обеспечения логичной корректности рассуждений (умозаключений) следует избегать включения в рассуждение (умозаключение) пустых терминов, т.е. терминов, не имеющих в качестве предметного значения физический либо метафизический объект.
Так же широко в логике понимают признаки. При самом общем подходе под признаками в логике понимают всё то, в чём предметы сходны друг с другом и чем они отличаются друг от друга. Дальнейшая конкретизация понимания признака наводит на мысль, что сходство и отличие предметов обеспечивается наличием либо отсутствием у них определенных свойств или отношений. В итоге под признаком предмета в логике понимают наличие или отсутствие у предмета определённых свойств или отношений. В соответствии с этим все признаки можно разделить на признаки - свойства и признаки - отношения. При этом под свойствами понимают характеристики, присущие отдельно взятым предметам. В русском языке признаки - свойства выражаются прилагательными (белый, красный, твёрдый, мягкий, высокий, низкий и т. д.), а также существительными вместе со словом «есть» (есть человек, есть планета, есть жидкость, есть предмет и т.д.).
Соответственно под отношениями в логике понимают характеристики, присущие (одновременно) парам, тройкам и в общем случае n-кам предметов, где n ≥ 2. Примеры слов русского языка, выражающие отношения: «больше», «меньше», «равно», «делиться на», «брат», «родственник», «причина», «столица», «расположен между… и …» и т. д.
В общей практической логике наиболее употребительны двухместные и трёхместные отношения.
Местность отношения определяется числом различных предметов, которые связываются отношением. В двухместных отношениях отношение устанавливается между двумя предметами, в трёхместных – между тремя. Пример контекста с двухместным отношением: «Иван брат Петра», с трёхместным: «Калининград расположен между Вильнюсом и Гданьском».
Далее все признаки делятся на:
– простые и сложные. Простые признаки представляют собой элементарные характеристики отдельно взятых предметов. Выше были приведены примеры простых признаков. Сложные признаки образуются из простых с помощью логических союзов «и», «или», «либо». Примеры сложных признаков: «быть студентом и спортсменом», «делиться на 2 или делиться на 4».
– родовые и видовые. Родовые признаки выделяют исходное множество предметов, видовые – правильные подмножества в исходном множестве. Сложный или простой видовой признак в логике принято называть «видовым отличием». Так, в понятии «слово, обозначающее предмет, которое отвечает на вопрос «кто?» выражение «слово, обозначающее предмет» представляет родовой признак, так как оно выделяет исходное множество слов, обозначающих предметы, а выражение «отвечающее на вопрос «кто?» представляет видовой признак, так как оно выделяет на множестве слов обозначающие предметы, т.е. на множестве существительных его правильное подмножество, т.е. множество одушевлённых существительных.
– положительные и отрицательные.
Положительные признаки указывают на наличие определённых характеристик у предмета, а отрицательные – на их отсутствие. Примеры положительных признаков: высокий, моральный, спокойный, решительный, ленивый; примеры отрицательных признаков: невысокий, аморальный, беспокойный, нерешительный; неленивый.
– существенные и несущественные.
Существенные признаки – это признаки, без которых нельзя составить адекватное понятие о предмете, а несущественные – это такие признаки, без которых можно составить адекватное понятие о предмете вследствие возможности их замены на другие. Например, в понятии «предмет мебели, сделанный из дерева, предназначенный для сидения одного человека, имеющий спинку и не имеющий подлокотников (стул)»* признак «сделанный из дерева» несущественный, так как без этого признака можно составить адекватное понятие о стуле вследствие того, что в данном понятии подразумевается, что этот признак может быть заменён признаком «сделанный из металла», «сделанный из пластмассы». А поскольку в понятии обобщаются предметы из некоторого исходного множества, то признак «сделанный из дерева» можно опустить без ущерба иметь адекватное понятие о стуле. Напротив, признаки «быть предметом мебели», «быть предназначенным для сидения одного человека», «иметь спинку», «не иметь подлокотников» являются существенными, так как они позволяют отличить стул от табурета, дивана и кресла и тем самым составить адекватное понятие о стуле.
– отличительные и неотличительные признаки. Отличительные признаки – это признаки, которые выделяют ровно один класс предметов и присущи только этим предметам. Как правило, один видовой признак редко бывает отличительным. Хотя, например, в понятии «чётное число» имеется лишь один видовой признак – «делиться на два», и он является отличительным. В то же время легко привести примеры из математики, когда один видовой признак присущ разным классам предметов. Например, видовой признак «иметь все прямые углы» присущ и квадратам, и прямоугольникам, равно как и то, что признак «иметь все равные стороны» присущ и ромбам, и квадратам, и треугольникам. Но когда мы образуем из этих признаков один сложный видовой признак (видовое отличие), то он становится отличительным, и с помощью этого признака мы можем выделить ровно один класс предметов, т. е. класс квадратов. Для этого нужно образовать понятие «четырёхугольник (родовой признак), у которого все стороны равны и все углы прямые» (сложный видовой признак). Следует иметь в виду, что в понятиях видовое отличие, представляющее сложный признак, всегда представляет отличительный признак, однако он может быть несущественен. В этом отношении показателен пример представления Платона о понятии человека как существа двуногого и без перьев. Здесь несомненно сложный видовой признак «иметь две ноги и не иметь перьев» является отличительным, однако не является существенным для человека.
Далее, важно помнить точный математический смысл терминов «множество» и «класс». Согласно основоположнику теории множеств немецкому математику Г. Кантору, «множество S есть любое собрание определенных и различимых между собой объектов нашей интуиции либо интеллекта, мыслимых как единое целое» (21, с. 11).
В плане различения физических и метафизических объектов это определение допускает следующую более ясную реконструкцию: множество есть собрание физических либо метафизических объектов, мыслимых как единое целое.
Множества состоят из элементов, т.е. из отдельных объектов. Так, элементами множества книг являются отдельно взятые книги, множества городов – отдельно взятые города.
Пусть a, b, c есть элементы множества, А, В, С есть сами множества. Тогда между элементами и множествами можно установить два отношения: отношение принадлежности элемента множеству, отношение непринадлежности элемента множеству.
Разъяснение 1. а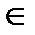 
А, если и только если а входит в А. Пример. Пусть А есть множество городов, а – город Калининград. Тогда отношение между городом Калининградом и множеством городов символически следует выразить в виде а 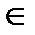А.
Разъяснение 2. а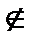 
В, если и только если а не входит в B. Пример. Пусть В есть множество рек, а – город Калининград. Тогда символически отношение между городом Калининградом и множеством рек следует выразить в виде а 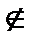В.
Сами множества могут быть либо не быть частями, т.е. подмножествами, других множеств.
При этом в математике различают отношения «быть подмножеством другого множества» либо «быть правильным подмножеством другого множества».
Разъяснение 1. А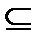 
В (множество А является подмножеством множества В), если и только если каждый элемент множества А является элементом множества В.
Разъяснение 2. А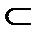 
В (множество А является правильным подмножеством множества В), если и только если каждый элемент множества А является элементом множества В и существует хотя бы один элемент множества В, который не является элементом множества А.
Пример. Пусть А есть множество портовых городов, а В есть множество городов. Ясно, что все портовые города являются городами, т.е. каждый портовый город является городом, но обратное неверно, т.е. не каждый город является портовым. Иными словами говоря, множество портовых городов не совпадает с множеством городов, а представляет его правильную часть, что не имеет места в отношении «множество А является подмножеством множества В», т. е. в отношении А 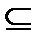В.
Пример. Пусть А есть множество равносторонних треугольников, а В есть множество равноугольных треугольников. Тогда ясно, что каждый равносторонний треугольник является элементом множества равноугольных треугольников. Но верно и обратное: каждый равноугольный треугольник является элементом множества равносторонних треугольников.
Понятно, что для общей практической логики важное значение имеет отношение «быть правильным подмножеством другого множества».
Множества могут быть конечными либо бесконечными. Конечные множества могут задаваться двумя способами:
1. Способом перечисления его элементов. На письме это означает последовательное выписывание элементов множества с заключением их в фигурные скобки {,} на последнем этапе задания множества. Например, пятиэлементное множество первых пяти натуральных чисел на письме будет задано в виде {1, 2, 3, 4, 5}.
2. Путем формулирования некоторого условия, которому должен удовлетворять каждый элемент множества.
Пример. Пусть некоторая фирма набирает охранников, предъявляя к каждому кандидату следующие требования (условия): быть здоровым мужчиной до 35 лет, иметь юридическое образование, владеть табельным оружием, боевыми искусствами, не иметь судимости. Далее фирма проверяет кандидатов на соответствие данным требованиям (условиям) и комплектует группу (множество) охранников. Символически множества, заданные по условию, записываются в виде {х/А(х)}, где А(х) есть формальная запись некоторого содержательного условия. Читается: «Множество элементов х, которые удовлетворяют условию А(х)».
Множества, заданные по условию, называются классами. Из приведенных разъяснений следует, что каждый класс есть множество, но не каждое множество есть класс.
Приведённые уточнения смыслов терминов «предмет», «множество», «класс» позволяют сформировать точное понимание понятия как определённой формы мышления.
Понятия и имена
Мы уже знаем, что логика изучает не любое мышление, а только словесное, вербальное мышление, т.е. мышление, объективированное в языке. Это обстоятельство делает правомерным вопрос: в каких категориях языка представляются понятия в языке?
С позиции общей практической логики в языке целесообразно выделить две языковых категории: имена и повествовательные предложения. Таким образом, вышепоставленный вопрос трансформируется в следующий: представляются ли понятия в языке именами либо они представляются в нем повествовательными предложениями?
Для нахождения ответа на данный вопрос дадим функциональную характеристику в языке именам и повествовательным предложениям.
Предварительно опишем категорию имён. Под именем в логике будем понимать слово либо словосочетание, выделяющее в мире отдельный предмет либо класс предметов. Таким образом, функциональное назначение имени – выделять в мире предметы. Поэтому имена являются адекватной языковой формой представления понятий, которые также выделяют в мире отдельные предметы либо классы предметов. Этим понятия как мысли отличаются от суждений как мыслей. Функциональное назначение суждений заключается в утверждении либо отрицании определенных признаков у предметов. Поэтому суждения не могут быть языковой формой представления понятий. Примеры:
1) Физическое тело – представляет понятие.
2) Некоторые физические тела легче воды – представляет суждение.
Все имена в логике делятся на единичные и общие.[20] В свою очередь, как единичные, так и общие имена делятся на простые и сложные (описательные).
Простые единичные имена называются собственными.
Примеры простых единичных имен в русском языке: Иванов, Петров, Фёдоров, Калининград, Варшава, Брянск, Волга, Десна, Висла, Байкал, Балатон, Выштенец, Машук, Арарат, Казбек, Эверест, Марс, Земля, Венера, 1, 2, 3 и др.
Примеры описательных единичных имен в русском языке: самая длинная европейская река, самое глубокое озеро мира, то небесное тело, которое является естественным спутником Земли, автор романа «Тихий Дон» и др.
Примеры простых общих имён в русском языке: город, река, дом, университет, человек, историк, студент, число, закон, президент, столица и др.
Примеры описательных общих имён в русском языке: четырёхугольник, у которого все стороны равны и все углы прямые; тайное хищение имущества или денег; часть суши, окруженная со всех сторон водой; город, который является административно-политическим центром государства, и др.
Специфической особенностью описательных имён является то, что в них отдельные слова могут обладать интуитивно ясными значениями, которые в совокупности изначально обеспечивают описательному имени наличие ясного самостоятельного смысла.
Данная особенность описательных имен позволяет сделать следующее обобщение языкового представления понятий: понятие есть смысл имени, где смысл есть мысль, представленная в языке.
Деление имён на простые и описательные позволяет также поставить в общей практической логике вопрос о различении ясных и смутных (недостаточно ясных) понятий.
Поскольку описательные имена могут изначально обладать ясным самостоятельным смыслом, объективированным в них через конструкцию словосочетания, то это обстоятельство позволяет классифицировать описательные имена, в которых отдельные слова обладают интуитивно ясным значением, как описательные имена, которые непосредственно представляют в языке ясные понятия.
Что же касается простых имен, то вопрос о том, какие понятия они представляют в языке, решается в зависимости от того, имеются ли для них в языке корректные (удовлетворяющие всем правилам) определения либо ясные описания данных терминов в лексических словарях.
Конкретно это означает, что если для простых имён имеются в языке корректные определения либо их ясные описания в лексических словарях, то они представляют в языке ясные понятия. В противных случаях простые имена представляют в языке смутные понятия.
Понятно, что для успешной научной либо практической деятельности субъекты деятельности должны использовать ясные понятия.
В языке современной логики логическая форма понятия в простейшем случае выражается языковой конструкцией xA(x), которая называется универсалией. Конструкция xA(x) читается: «Предмет x из универсума U такой, что он обладает признаком A(x)». В данной логической форме фиксируются только видовые признаки; родовые признаки исчезают, они трансформируются в фиксирование исходного множества U.
Пример. Выделим логическую форму понятия «город, расположенный в Западной Европе» по схеме универсалии xA(x): город х из множества городов – U, который расположен в Западной Европе – А(х).
Содержание и объём понятия. Диаграммы (круги) Эйлера
Понятия как определённого рода мысли обладают двумя логическими характеристиками: содержанием и объёмом.
В традиционной логике (ТЛ) под содержанием понятия понимают совокупность родовых и видовых признаков, в то время как в современной логике под содержанием понимают совокупность лишь видовых признаков.
При этом в логике различают основное и полное содержание понятия. Так как ТЛ есть часть общей практической логики, то при различении основного и полного содержания понятий мы также будем различать родовые и видовые признаки.
Основное содержание (ОС) понятия – это та минимальная совокупность родовых и видовых признаков, которая необходима и достаточна для того, чтобы выделить в мире определённый класс предметов. Соответственно, полное содержание (ПС) понятия – это совокупность всех признаков, которыми обладает каждый предмет, мыслимый в понятии.
Пример основного содержания (ОС) понятия «квадрат»:
1. быть четырёхугольником (родовой признак);
2. иметь все равные стороны (видовой признак);
3. иметь все прямые углы (видовой признак).
Пример полного содержания (ПС) понятия «квадрат»:
1. быть четырёхугольником;
2. иметь все равные стороны;
3. иметь все прямые углы;
4. иметь взаимно перпендикулярные диагонали;
5. иметь диагонали, которые делятся в точке пересечения пополам.
Под объёмом понятия в логике понимают классы предметов, которые мыслятся в понятии. В самом объёме принято различать элементы объёма и части объёма.
Элементы объёма – это элементы класса предметов, которые выделяются через ОС понятия, а части объёма – это подклассы данного класса предметов.
Пример, иллюстрирующий ОС понятия, его объем, элементы и части объёма.
Пусть мы имеем понятие «населённый пункт, насчитывающий десять либо более тысяч жителей (город)». Число жителей в данном понятии берётся условно.
ОС данного понятия:
1) быть населённым пунктом;
2) иметь десять либо более тысяч жителей.
Элементы объёма данного понятия:Калининград, Брянск, Варшава, Берлин и т.д.
Части объёма данного понятия:портовые города, города Европы, промышленные города, большие города, небольшие города.
Для более ясного понимания соотношения между элементами, частями объёмов и объёмами понятий в логике применяют диаграммы (круги) Эйлера. Леонард Эйлер (1707 – 1783) – немецкий математик, впервые использовал в 1762 г. круг в качестве графической модели объёма понятия, а точку внутри круга – в качестве модели элемента объёма понятия. В дальнейшем диаграммы Эйлера были дополнены в логике моделью исходного множества U в виде четырехугольника.
Пример изображения на кругах Эйлера соотношения между элементом, частью объема и объёмом понятия «город». Пусть U – это исходное множество населённых пунктов, А – понятие «портовый город», В – понятие «город», a – город Калининград. Тогда соотношение между a, А и В на кругах Эйлера будет иметь следующий вид:
| U |
| B |
объем понятия «город»[21]
| A a |
объем понятия «портовый город», часть объема
понятия «город»
г. Калининград, элемент объема понятий
«портовый город», «город»,
«населенный пункт»
Данная диаграмма наглядно показывает, что все портовые города являются городами, но не все города являются портовыми, т.е. показывает, что объём понятия «портовый город» является правильной частью объёма понятия «город».