Проверка совместного действия нормальных, касательных и местных напряжений в месте изменения сечения.

Расчетные нормальные и касательные напряжения в краевом участке стенки балки на уровне поясных швов:

Ϭ₁ = 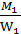* 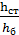= 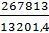* 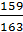= 19.79 кН/см²

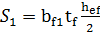= 26*2* 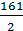= 4186 см³

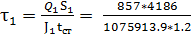= 2.78 кН/см²

Приведенное напряжение в крайних точках стенки на уровне поясных швов:

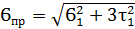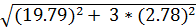= = 20,37 кН/см² ≤ 1,15R_yγ_c = 27.6 кН/cм²

Проверка общей устойчивости балки.

Определяем отношение, при котором можно не проверять устойчивость:

1) В середине пролета балки (балка работает упруго δ = 1)

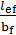= δ[0.41 + 0.0032 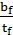+ (0.73 – 0.016 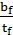) 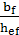] 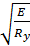= 1*[0.41 + 0.0032 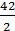+ (0.73 – 0.016 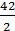) 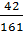] 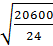= 17,00≥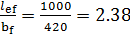

2) В месте уменьшенного сечения балки (балка работает упруго δ =1)

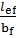= 1*[0.41 + 0.0032 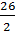+ (0.73 – 0.016 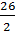) 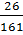] 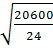= 15,69 ≥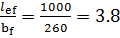

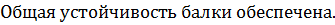
Проверку прогиба балки можно не производить, так как принятая высота балки больше минимальной.

Проверка и обеспечение местной устойчивости элементов балки.

1. Проверка устойчивости сжатого пояса

Производится в месте максимальных нормальных напряжений в нем – в середине пролета балки, где возможны пластические деформации:

Условие обеспечения устойчивости пояса имеет вид:

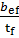≤ 0.5

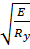
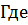
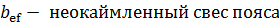
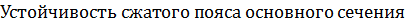
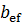= ½(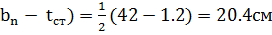

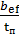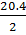= = 10.2 < 0,5 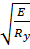= 14.65

2. Устойчивость стенки

Проверяем необходимость укрепления стенки поперечными ребрами жесткости:

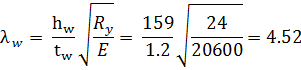
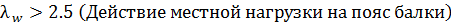
Следовательно, поперечные ребра жесткости необходимы.

Конструкция ребер жесткости:

Расстояние между поперечными ребрами жесткости не должно превышать

2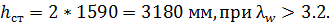

Расстояние между поперечными ребрами жесткости должно быть a < 2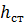

Принимаю односторонние ребра жесткости, располагая их с одной стороны балки. При этом ширина ребер жесткости должна быть не менее:

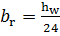+ 50 =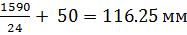

Принимаю ширину ребер жесткости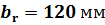

Толщина ребер жесткости должна быть не менее

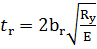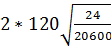= = 8,19 мм

Принимаем толщину ребер жесткости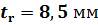

Проверяем устойчивость стенки в зоне действия наибольших нормальных напряжений.

Значение напряжений на уровне поясных швов :

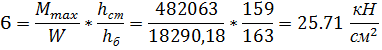
Т.к отношение a/ 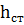= 250/159 = 1.57 > 1.33

Проводим 2 проверки, но в этом случае во 2ой проверке a заменяем на a₁ = 0.67a

1ая проверка:

Определяем критические нормальные напряжения

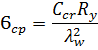
Коэффициент, учитывающий степень упругого защемления стенки в поясах балки и определяемый по формуле:

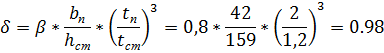
Интерполяцией получаем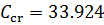

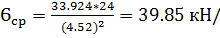см²

р = 1,04 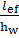=1.04 * 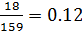– относительная длина загружения пластины местной нагрузкой

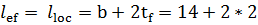= 18 см

b – длина передачи местной нагрузки на балку ( ширина полки балки настила)

С₁ = 13,68

С₂ = 1,98

Далее определяем =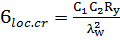

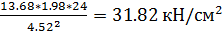
Местные напряжения в стенке под балками:

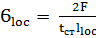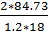= = 7.85

Проверяем условие устойчивости (при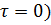

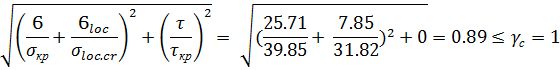
2я проверка:

a₁ = 0.67a = 0.67*2500 = 1675 мм

Тогда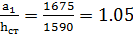

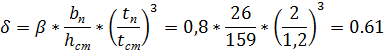
C_cr = 32.976

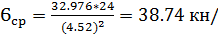см²

p = 0.13 a_1/h_ст = 1,05

С₁ = 17,96

С₂ = 1,786

=

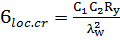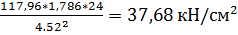
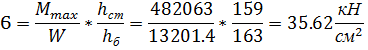
Проверяем условие устойчивости (при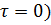

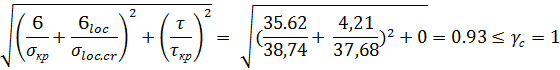
Стенка в середине пролета устойчива.

Рассмотрим сечение, расположенное вблизи от опоры балки на расстоянии

Х = h_w/2 = 159/2 = 79.5 см

M₁ = 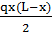= = 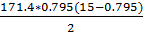967.81 кНм

Q_{1 =} q(L-x) = 171.4(15/2 – 0.795) = 1149.24 кН

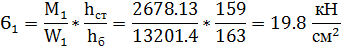
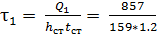= 4.49 кН/см²

Местные напряжения в стенке под балками

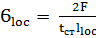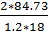= = 7.85 кН/см²

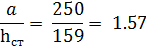
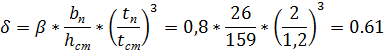
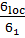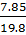= = 0.4

р = 1,04 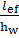=1.04 *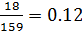

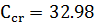
С₁ = 13,68

С₂ = 1,8

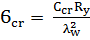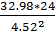= = 38.74 кН/см²

=

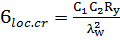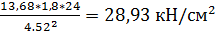
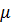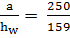= = 1.57

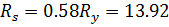
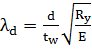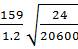= = 4.52

Определяем критические касательные напряжения

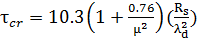= 10.3(1 + 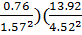) = 8.93 кН/см²

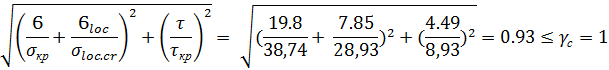
Приведенные проверки показали, что запроектированная балка удовлетворяет требованиям прочности, прогиба, общей и местной устойчивости.