Знакомство с понятием“Решение тригонометрических уравнений, сводящихся к квадратным”с применением стратегии “Кластеры”.
Тут необходимо использовать прием- кластеры («гроздья»). С каждым шагом они могут записывать те или иные моменты по очереди(от простого к сложному). На случае если ученик забыл или не понял материал он может подсмотреть в свою схему(опираясь на неё). Это поможет ему крепко усвоить материал. Схема:
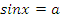 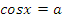 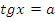 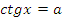 |
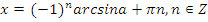 |
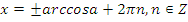 |
 |
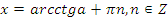 |
Тип урока: комбинированный.
Цели урока:
Образовательные:
- вспомнить методы решения простейших тригонометрических уравнений и обеспечить их применение при решении задач вариантов ЕНТ;
- изучить метод замены тригонометрической функции для решения некоторых видов тригонометрических уравнений;
- закрепить навыки решения простейших тригонометрических уравнений;
Развивающие:
- продолжать содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать;
- продолжать формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения;
- продолжать отрабатывать навыки самооценивания знаний и умений, выбора задания, соответствующего их уровню развития.
Воспитательные:
- вырабатывать самостоятельность при работе на уроке;
- способствовать формированию активности и настойчивости, максимальной работоспособности.
Структура урока:
1. Вводно-мотивационная часть.
1.1. Организационный момент.
1.2. Устная работа.
2. Основная часть урока.
2.1. Повторение (чередование фронтальной и индивидуальной форм работы с последующей проверкой задания).
2.2. Знакомство с новым способом решения тригонометрических уравнений.
3. Рефлексивно-оценочная часть урока.
3.1. Обсуждение результатов индивидуальной работы.
3.2. Информация о домашнем задании.
3.3. Подведение итогов урока.
Ход урока
Вводно-мотивационная часть
1.1.Организационный момент.
Задачи этапа: обеспечить внешнюю обстановку для работы на уроке, психологически настроить учащихся к общению.
Содержание этапа:
1. Приветствие.
Учитель: Здравствуйте, садитесь! Запишите сегодняшнее число и тему урока. “Метод замены для решения некоторых тригонометрических уравнений”. Задания по решению тригонометрических уравнений встречаются в вариантах ЕНТ.
2. Проверка готовности учащихся к уроку.
Учитель: Ребята, кто сегодня отсутствует? Все готовы к уроку? Итак, внимание. Начинаем!
3. Озвучивание целей урока и плана его проведения.
Учитель: Тема нашего урока - решение тригонометрических уравнений. Я думаю, вам будет интересно на уроке.
Цель урока сегодня – вспомнить метод решения простейших тригонометрических уравнений, решение квадратных уравнений и изучить, как с помощью замены тригонометрических функций сводить некоторые тригонометрические уравнения к квадратным.
В начале урока мы вспомним методы решения квадратных уравнений, числовые значения тригонометрических функций, основные формулы тригонометрии, формулы решения простейших тригонометрических уравнений.
После каждого блока заданий будем проводить разноуровневые проверочные работы, задания которых вы будете выбирать самостоятельно, учитывая свои знания, умения и навыки. Проверяем решения, и вы выставляете себе оценку за каждый вид заданий.
После чего познакомимся с тем, как с помощью замены переменных сводить некоторые тригонометрические уравнения к квадратным. Обсудим полученные результаты работы на уроке, оценим индивидуальную работу. Затем получите инструктаж по выполнению домашнего задания и подведем итоги урока. Согласны с таким планом работы? Хорошо! Итак, приступаем.
1.2. Устная работа.
Задачи этапа: создать базу для усвоения понятий, которые будут использованы на уроке.
Содержание этапа:
Учитель: Первое задание для устной работы - решите уравнения:
| Уравнения | Ответ |
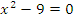 | -3, 3 |
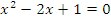 | |
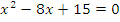 | 3, 5 |
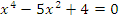 | -2, -1, 1, 2 |
Учитель: Второе задание – используя основные формулы тригонометрии, упростите выражение:
| Выражение | Ответ |
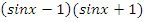 | 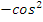 x x |
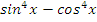 | 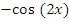 |
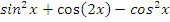 | |
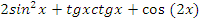 | 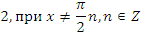 |
Основная часть урока.
2.1. Повторение (чередование фронтальной и индивидуальной форм работы с последующей проверкой задания).
Задачи этапа: обеспечивать развитие у учащихся общеучебных умений и навыков: умение анализировать, синтезировать, сравнивать, обобщать, поиск способов решения, отрабатывать навыки самооценивания знаний и умений, выбора разноуровневого задания.
Содержание этапа:
Учитель: Ребята, давайте вспомним свойства четности и нечетности тригонометрических функций и значения тригонометрических функций для различных чисел.
Учащиеся формулируют свойства четности и нечетности, называют табличные значения тригонометрических функций.
Учитель: А теперь выполним самостоятельную работу. Работа предлагается в 2 вариантах, после чего проверим правильность ее выполнения.
Найдите значения тригонометрических выражений:
| 1 вариант | 2 вариант | ||
| Вычислить | Ответ | Вычислить | Ответ |
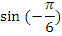 | 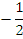 | 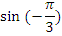 | 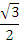 |
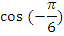 | 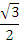 | 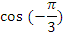 |  |
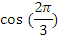 | 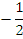 | 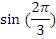 | 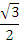 |
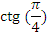 | 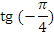 | -1 | |
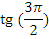 | Нет | 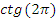 | нет |
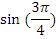 | 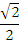 | 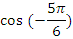 | 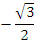 |
Учитель: А теперь сверьте свои ответы с ответами соседа. Сверили. Молодцы!
Учитель: Ребята, проверьте правильность ответов и оцените свои работы согласно шкале:
| Количество верных ответов | Оценка |
| <4 |
Учитель: Ребята, а теперь перейдем к решению простейших тригонометрических уравнений. Напомните, пожалуйста, формулы решения уравнений вида: 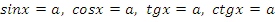 , при
, при 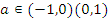 .
.
Учащиеся называют формулы решения уравнений
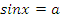 | 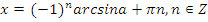 |
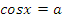 | 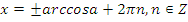 |
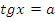 |  |
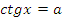 | 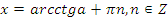 |
2.2. Введение нового способа решения тригонометрических уравнений.
Задачи этапа: организовать деятельность учащихся по применению знаний, умений и навыков при решении тригонометрических уравнений незнакомыми способами.
Содержание этапа:
Учитель: А сейчас познакомимся с решением тригонометрических уравнений новым способом: с помощью замены одной из тригонометрических функций и сведением к квадратному уравнению.
| Вид уравнения | Подходящая замена | |
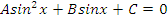 | 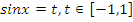 | |
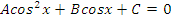 | 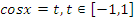 | |
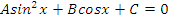 | 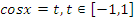 | |
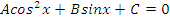 | 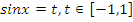 | |
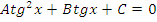 | 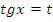 | |
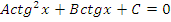 | 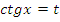 | |
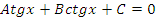 | 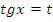 или или 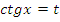 |
В таблице приведены виды тригонометрических уравнений и подходящая замена переменной, с помощью которой данные уравнения могут быть сведены к квадратным. Чтобы не заучивать таблицу, давайте выделим признаки, по которым произвольное тригонометрическое уравнение может быть классифицировано, как уравнение, сводящееся к квадратному.
Первым действием нужно убедиться, что все тригонометрические функции, входящие в уравнение, имеют единый аргумент. Если это не так, то их нужно свести к единому аргументу. Для этого используются формулы блока: “формулы двойного аргумента”
Вторым действием нужно пытаться привести уравнение виду: 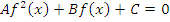 , где
, где 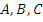 – некоторые числа,
– некоторые числа, 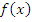 – одна из тригонометрических функций. Для этого используется основное тригонометрическое тождество или взаимосвязь между тангенсом и котангенсом.
– одна из тригонометрических функций. Для этого используется основное тригонометрическое тождество или взаимосвязь между тангенсом и котангенсом.
Третьим действием общая тригонометрическая функция заменяется буквой 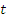 , при этом учитывается область значений обозначаемой функции.
, при этом учитывается область значений обозначаемой функции.
Таким образом, некоторые тригонометрические уравнений могут быть сведены к видам из таблицы.
Учитель: разберем несколько примеров:
1) 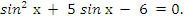
Данное уравнение соответствует (1) таблицы, поэтому делаем замену 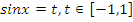 ,
,
· получаем квадратное уравнение: 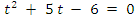 ,
,
· находим корни 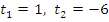 ,
,
· замечаем, что 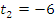 посторонний корень, поскольку
посторонний корень, поскольку 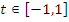 ,
,
· делаем обратную замену, т.е. решаем уравнение 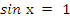 , у которого корнями будут числа
, у которого корнями будут числа 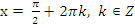 .
.
Ответ: 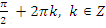 .
.
2) 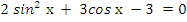 .
.
Данное уравнение соответствует (3) таблицы, поэтому cделаемзамену 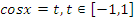 . Из основного тригонометрического тождества следует, что
. Из основного тригонометрического тождества следует, что 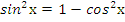 ,
, 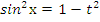 ,
,
· получим квадратное уравнение: 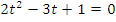 ,
,
· находим корни: 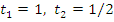 ,
,
· делаем обратную замену:
· 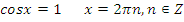 или
или
· 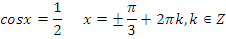
Ответ: 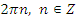 ,
, 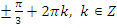 .
.
3) 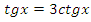 .
.
Данное уравнение соответствует (7) таблицы, поэтому можно сделать замену 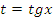 или
или 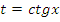 . После решения примера самостоятельно сделайте другую замену и сравните ответы.
. После решения примера самостоятельно сделайте другую замену и сравните ответы.
Сделаем, например, замену 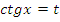 , вспомним, что
, вспомним, что 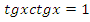 , поэтому
, поэтому 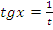 , получим уравнение
, получим уравнение 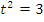 , откуда
, откуда 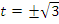 или, делая обратную замену,
или, делая обратную замену, 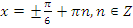 .
.
Ответ: 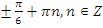 .
.
4) 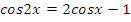 .
.
Данное уравнение непосредственно не имеет вид, описанный в таблице. Как правило, легко классифицировать уравнения, если привести тригонометрические функции в него входящие к одному аргументу. Поскольку 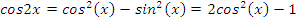 , то уравнение сведено к (2) виду таблицы. Поэтому делаем замену
, то уравнение сведено к (2) виду таблицы. Поэтому делаем замену 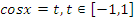 и получаем неполное квадратное уравнение
и получаем неполное квадратное уравнение 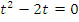 , откуда
, откуда 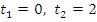 . (
. ( 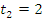 посторонний корень, поскольку
посторонний корень, поскольку 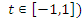 .
.
Делаем обратную замену:
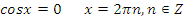
Ответ: 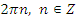 .
.
Учитель: А теперь выберите одно из предложенных уравнений и самостоятельно решите его.
| На оценку | 1 вариант | |
| задание | ответ | |
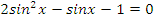 | 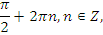 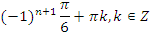 | |
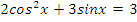 | 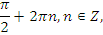 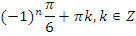 | |
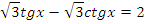 | 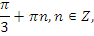 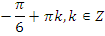 | |
| 2 вариант | ||
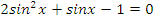 | 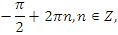 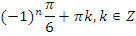 | |
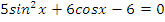 | 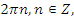 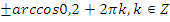 | |
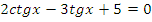 | 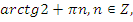 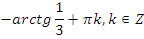 |
Учитель: “А теперь проверьте работу соседа, поставьте оценку”.
Выписываются на доске ответы. Учитель: проверьте правильность собственного решения и правильность проверки примера соседа.
