Непрерывности регрессии выступает
как признак экспериментального эффекта1
Основные идеи плана с нарушением непрерывности регрессии будет легче понять, если мы сначала рас-
_____________________________________________________________________________
1 В данном разделе использованы материалы, опубликованные в работах: C a m p b e l l D. T. Quasi-Experimental Desings. — In: Social Experimentation: A method for planning and evaluating social innovations. Ed. by H. W. Riecken and R. F. Boruch. N. Y., Academic Press, 1974. © Academic Press, Inc., 1974, C a m p b e l l D. T. Reforms as Experiments. — In: Reading in evaluation research. Ed. by F. G. C a r o, N Y., Russell Sage Foundation, 1977. © Sage Publications, Inc, 1977. — Прим. ред.
смотрим сильную и слабую формы одного истинного эксперимента, применимого к ситуациям того же типа, что и обсуждаемый квазиэксперимент. Напомним, что одним из непременных условий проведения социального эксперимента является невозможность предоставления всем желающим определенных благ, выступающих в роли экспериментальных воздействий. Это гарантирует, что число экспериментальных единиц (испытуемых, школ, городов и т. д.), готовых подвергнуться воздействию, превышает число таких единиц, которые фактически могут быть им охвачены. Данное условие, как правило, выполняется для пилотажных программ, которые применяются к подгруппам популяции, выделенным по принципу больших заслуг или большей нуждаемости. Если число кандидатов превышает количество предусмотренных программой мест, то обеспечивается выполнение одного из условий для формирования контрольной группы из части кандидатов.
В этих условиях лучшая стратегия состояла бы в проведении истинного эксперимента — в составлении экспериментальной и контрольной групп путем рандомизации, охватывающей весь ранговый ряд «достойности». Рассмотрим, например, программу профессиональной подготовки полностью или частично безработных молодых людей для получения ими определенной хорошо оплачиваемой работы. Критерием отбора может служить (и одно время действительно служил) доход на одного члена семьи кандидата. Если число «достойных» кандидатов, подавших заявление о приеме, больше числа вакансий, то администратор, ориентированный на эксперимент, мог бы отобрать будущих участников из всех «достойных» случайным образом. Учитывая выборочные данные эквивалентных оставшихся кандидатов для формирования из них контрольной группы, он мог бы в дальнейшем получить сведения о заработках тех, кто прошел и кто не прошел подготовку, и измерить ее эффект.
Но во многих случаях рандомизированный отбор «достойных» считается неприемлемым. При этом ссылаются на то, что признак, по которому производится отбор, не дихотомичен, а имеет различные степени выраженности. Если возможности слишком ограничены, чтобы принять всех кандидатов, то места должны быть
предоставлены наиболее нуждающимся и наиболее «достойным». Этот довод против рандомизации часто приводится, как если бы существующие процедуры распределения кандидатов действительно удовлетворяли требованиям равенства, в свете которых рандомизация якобы оказывается несостоятельной. Тщательное изучение работы соответствующих учреждений показало бы в большинстве случаев, что они не удовлетворяют этим требованиям. Процедура ранжирования «достойных» кандидатов по степени «нуждаемости», на которой основывалось бы решение о приеме, обычно отсутствует. Случайность процедур отбора и распределения делает возможным то, что кандидаты могут зачисляться в значительной степени по соображениям удобства администрации или просто по знакомству. Чтобы избежать чрезмерного потока заявлений, вновь открывающимся возможностям дается минимальная огласка. Если применяется правило «первым пришел — первым обслужен», то наиболее нуждающиеся редко оказываются среди тех, кто внимательно следит за новыми возможностями, а «пришедшие первыми» узнают о них по неофициальным каналам, еще до опубликования соответствующего объявления. В отличие от существующей практики широкая огласка программы, приводящая к избытку кандидатов, которые затем в случайном порядке отбираются для участия в программе или входят в контрольную группу, представляла бы собой высокоморальную процедуру, помимо и сверх того, что она делала бы возможным экспериментальное оценивание.
Однако если нельзя преодолеть сопротивление полной рандомизации, то все же можно провести слабую форму этого эксперимента, а именно эксперимент с «рандомизацией, разрывающей ранговую связку», в котором особое внимание уделяется степени достойности.
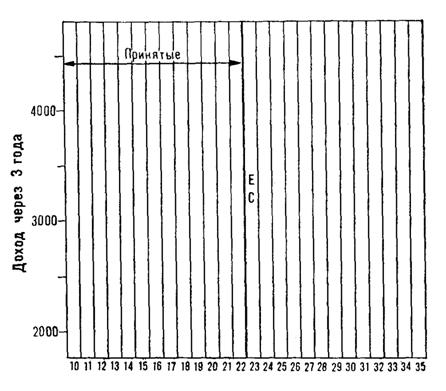
Предположим, что отбор участников программы производится не из всех кандидатов, а сконцентрирован на наиболее нуждающихся, причем мест хватает как раз для приема всех тех, чей недельный доход на каждого члена семьи составляет 22 доллара и ниже, плюс еще половину тех, для кого эта цифра равна 23 долларам. Теперь, не нарушая ограничения, согласно которому программа предназначается наиболее нуждающимся,
можно рандомизировать отбор из тех, кто попал в ранговую связку «23 доллара». Таким образом удается провести небольшой истинный эксперимент. Правда, это слабый эксперимент в двух отношениях. Во-первых, в нашем распоряжении оказывается очень малое число случаев, и, следовательно, различие, отражающее подлинный эффект, может оказаться статистически незначимым или даже иметь противоположный знак из-за флюктуаций выборочных показателей. Естественно, возникает желание максимально увеличить число лиц, приходящихся на пограничную ранговую связку, для чего можно расширить интервал значений критерия отбора, внутри которого они считаются практически равными. Так, в настоящем примере интервал в 2 доллара дает большее число связанных рангов, чем, скажем, интервал в 50 центов, и к тому же позволяет избежать чрезмерной и бессмысленной точности в последнем случае. Другая слабость этого эксперимента состоит в том, что он исследует эффект воздействия только для узкого класса значений критерия отбора и поэтому позволяет лишь в ограниченной степени судить об эффекте по всему диапазону значений этого критерия (см. рис. 4). Правда, исследуемый узкий интервал вряд ли сильно отличается от соседних интервалов, которые могли бы стать граничными в случае возможного расширения или сокращения программы, и, следовательно, получаемые данные существенны для принятия важных административных решений.
При рассмотрении рис. 4 возникает вопрос: какова дальнейшая судьба тех, для кого значение критерия отбора (k) слегка отличается от граничного? Считая программу подготовки эффективной, можно было бы ожидать, что полностью включенная в эксперимент категория лиц с показателем k, равным 22 долларам, будет в дальнейшем иметь доход, весьма близкий к доходу экспериментальной (Е) подгруппы с k = 23 долларам — возможно, чуть ниже, соответственно несколько меньшему начальному доходу, но все же выше, чем для контрольной группы (С) с k = 23. Аналогично дело будет обстоять и для k, равных 21, 20 и ниже. С другой стороны, дальнейшие доходы лиц с k = 24 (никто из них не участвовал в эксперименте) должны быть примерно такими же, как и у членов контрольной группы
Недельный доход на одного члена семьи
Р и с. 4. Результат гипотетического эксперимента по плану с разрывом ранговой связки, в котором одни кандидаты с недельным доходом 23 доллара на одного члена семьи принимаются в случайном порядке на курсы профессиональной подготовки, а другие образуют контрольную группу. Все кандидаты с доходом 22 доллара и ниже проходят подготовку. Средний заработок испытуемых спустя 3 года отмечен буквами Е и С соответственно для экспериментальной и контрольной
группы.
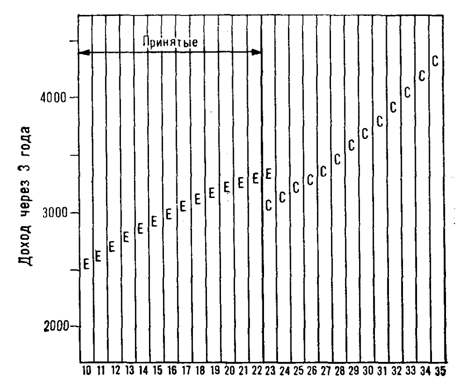
с k = 23 — чуть выше, но не как у членов экспериментальной группы с k = 23 и т. д. На рис. 5 представлены гипотетические результаты такого прослеживания последующих доходов по всем значениям k.
Сравнение рис. 5 и 4 наводит на мысль о том, что результаты гипотетического эксперимента с рандомизацией ранговой связки можно вывести из анализа эффектов при неслучайном назначении воздействия по всему диапазону значений критерия отбора k. Так, если принятыми оказываются все лица с доходом в 22 доллара и ниже, а категория «23 доллара» целиком остается вне воздействия, то, получив результат, изображенный на рис. 6, мы могли бы с полной уверенностью считать, что эксперимент с рандомизацией ранговой связки привел бы к результатам, показанным на рис, 4 и
Недельный доход на одного члена семьи
Р и с. 5. Данные гипотетического эксперимента по плану с разрывом ранговой связки для различных категорий доходов на члена семьи (включая данные, представленные на рис. 4). Все кандидаты с доходом 22 доллара и ниже получили подготовку на данных курсах, и никто не был
принят, если доход на одного члена семьи составлял 24 доллара и выше.
5. В то же время результаты, представленные на рис. 7, указывали бы на отсутствие эффекта воздействия.
Рис. 6 и 7 иллюстрируют использование нарушения непрерывности регрессии в качестве признака экспериментального эффекта1. Этот квазиэксперимент может заменить эксперимент с разрывом ранговой связки, но не с рандомизацией, распространенной на весь диапазон значений k. Результаты анализа не предназначены для оценки эффектов при любых значениях критерия
_____________________________________________________________________________
1 См., например, работы: T h i s t l e t h w a i t e D. L. and C a m p b e l l D. T. Regression-discontinuity analysis: An alternative to the ex post facto experiment. — «Journal of Educational Psychology», I960, v. 51, p. 309—317: C a m p b e l l D. T. Reforms as experiments. — «Amer. Psychologist». 1969, v. 24, p. 409—429; G o l d b e r g e r A. S. Selection bias in evaluating treatment effects: Some formal illustrations. Madison, Institute for Research on Poverty, Univ. ofWisconsin. 1972.
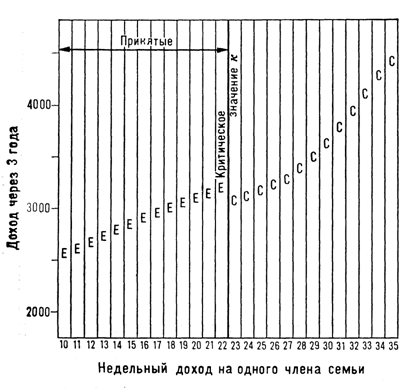
Р и с. 6. Гипотетические данные эксперимента по плану, в котором используется нарушение непрерывности регрессии в качестве показателя экспериментального эффекта. Эффект курсов профессиональной подготовки тот же, что и на рис. 4 и 5. Рис. 6 в принципе идентичен рис. 5, с той лишь разницей, что здесь отсутствует рандомизируемая категория кандидатов и рандомизация ранговой связки. Вместо этого на курсы приняты те, чьи доходы составляли 22 доллара на одного
члена семьи и ниже.
отбора и лишь служат основой для экстраполяции результатов гипотетического эксперимента с разрывом ранговой связки в данной критической точке.
План 16 является квазиэкспериментальным в том смысле, что по сравнению со случаем рандомизации ранговой связки при интерпретации данных приходится делать предположения, менее доступные проверке. Например, необходимо предположить однородность единиц измерения по обе стороны от критической точки. Требуется также сделать ряд предположений о виде функции регрессии. Предлагаемый способ статистического анализа 1состоит в подборе линий регрессии от-
_____________________________________________________________________________
1 Разработан, в частности, Д. А. Суином в диссертации, подготовленной в Северо-Западном университете.
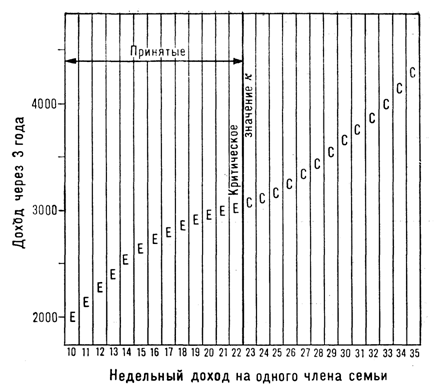
Р и с. 7. Гипотетический результат эксперимента по плану с нарушением непрерывности регрессии
в условиях, аналогичных рис. 5 и 6, для случая, когда эффект воздействия полностью отсутствует.
дельно для двух сегментов, данных слева и справа от критической точки, с последующим определением величины скачка путем экстраполяции каждой кривой за критическую точку. Разность между двумя экстраполированными значениями, очевидно, будет зависеть от предполагаемой формы каждой кривой. В случае двух сигмоид, изображенных на рис. 6 и 7, использование линейной функции регрессии при наличии данных, представленных на рис. 7, даст псевдоэффект. Наряду с численной обработкой данных рекомендуется также представлять данные в виде графика и не доверять результатам статистических расчетов, если вид его указывает на правдоподобность непрерывной функции, не имеющей разрыва в критической точке. Нельзя, конечно, исключить случайного совпадения независимого скачка линии регрессии с критической точкой. Но это маловероятно, если обосновано предположение о равенстве интервалов шкалы измерения и частоты внутри интервалов распределены равномерно.
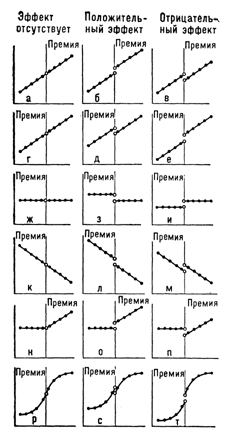 На рис. 8 приведены всевозможные гипотетические результаты применения плана 16, причем графики, помещенные слева, отвечают отсутствию эффекта, а те, что в центре и справа, — наличию положительного или отрицательного эффекта. Словом «премия» повсюду обозначена область значений критерия отбора k, соответствующая экспериментальной группе. Если премия назначается по принципу больших заслуг (рис. 8а, б), то сравнение показателей в области критической точки без учета регрессии данных конечного тестирования по k приводит к оптимистическим псевдоэффектам: на рис. 8а получившие премию в дальнейшем больше преуспевают, но не благодаря ей. Ситуация помощи нуждающимся обычно соответствует рис. 8 г, д. Здесь,
На рис. 8 приведены всевозможные гипотетические результаты применения плана 16, причем графики, помещенные слева, отвечают отсутствию эффекта, а те, что в центре и справа, — наличию положительного или отрицательного эффекта. Словом «премия» повсюду обозначена область значений критерия отбора k, соответствующая экспериментальной группе. Если премия назначается по принципу больших заслуг (рис. 8а, б), то сравнение показателей в области критической точки без учета регрессии данных конечного тестирования по k приводит к оптимистическим псевдоэффектам: на рис. 8а получившие премию в дальнейшем больше преуспевают, но не благодаря ей. Ситуация помощи нуждающимся обычно соответствует рис. 8 г, д. Здесь,
если не принять во внимание наличие регрессии, программа может показаться вредной в отсутствие эффекта или неэффективной, если имеется реальный эффект.
План 16, разумеется, работает ничуть не хуже, если критерий отбора k статистически не связан с данными, полученными после воздействия (премии), как в примерах рис. 8 ж, и. В таких случаях признак, по которому производится отбор, является функциональным экви-
Р и с. 8. Примерные данные экспериментов типа 16.
валентом рандомизации. Очевидно, возможна и отрицательная регрессия (рис. 8к, м). Рис. 8 н, п приведены с целью подчеркнуть тот факт, что именно скачок регрессии в критической точке является признаком эффекта, тогда как различие в наклоне кривой без такого скачка еще не свидетельствует о наличии эффекта. Это становится более очевидным, если мы вспомним, что в случаях типа н эксперимент с рандомизацией ранговой связки показал бы отсутствие эффекта. Криволинейная регрессия (рис. 8 р—т) может вызвать дополнительные трудности в интерпретации результатов, поскольку из-за выборочной ошибки случай, показанный на рис. 8 р, может быть принят за случай 8 б.
Следующая иллюстрация, рис. 9, содержит данные машинного эксперимента — имитированные индивидуальные наблюдения и построенные для них линии регрессии — в отсутствие эффекта и представляет собой более подробный вариант рис. 8 а. Рис. 10 показывает наличие эффекта. Данные предварительного тестирования генерировались путем приписывания каждому индивиду взвешенной нормальной случайной величины, игравшей роль «истинного значения», к которому добавлялась взвешенная независимая случайная «ошибка». «Истинное значение тестового показателя» в сумме с другой независимой «ошибкой» имитировали результаты итогового тестирования для случаев отсутствия эффекта (рис. 9). Эффект воздействия имитировался введением соответствующей добавки для тех «испытуемых», которые «подверглись воздействию», то есть для значений k, превышающих критическое значение.
Хотя приведенные иллюстрации относятся к случаю одной зависимой и одной независимой переменной, часто предпочтительны многомерные варианты данного эксперимента, если при этом не утрачивается четкость правила отбора. Многомерные переменные, характеризующие последующее состояние испытуемых, можно использовать разными способами. Так, можно ввести статистические поправки для одной из зависимых переменных (такой, как более поздние заработки) в целях устранения дифференциальных эффектов различных социально-экономических фоновых переменных, кроме тех, которые были использованы при выработке количественного критерия отбора. Вместо этого можно
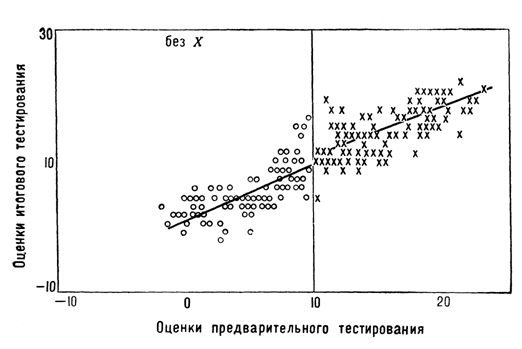
Р и с. 9. Данные машинного эксперимента типа 16: эффект отсутствует.
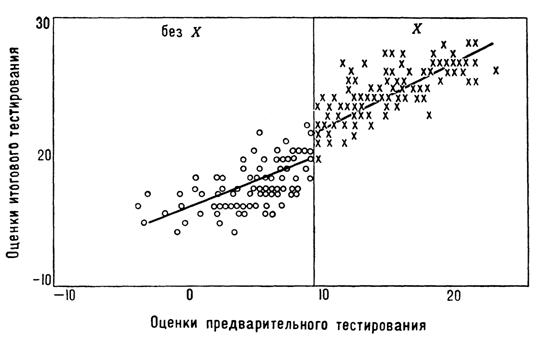
Р и с. 10. Данные машинного эксперимента типа 16: эффект имеет место.
представить результат в виде составной переменной и применить технику множественной регрессии.
Бросим теперь взгляд на строку табл. 3, соответствующую плану 16. Ввиду синхронности экспериментального и контрольного режимов фоновая стимуляция и естественное развитие находятся под контролем. Главный эффект тестирования контролируется, поскольку оно осуществляется одинаково как в экспериментальной, так и в контрольной группе. Инструментальные погрешности могут создать известные трудности, если итоговое тестирование проводится под эгидой той же организации, которая ведала отбором кандидатов: благодарность счастливчиков и горечь обойденных может привести к различиям в выражении ими своих установок, к различной степени преувеличения собственных успехов. Этот недостаток присущ также истинному эксперименту с разрывом ранговой связки. Этот фактор можно проконтролировать, поручив продолжение исследования другой организации. Мы считаем, что, согласно приведенным выше соображениям, эффекты регрессии и состава групп не могут повлиять на интерпретацию результатов, даже, несмотря на неэквивалентность групп и наличие регрессии. Оба фактора контролируются путем детального представления соответствующих зависимостей, а не посредством уравнивания групп. Фактор выбывания будет сказываться, если последующее тестирование и распределение благ производится одной и той же организацией: получившие премию или место на курсах будут, по всей видимости, более охотно сотрудничать, чем те, кто оказался в контрольной группе. Между прочим, похвальное в обычных условиях стремление к репрезентативному опросу всей намеченной выборки может оказаться здесь дезориентирующим. Если, например, рассылка анкет со штампом другой организации ведет к снижению готовности сотрудничать с 90 до 50%, то экспериментатор может отнестись к этому отрицательно, так как он стремился к 100%-ному охвату получивших премию. Он готов забыть, что его действительная цель — получить поддающиеся интерпретации данные, что никакие цифры нельзя интерпретировать изолированно и что использовать данные по премированным можно лишь при наличии сопоставимой контрольной группы. По
этой причине, а также из-за опасности инструментальной погрешности привлечение независимой организации с научной точки зрения предпочтительнее, а 50%-ный возврат анкет из обеих групп лучше, чем 90%-ный из экспериментальной и 50%-ный из контрольной группы. Проблема выбывания остается в силе и для истинного эксперимента с разрывом связки. Для обоих экспериментальных планов угроза внутренней валидности со стороны взаимодействия состава групп и естественного развития находится под контролем. В случае квазиэксперимента это объясняется невозможностью отнести явный скачок регрессии на счет такого взаимодействия. Угроза внешней валидности со стороны взаимодействия между эффектом тестирования и X контролируется постольку, поскольку основные измерения, используемые для принятия решения об отборе кандидатов, являются частью генеральной совокупности, на которую предполагается распространить выводы.
Внешняя валидность истинного эксперимента с рандомизацией ранговой связки и нарушением непрерывности регрессии особенно зависит от взаимодействия между составом групп и X. Иначе говоря, эффект демонстрируется только для очень узкого класса значений k, равных критическому. Однако в случае квазиэксперимента возможности делать заключения, по-видимому, шире.
Корреляционные планы и планы EX POST FACTO
Одним из признаков квазиэксперимента, все отчетливее выступавшим при обсуждении последних девяти планов, является то, насколько экспериментатор может управлять воздействием X, то есть вторгаться в нормальный ход событий. Разумеется, чем больше он контролирует X, тем больше он приближается к осуществлению истинного эксперимента. Это особенно справедливо в отношении планов 7 и 10. Планы 7, 10, 12, 13 (но не 13а) и 14 применимы как в случае естественно возникающих воздействий, так и в случае воздействий, намеренно вводимых экспериментатором. Там, где X остается вне контроля, эксперимент вызывал бы больше подозрений, и те, кто еще согласился бы назвать квази-
экспериментом его варианты с воздействием, контролируемым экспериментатором, не захотели бы применять этот термин к случаям неуправляемого воздействия. Не вдаваясь в обсуждение этого вопроса, подчеркнем только ценность анализа результатов неуправляемого воздействия по типу анализа экспериментальных данных по сравнению с некоторыми вводящими в заблуждение оценочными описаниями и рассуждениями, к которым слишком часто прибегают в подобных случаях.
План 15 прямо предназначен для изучения эффектов естественно возникающих X, но планы, обсуждаемые в этом параграфе (их, правда, чаще именуют не планами квазиэксперимента, а планами анализа данных), еще более интегрированы в естественной обстановке. Мы начнем наше изложение с простого корреляционного анализа, затем перейдем к двум, в общем, приемлемым планам, а в конце подробнее остановимся на исследованиях ex post facto, которые даже в лучшем исполнении признаются неудовлетворительными.
