И тестирования, осуществляемого

Только после воздействия

Хотя идея предварительного тестирования глубоко проникла в сознание исследователей, работающих в об­ласти педагогики и психологии, оно не является неотъ­емлемой частью истинного эксперимента. По причинам психологического порядка трудно отказаться от того,

чтобы удостовериться в «равенстве» экспериментальной и контрольной групп до введения дифференцированного режима эксперимента. Тем не менее, наиболее адекват­ной во всех отношениях гарантией отсутствия изначаль­ного смещения между группами является рандомизация. В рамках доверительных пределов, устанавливаемых статистической моделью, рандомизации достаточно и без предварительного тестирования. Фактически почти все агробиологические эксперименты, выдержанные в традициях работ Фишера [37, 38], выполнены без пред­варительного тестирования. Проводя педагогические ис­следования, особенно в младших классах, часто прихо­дится испытывать методы изложения ученикам совер­шенно нового учебного материала, и в этой обстановке предварительное тестирование в обычном смысле слова невозможно. Точно так же при исследовании влияния доводов адвокатов на решение присяжных неуместно определять априорные оценки виновности или невинов­ности подсудимого. Схема 6 годится для этих случаев, а также для тех, в которых можно было бы применить планы 4 или 5, позволяющие производить подлинную рандомизацию. Вот как выглядит план 6:

R X O₁

R O₂.

Хотя этот план применялся еще в 20-х годах, он не ре­комендуется большинством руководств по методам ис­следования в педагогике. Причина этого отчасти в не­умении отличить его от плана 3, а отчасти в недоверии к рандомизации как средству уравнивания. Этот план представляет собой как бы половину плана Соломона, и, как нетрудно видеть, в нем контролируется как глав­ный эффект тестирования, так и его взаимодействие с X, но в отличие от плана 5 они не измеряются. Однако такое измерение несущественно для решения централь­ного вопроса о наличии эффекта X. Таким образом, хотя план 5 предпочтительнее плана 6 по упомянутым причинам, выигрыш от плана 5 может не стоить боль­шого труда, затрачиваемого на его реализацию. Анало­гично план 6 обычно лучше плана 4, если только нет оснований сомневаться в подлинности рандомизации. Эксперимент типа 6 слишком редко применяется в пе­дагогике и психологии.

Если, как это часто бывает при проведении педаго­гических исследований, доступны данные, полученные до введения X, ими, разумеется, следует воспользоваться формирования блоков, определения факторных уровней или как сопутствующими переменными. Этот совет основан на двух соображениях. Во-первых, статистические модели, соответствующие плану 4, обладают большей мощностью, чем те, которые применимы для плана 6. Хотя значительные усилия, необходимые для реализации плана 4, в большинстве ситуаций делают подобный выигрыш неоправданным, положение меняет­ся, когда нужные исходные показатели «лежат на по­верхности». Во-вторых, доступность таких показателей позволяет проверить наличие взаимодействия X сна­чальным уровнем и тем самым составить более полное представление о возможности обобщения результатов. Правда, нечто подобное может быть выполнено и в рам­ках плана 6, если вместо предварительного тестирования воспользоваться другими имеющимися данными. Кроме того, для генеральной совокупности, на которую предполагается распространять выводы педагогическо­го исследования, характерно частое тестирование. По­следние два обстоятельства могут изменить ситуацию, делая план 6 предпочтительнее плана 4. Отметим так­же, что при заметном выбывании испытуемых между R и итоговым тестированием исходные данные в пла­не 4 обеспечивают больше возможностей для откло­нения гипотезы о влиянии на эффект неравномер­ности выбывания из экспериментальной и контрольной групп.

Как бы то ни было, существует ряд проблем, при­менительно к которым предварительное тестирование невозможно, неуместно или легко провоцирует нежела­тельную реакцию испытуемых; для исследования этих проблем более приемлем план 6. Кроме упомянутого ранее изучения способов подачи нового учебного мате­риала, можно привести много примеров, когда: 1) Х и итоговое тестирование О могут быть предъявлены уча­щимся или группам естественным образом в единой композиции и 2) предварительное тестирование нельзя провести должным образом. Такие ситуации часто воз­никают при исследовании самой процедуры тестирова­ния — например, при сравнении эффективности различ-

ных инструкций, бланков для регистрации ответов и т. д. Это относится и к сравнению эффективности обра­щений о наборе добровольцев и т. д. Когда необходи­мо сохранить анонимность респондентов, удобнее дру­гих оказывается план 6. В таких случаях рандомизация достигается путем перетасовки материалов, подлежа­щих распределению среди респондентов.

Статистические модели для плана 6

Простейший способ обработки — это применение t-критерия. План 6, пожалуй, единственный, для которого он оптимален. Однако ковариационный анализ и фор­мирование блоков по таким исходным показателям ис­пытуемых (Underwood [129]), как успеваемость, оценки в тестах, профессия родителей и т. д., позволяют повы­сить мощность статистической процедуры примерно до того же уровня, что и при использовании предваритель­ного тестирования. Идентичность предварительного и итогового тестов несущественна. Часто это различные формы «одного и того же» теста, и, следовательно, они менее идентичны, чем буквальное повторение предвари­тельного теста. Точность возрастает с увеличением сте­пени ковариации, и, хотя она обычно выше для экви­валентных форм «одного и того же» теста, чем для «различных» тестов, это чисто количественное разли­чие, причем такой надежный комплексный показа­тель, как, скажем, средний балл успеваемости ученика, может оказаться лучше короткого предварительного тестирования. Отметим, однако, что использование сред­него баллав качестве итогового показателя обычно не­желательно из-за его вероятной нечувствительности к X в сравнении с показателями, имеющими более тесную связь с содержанием и временем тестирования.

Неважно, как трактовать этот план с предваритель­ным псевдотестированием — как план 6 или как план 4. Он обладает достоинствами плана 6, избавляя экспери­ментатора от проведения настоящего предварительного тестирования, от повторного применения идентичного или весьма сходного по содержанию необычного мате­риала (как при изучении изменений социальных уста­новок). По этим причинам оценка плана 6 в отношении реакции на эксперимент будет несколько выше, чем для

планов 4 и 5. В социальных науках в целом это преимущество еще важнее, чем в педагогических исследованиях.

Факторные планы

На концептуальной основе трех последних планов, особенно планов 4 и 6, добавляя к ним новые группы с новыми X, можно построить сложные факторные планы, типичные для фишеровской традиции. В обычном однофакторном дисперсионном анализе мы будем иметь несколько «уровней» воздействия (Х₁, Х₂, Х₃и т. д., а также, возможно, Х₀«без X»). Если отсутствие X считать одним из уровней («режимов») эксперимента Х₀, то в планах 4 и 6 будет по одной группе на каждый уровень. По плану 5 мы будем иметь две группы (прошедшую и не прошедшую предварительное тести­рование) для каждого режима, так что можно провести двухфакторный дисперсионный анализ. Нам неизвестно о применении более чем двухуровневых планов, анало­гичных плану 5.

Обычно, если интерес представляет влияние пред­варительного тестирования, применяется план 6, так как иначе требуется большое число групп. Очень часто используются две и более независимых эксперименталь­ных переменных, каждая из которых реализуется на нескольких «уровнях», для чего требуется ряд групп: Х_a1Х_b1, Х_a1Хь₂, Х_а1Хь₃… Х_а2 Хь₁и т. д.

Разработка соответствующих планов, сопровождае­мая попытками экономить, устраняя из них некото­рые из возможных перестановок из Х_а и Хь, породила пугающие тайны факторного планирования (рандо­мизированные блоки, расщепленные делянки, греко-ла­тинские квадраты, дробные реплики, смешивание и т. п.). В результате возникла пропасть между передо­выми и традиционными методами педагогического ис­следования. Мы надеемся перебросить мост через эту пропасть, сохраняя непрерывную связь с традиционны­ми методами и уповая на присущий каждому здравый смысл. По-видимому, большинство идей, необходи­мых для понимания планирования эксперимента, лег­че всего понять, если рассмотреть их на материале

планов с двумя экспериментальными режимами без до­полнительных усложнений. Вместе с тем полное изло­жение проблем традиционного характера позволит до­стичь понимания необходимости и роли современных подходов. Уже в связи с поисками наиболее эффектив­ного способа обработки результатов всеми признанного старого эксперимента по плану 4 мы познакомились с необходимостью ковариационного анализа, который пока почти не использовался в этих условиях. Точно так же при обсуждении плана 5, когда в связи с необ­ходимостью контроля за некоторыми факторами мы столкнулись с задачей двух режимов, мы отказались от t-критерия в пользу соответствующей модели диспер­сионного анализа.

Здесь мы не можем вдаваться в детали статистиче­ского анализа факторных планов или хотя бы привести их примеры. Элементарные аспекты этих методов с ориентацией на исследователей в области педагогики изложены Эдвардсом [33], Фергюсоном [36], Джонсо­ном и Джексоном [54] и Линдквистом [68]. Надо на­деяться, однако, что следующие несколько разделов по­зволят читателю составить себе известное представле­ние о некоторых возможностях и трудностях, связанных с обсуждаемыми в этой главе вопросами планирования эксперимента. Мы не станем рассматривать обычные соображения по поводу использования латинских квад­ратов и многих других неполных планов, где ради эко­номии в жертву приносится информация о факторных взаимодействиях. (Однако применение латинских квад­ратов взамен контрольных групп, когда невозможна рандомизация, будет рассмотрено ниже — см. квазиэкс­периментальный план 11.) Причина, по которой мы решили не обсуждать неполные планы, состоит в том, что подробная информация о взаимодействиях имеет прямое отношение к проблеме внешней валидности, осо­бенно в науке, где возникают трудности с воспроизве­дением результатов в разных условиях (см. Wilk, Kempthorne [132]). Мы хотели бы рассмотреть в этом разделе следующие понятия: взаимодействие, нестинг и перекрестная классификация, а также конечные, фикси­рованные, рандомизированные и смешанные факторные модели.

Взаимодействие

Выше мы уже пользовались этим понятием, надеясь на то, что неподготовленный читатель поймет его значение из контекста. Как и ранее, мы делаем упор на то, как взаимодействие может отразиться на возможности обобщения результатов эксперимента.

Посмотрим, как выглядят на графике (рис. 2) пять возможных исходов эксперимента с тремя уровнями воздействий Х_а и Х_b,которые мы обозначим А и В.(Здесь мы пользуемся лишь одним из ряда возможных двумерных представлений задачи, в которой фигуриру­ют три измерения А, В и О).На рис. 2а представлен случай, когда имеются значимые главные эффекты А и В,но отсутствует их взаимодействие. (Разумеется, происходит суммирование эффектов с максимумом для А₃ В₃, но без взаимодействия, ибо эффекты аддитивны.) Во всех остальных случаях имеется значимое взаимо­действие помимо или взамен главных эффектов А и В. Иначе говоря, характер эффекта А зависит от конкрет­ного значения В. В этом смысле взаимодействие пред­ставляет собой «правило специфичности эффекта» и, следовательно, имеет отношение к проблеме обобщения результатов.

Эффект взаимодействия, показанный на рис. 2г, хо­рошо иллюстрирует сказанное. Здесь отсутствует глав­ный эффект А (то есть, подсчитав средние значения О для каждого А по всем В, мы получим горизонтальную линию). Но когда В находится на уровне 1, увеличе­ние А приводит к снижению О, а когда В находится на уровне 3, увеличение А приводит к возрастанию О. Отметим, что, если бы экспериментатор менял только А, оставляя В постоянным на уровне 1, результаты, хотя и были бы внутренне валидными, подсказывали бы ошибочное обобщение на случаи В₂ и В₃. Использова­ние более чем одного фактора в плане позволяет про­вести изучение возможностей обобщения или внеш­ней валидности любого итогового утверждения о глав­ном эффекте А. Ограничение этих возможностей или специфичность эффектов обнаруживают себя при ста­тистическом анализе в виде значимого взаимодействия.

На рис. 2д изображена еще более крайняя ситуа­ция: ни А, ни В не имеют главного эффекта (нет об-

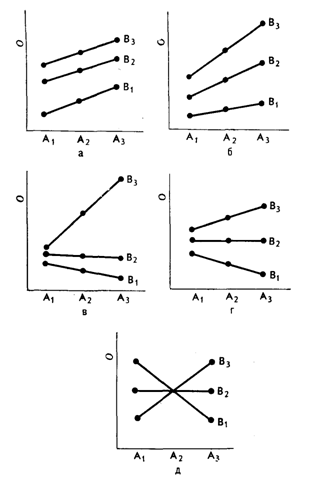
Р и с. 2. Некоторые возможные результаты факторного экспе­римента, проведенного по схеме 3×3.

щих правил, позволяющих судить, какой из двух уров­ней лучше), но наблюдается сильное и определенное взаимодействие между А и В. Рассмотрим гипотетиче­ский результат такого рода. Предположим, три типа учителей (например, склонные к спонтанной импрови­зации, к тщательной подготовке к уроку и полной опеке учеников) в целом работают одинаково эффективно.

Точно так же три метода обучения (например, групповая дискуссия, лекционный метод и индивидуальная работа с учениками) в целом обладают одинаковой эффективностью. В таком случае даже в отсутствие «главных эффектов» для типа учителя или метода обучения эти два фактора будут сильно взаимодействовать друг другом: импровизатор лучше проведет групповую дискуссию и хуже всего организует индивидуальную работу, тогда как сторонник опеки учеников продемонстрирует максимум эффективности, работая по индивидуальному методу, но плохо справится с проведением аскуссии.

Следует различать типы обнаруживаемых значимых ааимодействий. Тут нам, вероятно, поможет понятие «монотонность взаимодействия». Отметим, что в случаях, соответствующих рис. 2а и 2б, имеет место главный эффект и A, и B, причем главный эффект A направлен одну и ту же сторону для любого отдельного набора значений В. Таким образом, в новой ситуации мы с гораздо большей уверенностью можем ожидать увеличения O с ростом А, чем в случае 2, когда также могут иметь место значимые главные эффекты и значимое взаимодействие A и B. В случае 2б мы могли бы, соб­ственно говоря, быть почти так же уверены в общем характере главного эффекта А, как и в случае 2а, ко­гда взаимодействие отсутствует. Таким образом, выясняя возможность обобщения результатов, мы должны построить и детально изучить соответствующий график. Некоторые «монотонные», или однонаправленные, вза­имодействия почти или совсем не порождают ограниче­ний специфичности эффекта (см. Lubin [72], где при­водится широкое обсуждение данной проблемы).

Нестинг ¹

Во всех приведенных до сих пор примерах каждый из классификационных критериев (например, различные

_____________________________________________________________________________

¹ В контексте теории эксперимента нет точного русского экви­валента английского слова «nesting». Буквально его следует пони­мать как набор однородных объектов внутри более крупных еди­ниц (nests), наподобие, скажем, картотечных ящиков в секциях. Попытка перевести этот термин как «группировка» (см., например: X и к с Ч. Основные принципы планирования эксперимента. М., «Мир», 1967) представляется не вполне удачной, так как это слово весьма многозначно и не содержит указаний на специфический ха-

A и В) «перекрещивался» со всеми остальными крите­риями, то есть каждый уровень А фигурировал на всех уровнях В. Однако дисперсионный анализ не ограничи­вается только этой ситуацией.

До сих пор в роли критериев классификации у нас выступали экспериментальные воздействия. Но во мно­гих экспериментах могут быть использованы и другие признаки перекрестной классификации — например, пол или возраст учеников. Чтобы пояснить, в каких смыслах обычно употребляется термин «нестинг» применительно к классификации, нам придется обратиться к менее очевидным классификационным критериям.

Возьмем, к примеру, переменную «учитель». Пред­ставим себе эксперимент, в котором 10 учителей при­меняют два метода обучения данному предмету. В этом случае каждый отдельный учитель представляет собой конкретный «уровень». Полное перекрещивание пере­менной «учитель» с переменной «метод» будет иметь место, когда каждый учитель применяет оба метода в различных классах. Наличие «главного эффекта» фак­тора «учитель» свидетельствовало бы о том, что одни учителя работают лучше других, независимо от метода, который они используют. (Учащиеся или классы долж­ны выбираться в случайном порядке, иначе произойдет смешивание двух факторов — особенностей учителей и состава классов.) Значимое взаимодействие между пе­ременными «учитель» и «метод» означало бы, что для одних учителей более эффективен один метод, а для дру­гих — другой.

Предположим теперь, что, желая проследить далее такое взаимодействие, мы заинтересовались тем, кто из учителей — мужчины или женщины — работал лучше по данной методике. Разделив наших учителей на

__________________________________________________________________

рактер данной «группировки». Несколько более адекватным представляется использование в этой связи термина «иерархическая классификация». Однако и он является скорее формальным, нежели семантическим эквивалентом исходного термина, причем даже фор­мальная эквивалентность лишь приблизительна, ибо «nesting» соот­ветствует только двухуровневой иерархии. По-видимому, мы здесь сталкиваемся с тем редким случаем, когда иноязычный термин лучше не переводить, а просто дать в русской транскрипции. — Прим. перев.

5 мужчин и 5 женщин, мы приходим к «нестингу»: теперь переменная «учитель», хотя и полезная по-прежнему, не перекрещивается с переменной «пол», то есть один и тот же учитель не может принадлежать к тому идругому полу, в то время как «учитель» и «пол» пе­рекрещиваются с «методом». Такой нестинг требует несколько иного анализа данных, чем в том случае, когда все классификации перекрещиваются друг с дру-гом. (Соответствующие иллюстрации см. в: Green, Tukey [45], Stanley [111].) Кроме того, при нестинге ис­ключены некоторые взаимодействия переменных. Так, взаимодействия «учитель» — «пол» и «учитель» — «пол» — «метод» нельзя рассчитать, и в концептуаль­ном плане они не имеют смысла.

Распространим теперь данный эксперимент на не­сколько школ, так что «школа» становится переменной, главный эффект которой мог бы отражать различия в скорости усвоения материала учениками разных школ. В этих условиях, скорее всего, будет иметь место не­стинг учителей по школам, так как каждый учитель обычно ведет уроки только в одной школе. Хотя в этом случае возможно взаимодействие «учитель» — «школа», его можно рассчитать только в том случае, если все учителя работают одновременно во всех школах, охва­ченных экспериментом. Но тогда нестинг уступает место «перекрещиванию» этих признаков.

Учащихся, или испытуемых в эксперименте, также можно рассматривать как признак классификации (переменную). При полном перекрещивании каждый учащийся проходит через все режимы эксперимента. Но часто случается так, что ученики проходят лишь через некоторые, а не все режимы, то есть имеет место не­стинг. Такая ситуация часто возникает, например, при поэтапном изучении процесса научения. В этом случае можно получить кривые научения для каждого из ис­пытуемых, распределенных по двум способам обучения. Переменная «испытуемый» перекрещивается с «поряд­ковым номером пробы», но не со «способом обучения». Здесь мы можем изучать взаимодействие «испытуе­мый» — «номер пробы», но не «испытуемый» — «способ обучения». Точно так же нестинг возникнет в том слу­чае, когда ученики расклассифицированы по признаку пола.

Большинство переменных, представляющих интерес в педагогическом эксперименте, может взаимно пере­крещиваться, и нестинг для них не обязателен. Помимо уже названных случаев, исключение составляют: хро­нологический возраст, умственный возраст, школьный класс (первый, второй и т. д.) и социально-экономиче­ский уровень. Наблюдательный читатель, вероятно, уже заметил, что независимые переменные, или признаки классификации, бывают нескольких видов: 1) управля­емые переменные (например, метод обучения, выбира­емый по усмотрению экспериментатора); 2) потенци­ально управляемые переменные (например, школьные предметы, которые экспериментатор может выбирать случайным образом, но он редко пользуется этой воз­можностью); 3) относительно постоянные аспекты окру­жения (населенный пункт, школа, социально-экономи­ческий уровень), которые не находятся под непосред­ственным контролем экспериментатора, но которые в эксперименте служат четкими основами стратификации; 4) объективные («организмические») характеристики учеников (возраст, рост, вес, пол) и 5) характеристики учеников, проявляющиеся в их ответах (результаты различных тестов). Обычно первостепенный интерес представляют управляемые независимые переменные 1-го вида, хотя неуправляемые независимые переменные 3-го, 4-го и иногда 5-го вида служат повышению точ­ности и выяснению, насколько эффекты управляемых переменных поддаются обобщению. Переменные 5-го вида обычно фигурируют в качестве сопутствующих или зависимых от других показателей переменных. Другой способ рассмотрения независимых переменных — это учет присущей им упорядоченности (школьный класс, социально-экономический уровень, рост, номер пробы и т. д.) или неупорядоченности (методика, учебный пред­мет, учитель, пол и т. д.). Эффекты упорядоченных пе­ременных часто могут быть подвергнуты дальнейшему анализу для выяснения того, является ли тренд линей­ным, квадратичным, кубическим и т. д. (Grant [44], Myers [83]).