Логика и язык. Понятие логической формы и формальный язык логики

Язык – знаковая система, используемая для хранения и передачи информации в процессе коммуникации и познания действительности. Элементарные единицы языка – знаки. Знак – любой чувственно воспринимаемый предмет, воспроизводящий свойства, отношения другого предмета. По своему происхождению языки бывают естественные и искусственные. Естественный язык – это исторически сложившиеся в обществе информационные знаковые системы. Искусственный язык – это вспомогательная знаковая система, созданная на базе естественного языка для выполнения специальных задач. Язык логики является искусственным языком - это язык символов, формул, знаков, исчислений. Он отвлечен от конкретных особенностей слова и сосредоточен на его логической структуре, логической форме. Поэтому такой язык называется формализованным. Формализованными языками логики являются искусственные знаковые системы: язык логики предикатов и язык логики высказываний.

В языке логики используются следующие знаки:

1.Дескриптивные (описательные) символы:

а) имена(слово или словосочетание, обозначающее отдельный предмет или группу однородных предметов):

a, b, c, - символы для единичных имен предметов; предметные постоянные (константы);

x, y, z, ... - символы общих имен предметов; предметные переменные;

б) предикаторы(слова исловосочетания, обозначающие свойства и отношения предметов.)

P₁ , Q₁ , R₁ , ...; P₂ , Q₂ , R2 , ...; Pⁿ , Qⁿ , Rⁿ

в) высказывания (соединение слов, имеющее самостоятельный смысл, т.е. выражающее законченную мысль)

p, q, r .....- пропозиционные переменные;

2. Логические символы:

а) кванторы – символы для количественной характеристики высказываний:

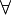- квантор общности, он символизирует выражения: все, каждый, всякий, всегда и т.п.

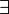- квантор существования, он символизирует выражения: некоторый, иногда, бывает, встречается, существует и т. п.;

б) логические связки:

Ú;+ - дизъюнкция (разделительное "или");

Ù;& - конъюнкция (соединительное "и");

®;É- импликация ("если..., то...");

«; ~ - эквивалентность (если и только если..., то...");

; ù - отрицание ("неверно, что...");

В логике язык важен, прежде всего, как основная форма выражения мыслей. Ключевой категорией в этой связи являются понятия логической формы, а именно выражение, фиксирующее ту часть содержания языкового контекста, которая остается в результате отвлечения от конкретных содержаний нелогических терминов или же от содержаний простых высказываний, входящих в данный контекст.

Другим фундаментальным понятием логики, непосредственно связанным с предыдущим – это понятие логического следования. Логическое следование представляет собой отношение между высказываниями по форме, которое есть соотношение по критерию истинности высказываний. Более развернуто и строго, это выражается в следующем определении:

Из множества логических форм каких-либо высказываний (посылки) логически следует другая логическая форма некоторого высказывания (заключение) тогда и только тогда, когда при любой интерпретации параметров в составе посылок и заключения, если все посылки принимают значение «истина», то и заключение также примет значение «истина».

2.3 Формально-логические законы - принципы мыслительной деятельности

Следует отличать понятие универсальное понимание научного закона как необходимой, существенной и повторяющейся связи между явлениями и процессами действительности от понимания логического закона. В специальном смысле под законом в логической теории понимается такая логическая форма высказывания, которая принимает значение «истина» при любой интерпретации параметров, входящих в ее состав.

В соответствии с ранее определенным предметом логики, понятие логического закона лежит в основе критериев правильности рассуждения, под которым понимается необходимое следование истинности одного суждения из истинности другого. В свою очередь, в основе понятия логического закона лежит понятие логического следования. Поэтому рассуждение, содержащее определенную связь между суждениями, будет называться правильным, если эта связь принимает характер логического следования или правильным можно назвать рассуждение, которое выражает логический закон.

Законов и правил в логике большое количество. Отметим лишь наиболее фундаментальные, по отношению, к которым остальные являются производными. Три из них сформулированы Аристотелем: закон (запрета) противоречия, закон тождества, закон исключенного третьего, четвертый - закон достаточного основания - выдвинут Г. Лейбницем.

Основные законы логики отражают фундаментальные свойства логической мысли - определенность, последовательность и обоснованность.

Закон тождества: мысли о предметах, свойствах или отношениях должны оставаться неизменными по содержанию в процессе всего рассуждения о них. В символической форме он записывается так: А = А.

Закон противоречия (непротиворечия):два несовместимых друг с другом суждения не могут быть одновременно истинными; по крайней мере одно из них необходимо ложно. В символической форме он выражается формулой ù (А ^ ù А).

Закон исключенного третьего:из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано. В символической форме записывается так: А v ùА.

Закон достаточного основания:всякая мысль истинна или ложна не сама по себе, а в силу достаточного основания.

В логических исчислениях законы мышления рассматриваются как тождественно-истинные высказывания, или логические тавтологии, которые являются истинными при любых значениях переменных

2.4 Понятие как форма мышления

Понятие – форма мышления, с помощью которой отображаются наиболее существенные, общие и отличительные признаки предметов, явлений, процессов.

Содержание понятия – это все признаки, с помощью которых оно определяется. Объем же составляют предметы, охваченные понятием. Закон обратного отношения между объемом и содержанием: чем богаче содержание, тем меньше объем и наоборот.

Виды понятий:

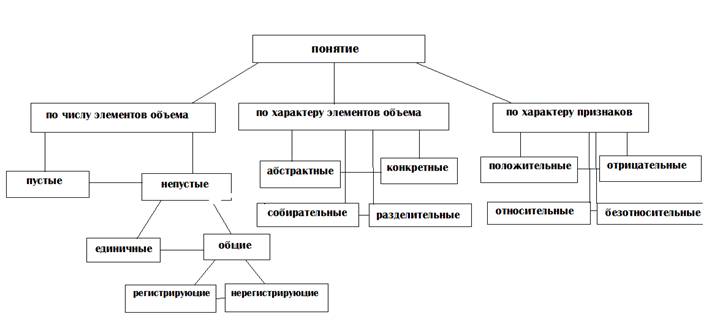
Логические отношения между понятиями бывают сравнимыми, если имеют в своем содержании общий признак, в противном случае понятия находятся в отношении несравнимости. Понятие, определенные как сравнимые, могут быть совместимыми или несовместимыми

Совместимыми являются понятия, имеющие общие элементы объема:

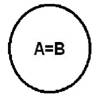
Равнозначные понятия имеют одинаковый объем, но разное содержание

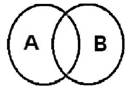Перекрещивающиеся понятия имеют разное содержание, а объемы их совпадают лишь частично.

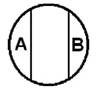
Понятия, находящиеся в отношении подчинения, имеют одинаковые элементы в содержании, а объем одного (подчиненного) полностью входит в объем другого (подчиняющего).

Несовместимыми являются понятия, не имеющие общих элементов объема:

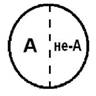
Противоречащими (контрадикторными) называются понятия, когда у одного из них имеется тот или иной признак, а у другого он отрицается

Противоположные (контрарные) понятия являются видами одного и

того же рода, но одно из них обладает каким-то признаком, а другое

имеет признак, несовместимый с данным.

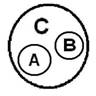
В отношении соподчинения (координации) понятия имеют в содержании общие элементы, благодаря которым все вместе входят в родовое понятие, но общих элементов в их объемах нет.

Операции с понятиями

Определение или дефиниция – это логическая операция, состоящая в придании точного смысла языковому выражению; это логическая операция, раскрывающая содержание понятия.

Цель определения – уточнить содержание используемых понятий. Задача определения – выделить систему признаков, общую и отличительную для предметов, обозначаемых термином.

Логическими элементами определения являются:

1) определяемое (дефиниендум) понятие – понятие, содержание которого требуется раскрыть;

2) определяющее (дефиниенс) понятие – понятие, раскрывающее содержание определяемого понятия.

Виды определений:

1. По функции, выполняемой в познании:

- номинальные – объясняют значения слова, имени, термина. Это предписания. Они не имеют истинностного значения;

- реальные – раскрывают сущность или отличительные особенности понятия. Это описательные высказывания. Являются истинными или ложными.

И реальные и номинальные определения могут быть как правильными, так и неправильными.

2. По форме:

- явные – раскрывают существенные признаки предмета. Основным видом явного определения является родовидовое определение. Родовидовые определения по характеру видового отличия подразделяются на несколько типов:

а) атрибутивно-реляционные. В них видовыми отличиями являются качества и свойства, присущие предметам самим по себе (атрибуты), а также отношения предметов к другим предметам (реляции);

б) генетические. В них указывается способ создания или путь возникновения того или иного явления;

в) операционное определение. В них признак указывает на действие (операцию), с помощью которого можно распознать определяемый предмет из рода;

г) определение через перечисление. В них в определяющей части просто перечисляются те предметы, которые подпадают под определяемое понятие;

д) определение через абстракцию. В них содержаться указания особого рода отношений (типа равенства). Такое равенство указывает на то, что предметы (будучи разными) обладают одинаковой величиной какой-то своей характеристики;

- неявные – определяемое и определяющее не имеют четких различий. К ним относят:

а) контекстуальные. В них не дается специально сформулированной дефиниции, но из сообщения, сделанного письменно или устно, становится ясно, что подлежит обсуждению;

б) индуктивные. Это специально-научные определения. Объем определяемого понятия задается перечислением разновидностей предметов, входящих в него. Эти определения позволяют из исходных объектов путем применения к ним определенных операций получать новые объекты;

в) рекурсивные. Это специально-научные определения, похожие на индуктивные, но в них задаются не классы предметов, а функции;

г) аксиоматические. Это специально-научные определения, в которых содержание терминов задается системой аксиом, куда входит определяемое понятие;

д) определение через указание на отношение предмета к своей противоположности.

Иногда используют приемы, сходные с определением. Среди таковых можно выделить остенсивные определения, объяснения, характеристики, описания, сравнения, различения. Остенсивное определение – это определение, устанавливающее значение термина путем демонстрации предмета, обозначаемого этим термином. Объяснение не столько заменяет определение того или иного явления, сколько дополняет его или делает его понятным. Это достигается за счет того, что незнакомые термины выражают через другие, известные.С помощью характеристики указывают на черты или особенности предмета, важные в каком-либо отношении. Задача описания наиболее точно и полно указать признаки предмета.

Правила определения понятий

1. Определение должно быть точным и ясным. Определение должно указывать на известные признаки, не нуждающиеся в определении. Иначе возникает ошибка, называемая определением неизвестного через неизвестное. Определение будет неясным, если определяющий термин – двусмысленный, метафорический, представлен сравнением. Оно не раскрывает сущности предмета.

2. Определение должно быть соразмерным. Слишком узкое определение, когда объем определяющего понятия уже, чем определяемого. Бывают также слишком широкие определения. В них определяющие понятия являются более емкими, чем определяемые. Могут быть определения, слишком широкие в одном отношении и слишком узкие в другом.

3. Определение не должно быть тавтологичным (не должно образовывать круга).

4. Определение не должно быть отрицательным.

Операция добавления новых признаков в содержание и перехода к более узким понятиям называется ограничением.

Операция отбрасывания от данного понятия некоторых признаков и перехода к более широким понятиям называется обобщением.

Деление понятия – логическая операция, раскрывающая объем понятия через перечисление его видов.

Различают следующие способы деление понятий:

1. Мереологическое деление – это членение понятия по типу «целое-часть».

2. Таксономическое деление предполагает членение по типу «род-вид».

Правила деления:

1. Деление должно быть соразмерным. Объем делимого понятия должен быть в точности равен сумме объемов членов деления.

2. Деление по одному основанию не должно перемежаться с делением по другому основанию.

3. Деление должно быть непрерывным и последовательным.

4. Члены деления должны исключать друг друга.

Суждение как форма мышления

Суждение – форма мышления, в которой посредством связи понятий утверждается или отрицается наличие признака предмета или отношения между предметами. Суждениевыражается повествовательным предложением и характеризуется как истинное или ложное.

Субъект (S)- это понятие, отображающее предмет, о котором идет речь. Предикат(P) выражает свойства, приписываемые предметам из объема понятия-субъекта или отрицаемые у них.Квантор служит для указания количественной характеристики суждения и выражается словами "все", "каждый", "всякий", "никакой", "некоторый", "большинство", "отчасти", "почти все" и пр. Связка задает качество суждения: когда свойство, отмечаемое в предикате, приписывается субъекту, оно утвердительное, когда же отмечается его отсутствие, - отрицательное. Связка обозначается словами "есть", "является", "представляет собой" и другими эквивалентными им выражениями.

Типы суждений

Суждения делятся на простые и сложные. Простым называется суждение, выражающее связь двух понятий. Суждение, состоящее их нескольких простых суждений, называется сложным.

Простые суждения

Выделяют следующие виды простых суждений:

1. суждения свойств (атрибутивные или категорические). В них указывается принадлежность (или не принадлежность) предметам тех или иных свойств.

По качеству категорические суждения делятся на:

- утвердительные. Выражают наличие какого-то признака;

- отрицательные. Выражают отсутствие признака;

По количеству категорические суждения делятся на:

- общие. Если понятие, стоящее на месте субъекта, берется во всем объеме;

- частные. В том случае, когда говорится о части объема понятия-субъекта;

- единичные. Если в качестве субъекта берется единичное понятие;

Исходя из объединенной классификации, все суждения делят на четыре вида и у каждого из них есть свое обозначение латинской буквой: общеутвердительные (А), общеотрицательные (Е), частноутвердительные (I), частноотрицательные (О);

2. суждения отношений, или релятивные. Их отличительная особенность состоит в том, что отмечаемое ими свойство нельзя отнести к одному объекту. Оно возникает из взаимодействия двух или нескольких объектов;

3. суждения существования (экзистенциальные). В них отмечается наличие (или отсутствие) в действительности тех или иных явлений.

Выделяющими называютсуждения, в которых только данному субъекту приписывается указанное свойство (Все (Некоторые) S, и только S, есть (не есть) P).

Исключающими называютсуждения, в которых отражается принадлежность (или непринадлежность) признака всем предметам, за исключением некоторой их части (Все S, если они не являются S1, есть (не есть) P).

Сложные суждения

Сложные суждения – суждения, состоящие из нескольких простых, связанных логическими связками.

Виды сложных суждений:

- соединительные (конъюнктивные)суждения состоят из нескольких простых, связанных логической связкой «и» (p^q). Коньюктивное суждение истинно при истинности всех его конъюнктов и ложно при ложности хотя бы одного;

- разделительные (дизъюнктивные)суждения состоят из нескольких простых, связанных логической связкой «или». Различают два типа разделительных суждений:

а) нестрогая дизъюнкция – суждения, в которых связка «или» употребляется в соединительно-разделительном значении (pÚq). Нестрогое дизъюнктивное суждение истинно при истинности хотя бы одного члена дизъюнкции и ложно при ложности обоих ее членов;

б) строгая дизъюнкция (исключающая) - суждения, в которых связка «или» употребляется в разделительном значении (или p, или q) (р q).

Дизъюнктивное суждение может быть полным (закрытым), если в суждении перечислены все признаки определенного рода; или неполным (открытым) если в суждении перечислены не все признаки определенного рода. Полная дизъюнкция в схемах обозначается так: <pÚqÚr>.

Строгое дизъюнктивное суждение истинно при истинности одного и ложности другого члена дизъюнкции. Оно ложно, если оба члена истины или ложны;

- условные (импликативные)суждения состоят из нескольких простых, связанных логической связкой «если…, то…» (р®q). Импликативное суждение ложно при истинности предпосылки (р) и ложности заключения (q). В других случаях оно истинно;

- эквивалентные (двойная импликация)суждения включают два суждения, связанные двойной условной зависимостью, выражаемой связкой «если и только если…, то…» (р«q). Эквивалентное суждение истинно, когда оба суждения принимают одинаковые значения.

Таблица1 - Таблица истинности суждений

Логические переменные	Логические операции
отрицание	конъюнкция	дизъюнкция	исключающая дизъюнкция	импликация	эквиваленция
p	q	p	p Ùq	pÚq	p q	p®q	p«q
и	и	л	и	и	л	и	и
и	л	л	л	и	и	л	л
л	и	и	л	и	и	и	л
л	л	и	л	л	л	и	и

В сложном логическом выражении следующий порядок выполнения логических операций: инверсия (отрицание) – конъюнкция – дизъюнкция –импликация - эквивалентность. Для изменения указанного порядка выполнения логических операций используются скобки.

Отношения между суждениями

Отношения между простыми суждениями:

1. Несравнимые суждения имеют различные субъекты и предикаты;

2. Сравнимые сужденияимеют один и тот же субъект и предикат. Их называют суждениями одинаковой материи. Они могут различаться между собой кванторами и связками. Между суждениями этого рода устанавливаются определенные твердые соотношения по их истинностным значениям, которые удобно изображать графически с помощью логического квадрата (Рисунок 1).

Сравнимые суждения разделяются на совместимые и несовместимые.

К совместимым относятся суждения, которые одновременно могут быть истинными. Различают три вида совместимости:

- эквивалентность (полная совместимость). Эквивалентными являются такие суждения, которые имеют одинаковые логические характеристики: одинаковые субъекты и предикаты, однотипную — утвердительную или отрицательную — связку, одну и ту же выраженную квантором количественную характеристику. С помощью логического квадрата отношения между простыми эквивалентными суждениями не иллюстрируются. Эти суждения принимают одни и те же значения истинности;

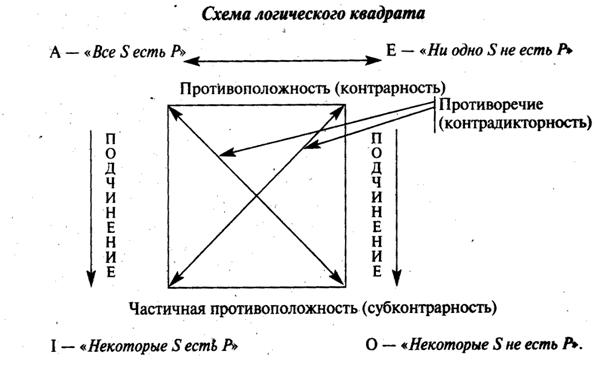
Рисунок 1

- частичная совместимость (субконтрарность). Частичная совместимость характерна для суждений I и О, которые могут быть одновременно истинными, но не могут быть одновременно ложными;

- подчинение. Подчинение имеет место между суждениями А и I, E и О. Для них характерны следующие две зависимости: при истинности общего суждения частное всегда будет истинным, и, при ложности частного суждения общее суждение также будет ложным.

Несовместимыми являются суждения, которые одновременно не могут быть истинными. Различают два вида несовместимости:

- противоположность (контрарность). Противоположными являются суждения А и Е, которые одновременно не могут быть истинными, но могут быть одновременно ложными;

- противоречие (контрадикторность). Противоречащими являются суждения А и О, Е и I, которые одновременно не могут быть ни истинными, ни ложными.

Отношения между сложными суждениями

Сложные суждения также могут быть сравнимыми и несравнимыми.

1. Несравнимые — это суждения, которые не имеют общих пропозиционных переменных.

2. Сравнимые — это суждения, которые имеют одинаковые пропозиционные переменные (составляющие) и различаются логическими связками, включая отрицание.

Сложные сравнимые суждения могут быть совместимыми и несовместимыми.

Совместимые суждения могут быть одновременно истинными. Как и в случае простых суждений, различают три вида совместимости сложных суждений:

- эквивалентность. Эквивалентные— это суждения, которые принимают одни и те значения истинности. Существует четыре основные эквивалентности:

1) выражение конъюнкции через дизъюнкцию

ù(A^B) = ùA v ùB;

2) выражение дизъюнкции через конъюнкцию

ù (A v B) = ùA ^ ùB;

3) выражение импликации через конъюнкцию

A ® B =ù (A ^ ùB);

4) выражение импликации через дизъюнкцию

A ® B = ù A v B;

- частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными;

- подчинение. Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующего все виды рассуждений.

Несовместимыми являются суждения, которые одновременно не могут быть истинными.

- противоположность — отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными;

- противоречие — отношение между суждениями, которые одновременно не могут быть ни истинными, ни ложными. Чтобы получить сложное суждение, противоречащее исходному, последнее нужно подвергнуть отрицанию.

2.6 Логическое исчисление как тип формальной теории^٭

Понятие содержательной и формальной теории: в содержательных теориях исходные утверждения (посылки) рассуждения представляют собой некоторые допущения, а дедукция используется лишь для связи некоторых отдельных положений теории. Заключение при этом интерпретируется как условно истинное, т. е. зависит от истинности посылок (школьная арифметика, теория эволюции Дарвина, а также сама логика высказываний и логика предикатов). В формальных теориях оформляется (структурируется) не только само знание, но и средства его получения – логические законы и способы дедуктивного рассуждения.

Исчисление: формальная теория, в которой содержание фиксируется на специально созданном символическом языке, а все рассуждения в рамках этой теории строятся как преобразования одних последовательностей символов в другие их последовательности (формальные теории множеств, формальная арифметика, логическое исчисление).

Формальное рассуждение – выведение одних формул из других формул. Формальное рассуждение можно трактовать как модель (форму) различных содержательных рассуждений, имеющих ту же самую логическую структуру, т.е. формулы исчислений представляют собой логические формы высказываний.

Натуральное логическое исчисление: содержит только правило вывода и не содержит аксиом.

Если в содержательных логических теориях под логическим законом понимается общезначимая формула (формула принимающая значение «истина» при любых интерпретациях нелогических символов), а критерием правильности умозаключения является наличие семантического отношения логического следования между его посылками и заключением, то в логических исчислениях осуществляется попытка формализации данных понятий. С это целью вводятся синтаксические аналоги понятия «общезначимой формулы» (понятия теоремы) и отношения логического следования (отношение выводимости). Из множества формул (посылок) логически следует другая формула (заключение) тогда и только тогда, когда при любой интерпретации параметров в составе посылок и заключения, при которой все выражения из посылок принимают значение «истина», выражение заключения также примет значение «истина».

Правила вывода натурального исчисления*

1) &_{в (введение конъюнкции)} 5) &_{и (исключение конъюнкции)}

А , В А & ВА & В

А & В А В

2) v_{в (введение дизъюнкции)} 6) v_{и (исключение дизъюнкции – tollendo ponens)}

А__ _А__ А v В, А_

А v В А v В В

3) →_{в (введение импликации)} 7) →_{и (исключение импликации – modus ponens)}

__В___ А → В, А

С → В , где С- посл. Пос. В

4) _{В (введение отрицания)} 8) _{и (введение отрицания)}

В, ВА

С, где С – посл. Пос. А

Правило 3) → _{в (введение импликации)} 4) _{В (введение отрицания).} Своеобразие этих правил состоит в том, что формула Св заключениях этих правил – не любое выражение, а последнее допущение (посылка) в некотором рассуждении. Т.о., формулировка этих правил соотносит их с тем рассуждением, которое будет строиться.

Правило 3) позволяет по любой формуле В,содержащейся в рассуждении, перейти к импликации вида С→В,где С – последнее допущение, а на место консеквента, помещается формула В.

Правило 4) _в двухпосылочно и позволяет при обнаружении в рассуждении двух формул, противоречащих друг другу, В и В – перейти к формуле С, которая является отрицанием последнего допущения, если таковым была формула С, т.е. разрешает строящееся рассуждение вводить отрицание последней посылки.

При применении любого из правил необходимо иметь в виду, что логические константы, указанные в правилах, являются всегда главными знаками формул. К ним и только к ним (и ничему иному) могут применяться правила.

Вывод и доказательство в натуральном исчислении^٭

Выводом называется непустая конечная линейно упорядоченная последовательность формул С1, С2,….Сk., удовлетворяющая условиям:

(1) каждая Сi есть либо посылка, либо получена из предыдущих формул по одному из правил вывода;

(2) если в выводе применялись правила →в или в, то все формулы, начиная с последней посылки и вплоть до результата применения данного правила, исключаются из участия в дальнейших шагах вывода.

Последнее свойство (свойство исключенности некоторых формул из участия в дальнейшем построении вывода) означает, что эти формулы как бы «замораживаются» и изолируются в выводе (исключенные формулы), а посылка, которая при этом попадает в число исключенных формул – исключенная посылка.

Если дан вывод С1, С2,….Сk.,т.е. дана линейная последовательность формул, по условиям (1) и (2), и если неисключенными посылками являются формулы А1, А2,….Аnи последняя формула последовательностиСkграфически совпадает с формулой В, т.е. является формулой В, то про данную последовательность говорят, что она является выводом формулы Виз посылок А1, А2,….Аn. Этот факт обозначается посредством записи А1, А2,….Аn ├ В(«из посылок А1, А2,….АnвыводимоВ»),где « ˫ » - метазнак выводимости.

Если множество формул Г содержит (кроме всего прочего) каждую из неисключенных посылок А1, А2,….Аn, то в логике принято считать, что рассмотренная выше последовательноть С1, С2,….Сk.,является также и выводом формулы В из множества формул Г: Г ├ В.

Доказательство есть вывод из пустого множества неисключенных посылок. Последняя формула в доказательстве называется доказуемой формулой, или теоремой. Например, запись├ Вчитается: «В – теорема».

Под анализом вывода имеется в виду указание того, на каком основании та или иная формула появилась в выводе. Согласно определению вывода, таких оснований может быть только два: либо формула является посылкой, либо она получена из предыдущих по некоторому правилу вывода

2.7 Умозаключение

Умозаключение - это форма мышления, позволяющая из одного или нескольких суждений, называемых посылками, извлекать с помощью правил логики новое суждение - заключение.

Виды умозаключений

Всю совокупность известных логике умозаключений принято классифицировать по следующим основаниям:

1) по строгости правил вывода:

a) демонстративные (необходимые) - те, у которых заключение с необходимостью следуют из посылок, т.е. представляет собой логический закон;

b) недемонстративные (правдоподобные) – те, у которых правила вывода обеспечивают лишь вероятное следование заключения из посылок.

2) по направлению движения мысли:

a) дедуктивные, в которых мышление движется от общих положений к частным выводам. Они в свою очередь по числу посылок делятся на:

-непосредственные умозаключениями, у которых всего одна посылка.Они относятся к наиболее простым их разновидностям. В них происходит простая смена логической формы того или иного высказывания, содержание же остается неизменным;

- опосредствованные, у которых посылок более одной. Они сложнее и многообразнее первых;

b) индуктивные, делающие обобщения из частных наблюдений;

c) умозаключения по аналогии, т.е. от частного знания к частному. К ним, относятся и некоторые суждения с отношениями; иногда последнюю группу объединяют под названием традуктивные умозаключения.

Дедуктивные умозаключения