Тема: Исследование процесса формирования оптимальной стратегии решения задачи (Методика «Ханойская башня»)

Цель:исследование процесса формирования оптимальной стратегии и выработки определенных эвристических правил.

Вводные замечания.

Изучение процесса формирования оптимальных мыслительных стратегий является методически сложным. Традиционные методики исследования типа «рассуждение вслух» не позволяют объективно оценить структурные особенности протекания мыслительных процессов. Вместе с тем известно, что при решении новых задач человек пользуется приемами, которые сокращают и упрощают сам процесс решения. Одним из таких приемов является поиск и использование эвристических правил решений, которые существенно сокращают затраты времени и повышают вероятность решения задач. В качестве эвристических правил чаще всего оказываются логические операции, не всегда поддающиеся словесному описанию. Поэтому наиболее адекватной методикой, позволяющей производить анализ процесса формирования стратегии и выработки определенных эвристических правил, будет такая, которая позволит объективно фиксировать действия испытуемого, не требуя от него вербализации. Среди множества задач, которые можно использовать для этой цели, задача, называемая «Ханойская башня», считается наиболее удобной, так как все действия испытуемого при ее решении легко поддаются точной регистрации. Задача «Ханойская башня» была известна еще в древней Индии, а позднее привлекла внимание математиков благодаря возможности ее формализации. В качестве экспериментально-психологической данная задача впервые была использована в ГДР Ф. Кликсом и его сотрудниками для исследования роли эвристик в процессе решения задач.

Стимульный материал и оборудование.

Игровое поле (рис. 2), пирамида из шести дисков разного диаметра.

Бланк протокола, ручка.

Ход работы.

Все студенты учебной группы делятся на пары: экспериментатор и испытуемый. В задаче «Ханойская башня» от испытуемого требуется поэлементно перенести «башню» с клетки А на клетку С, придерживаясь определенных правил.

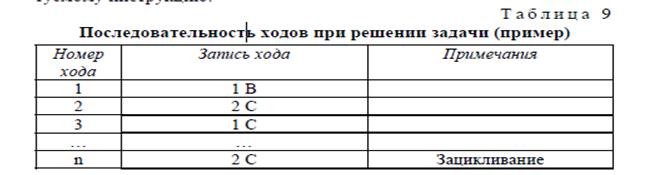
Для проведения исследования используется шесть дисков разного диаметра. Всем дискам присвоены порядковые номера от 1 до 6 в соответствии с размером – от меньшего (1) к большему (6). Они сложены в виде пирамидки. 7 диск является основанием башни и не используется в задании. Игровое поле представляет собой три расположенных в ряд участка, обозначенных слева направо как А, В и С. Все ходы испытуемого, т. е. любое перемещение каждого из дисков башни, заносятся в протокол (табл. 9). Положение диска после каждого перемещения по игровому полю записывают с помощью принятых номеров дисков и буквенных обозначений квадратов поля. До начала опыта экспериментатор устанавливает на поле А башню дисков и дает испытуемому инструкцию.

Инструкция испытуемому.

«Ваша задача состоит в том, чтобы, используя минимальное число ходов, поэлементно перенести башню, состоящую из шести дисков с участка А на участок С. Перемещать диски разрешается в любом направлении в пределах игрового поля! При решении этой задачи необходимо строго следовать следующим ограничивающим правилам:

1) одновременно нельзя перемещать два или более дисков;

2) перемещению подлежит только диск, лежащий сверху башни;

3) нельзя диск большего размера класть сверху диска меньшего размера;

4) при двукратном перемещении одного и того же диска Вам придется начать все сначала».

Обработка результатов.

При соблюдении указанных в инструкции правил последний ход испытуемого должен быть 1С.

Задача состоит в выявлении ошибок, допущенных испытуемым путем проверки последовательности его ходов. При этом следует обратить особое внимание на 32-й ход: если испытуемый усвоил эвристические правила решения задачи, то на этом ходу в протоколе должна быть запись «6C». Таким образом, перед 32-м ходом испытуемый должен понять, что для достижения цели башня из пяти дисков должна находиться на участке В. Это, в свою очередь, возможно, если башня из четырех дисков перед этим была на участке С и т. д. Внимание следует обращать и на ошибки типа «зацикливания», т. е. многократное повторение одних и тех же ходов, не ведущих к решению задачи. Задача имеет единственное оптимальное решение: она решается за 63 хода, что может быть выражено как 2n–1, где п – число дисков в башне.

В анализе необходимо указать, на какой по счету попытке испытуемый усвоил эвристические правила решения данной задачи и какие ошибки и вследствие каких причин он допускал. Кроме того, необходимо описать особенности процесса формирования оптимальной стратегии и выработки определенных эвристических правил у конкретного испытуемого.

Контрольные вопросы:

1. Существует ли зависимость между первым ходом (перемещением первого диска) и оптимальной стратегией решения задачи?

2. Какая зависимость существует между числом дисков башни и минимальным числом ходов для перемещения башни с поля А на поле С?

3. Сформулируйте общее правило решения задачи типа «Ханойская башня».

Лабораторная работа № 12