Краткая классификация задач и методов их статистического решения
| Задачи | Условия | Методы |
| 1. Выявление различий в уровне исследуемого признака | а) 2 выборки испытуемых | критерий Макнамары Q критерий Розенбаума U критерий Манна-Уитни 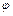 критерий (угловое преобразование Фишера) критерий (угловое преобразование Фишера) |
| б) 3 и больше выборок испытуемых | S критерий Джонкира H критерий Крускала-Уоллиса | |
| 2. Оценка сдвига значений исследуемого признака | а) 2 замера на одной и той же выборке испытуемых | T критерий Вилкоксона G критерий знаков 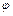 критерий (угловое преобразование Фишера) t- критерий Стьюдента критерий (угловое преобразование Фишера) t- критерий Стьюдента |
| б) 3 и более замеров на одной и той же выборке испытуемых | 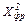 критерий Фридмана L критерий тенденций Пейджа t- критерий Стьюдента критерий Фридмана L критерий тенденций Пейджа t- критерий Стьюдента | |
| 3. Выявление различий в распределении признака | а) при сопоставлении эмпирического распределения с теоретическим | 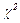 критерий Пирсона критерий Пирсона 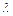 - критерий Колмогорова-Смирнова t- критерий Стьюдента - критерий Колмогорова-Смирнова t- критерий Стьюдента |
| б) при сопоставлении двух эмпирических распределений | 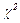 критерий Пирсона критерий Пирсона 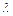 - критерий Колмогорова-Смирнова - критерий Колмогорова-Смирнова 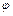 критерий (угловое преобразование Фишера) критерий (угловое преобразование Фишера) | |
| 4. Выявление степени согласованности изменений | а) двух признаков | 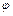 коэффициент корреляции Пирсона коэффициент корреляции Пирсона 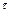 коэффициент корреляции Кендалла R – бисериальный коэффициент корреляции коэффициент корреляции Кендалла R – бисериальный коэффициент корреляции 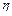 корреляционное отношение Пирсона корреляционное отношение Пирсона |
| б) трех или большего числа признаков | p коэффициент ранговой корреляции Спирмена r коэффициент корреляции Пирсона Линейная и криволинейная регрессии | |
| 5. Анализ изменений признака под влиянием контролируемых условий | а) под влиянием одного фактора | S критерий Джонкира L критерий тенденций Пейджа Однофакторный дисперсионный анализ Критерий Линка и Уоллеса Критерий Немени Множественное сравнение независимых выборок |
| б) под влиянием двух факторов одновременно | Двухфакторный дисперсионный анализ |
Работать с данной таблицей рекомендуется следующим образом:
1. По первому столбцу таблицы, выбирается задача, стоящая в исследовании.
2. По второму столбцу таблицы определяются условия решения задачи, например, сколько выборок обследовано или на какое количество групп может быть разбита обследованная выборка.
3. Выбирается соответствующий статистический метод. Можно выбрать несколько методов и сравнить их результаты.
Приложение 6
Таблицы критических значений
Таблица 14
Критические значения критерия T Вилкоксона
для уровней статистической значимостиP 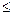 0,05 и P
0,05 и P 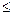 0,01
0,01
| n | P | n | P | ||
| 0,05 | 0,01 | 0,05 | 0,01 | ||
| - | |||||
| - | |||||
Таблица 15
Критические значения критерия U Вилкоксона-Манна-Уитни
для уровней статистической значимости P 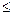 0,05 и P
0,05 и P 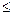 0,01
0,01
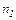 | |||||||||||||||||||
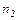 | P = 0,05 | ||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| P = 0,01 | |||||||||||||||||||
| - | - | ||||||||||||||||||
| - | - | ||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| P = 0,05 | |||||||||||||||||||
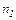 | |||||||||||||||||||
| P = 0,01 | |||||||||||||||||||
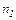 | |||||||||||||||||||
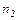 | P = 0,05 | ||||||||||||||||||
| P = 0,01 | |||||||||||||||||||
 | |||||||||||||||||||
 | P = 0,05 | ||||||||||||||||||
| P = 0,01 | |||||||||||||||||||
 | |||||||||||||||||||
 | P = 0,05 | ||||||||||||||||||
<Наши рекомендации
|
