Статистическая обработка результатов исследования
Применение методов математической статистики (статистических методов) для обработки результатов эмпирического исследования является обязательным требованием к курсовым и выпускным квалификационным работам по психологии и конфликтологии.
Методами статистической обработки результатов исследования называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе исследования, можно обобщать, приводить в систему, выявляя скрытые в них закономерности.
В зависимости от применяемых методов можно охарактеризовать выборочное распределение данных исследования, можем судить о динамики изменения отдельных показателей, о статистических связях существующих между исследуемыми переменными величинами.
Математическая обработка результатов исследования дает психологу возможность ответить на ряд вопросов:
1. Чем один человек отличается от другого (или группы лиц) по исследуемой психологической характеристике?
2. Чем отличается уровень развития одной психологической характеристики от другой у данной личности?
3. Как развиваются две группы лиц по какой-либо психологической характеристике и др.
Ответы на эти и другие вопросы могут быть получены в ходе психодиагностического обследования и зависят от правильного проведения этого обследования, а также от грамотной обработке и интерпретации полученных результатов.
Главная цель статистических методов - представить количественные данные в сжатой форме, с тем, чтобы облегчить их понимание.
Все методы статистического анализа условно делятся на первичные и вторичные.
Первичными называются методы, с помощью которых можно получить показатели, непосредственно отражающие результаты проводимых в эксперименте измерений. Под первичными статистическими показателями имеются в виду показатели, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов диагностики.
К первичным методам статистической обработки относят: определение среднего арифметического, дисперсии, моды и медианы.
Вторичными называют методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности.
К вторичным методам статистической обработки относят: корреляционный анализ, регрессионный анализ, факторный анализ, методы сравнения первичных данных двух или нескольких выборок.
Основные процедуры статистического анализа первичных результатов исследования
Меры центральной тенденции
Рассматривая методы математической статистики, применяемые для обработки данных тестовых исследований, можно выделить группу методов которые могут описывать те или иные меры центральной тенденции. Такие меры указывают наиболее типичный результат, характеризующий выполнение теста всей группой. Самая известная из таких мер – среднеарифметическое значение (М).
Среднеарифметическое (или выборочное среднее) значение представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута исследованию (выборка испытуемых). Сравнивая среднее значение двух или нескольких групп, мы можем судить об относительной степени развития у людей, составляющих эти группы, оцениваемого качества.
Среднеарифметическое определяется по следующей формуле:
М = 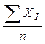

где М - среднеарифметическое значение
n - количество испытуемых
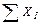 - сумма всех результатов
- сумма всех результатов
Пример: В исследовании объема вербальной механической памяти, тест «10 слов» в группе из 12 испытуемых (n = 12), получены следующие результаты (количество запомненных слов): 5, 4, 5, 6, 7, 3, 6, 2, 8, 6, 9, 7
Среднеарифметическое значение (М) 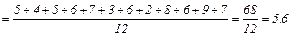
Для данной выборки среднеарифметическое значение (М) = 5,6
Другой мерой центральной тенденции является мода (Мо) - наиболее часто встречающийся результат. В интервальном частотном распределении мода определяется как середина интервала, для которого частота максимальна.
Пример: В ряду значений 2, 3, 4, 5, 5, 6, 6, 6, 7, 7, 8, 9 модой является 6, потому, что 6 встречается чаще любого другого числа.
Обратите внимание, что мода представляет собой наиболее часто встречающееся значение (в данном примере это 6), а не частоту встречаемости этого значения (в данном примере равную 3).
Когда два соседних значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений.
Пример: в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота больше, чем частота других значений 1 и 6 (у которых она равна 1). Следовательно, модой этого ряда будет величина 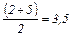
Третья мера центральной тенденции – медиана (Ме), - результат, находящийся в середине последовательности показателей, если их расположить в порядке возрастания или убывания. Справа и слева от медианы (Ме) в упорядоченном ряду остается по одинаковому количеству данных (50% и 50%). Если ряд включает в себя четное количество признаков, то медианой (Ме) будет среднее, взятое как полусумма двух центральных значений ряда.
Пример: Найдем медиану выборки: 5, 4, 5, 6, 7, 3, 6, 2, 8, 6, 9, 7.
Упорядочим выборку: 2, 3, 4, 5, 5, 6, / 6, 6, 7, 7, 8, 9. Поскольку здесь имеется четное число элементов, то существует две «середины» - 6 и 6. В этом случае медиана определяется как среднее арифметическое этих значений.
Ме 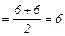
Пример: Найдем медиану выборки с нечетным количеством значений: 9, 3, 5, 8, 4, 11, 13.
Сначала упорядочим выборку по величинам входящих в нее значений. Получим: 3, 4, 5, 8, 9, 11, 13. Поскольку в выборке семь элементов, четвертый по порядку элемент будет серединой ряда. Таким образом, медианой будет четвертый элемент - 8
Значения Ме и Мо полезны для того, чтобы установить является ли распределение частных значений изучаемого признака симметричным и приближающимся к нормальному распределению. Среднее арифметическое (М), медиана (Ме) и мода (Мо) для нормального распределения обычно совпадают или очень мало отличаются друг от друга. При нормальном распределении результатов график распределения имеет форму колокола (рис. 2).
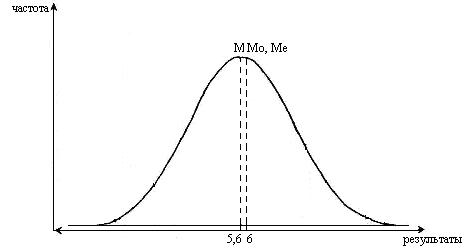
Рис. 2. График нормального распределения результатов исследования
Меры разброса данных
Для более полного описания результатов эмпирического исследования используются меры разброса данных, характеризующие степень индивидуальных отклонений от центральной тенденции. Это самый простой показатель, который можно получить для выборки - разность между максимальной и минимальной величинами данного конкретного вариационного ряда. Мера разброса данных позволяет сравнивать между собой разные группы. Чем сильней варьирует измеряемый признак, тем больше величина разброса данных и наоборот.
Необходимо отметить, что данная мера крайне неточна и неустойчива. Единственный необычно высокий или низкий результат может повлиять на величину размаха.
Более точный метод измерения разброса данных основан на учете разности между каждым индивидуальным результатом и среднеарифметическим значением по группе. Такой мерой разброса является дисперсия или средний квадрат отклонения ( 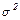 ).
).
Дисперсия характеризует насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонение или разброс данных. Дисперсия определяется по следующей формуле:
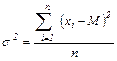
где 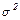 - дисперсия
- дисперсия
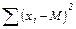 - выражение, означающее, что для всех значений x от первого до последнего в данной выборке вычисляется разность между частными и средними значениями, эти разности возводятся в квадрат и суммируются
- выражение, означающее, что для всех значений x от первого до последнего в данной выборке вычисляется разность между частными и средними значениями, эти разности возводятся в квадрат и суммируются
n - объем выборки
Вычислим дисперсию ( 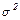 ) для следующего ряда: 2, 4, 6, 8, 10. Прежде всего, найдем среднее (М) для данного ряда, оно равно 6.
) для следующего ряда: 2, 4, 6, 8, 10. Прежде всего, найдем среднее (М) для данного ряда, оно равно 6.
Из каждого элемента ряда вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. Экспериментальные данные этой задаче, необходимые для расчета дисперсии, представим в виде (табл. 4)
Таблица 4
Первичный результат 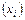 | 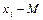 | 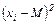 |
| - 4 | ||
| - 2 | ||
| М = 6 | 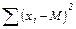 = 40 = 40 |
Далее разности возводят в квадрат суммируются. Полученную сумму квадратов разностей делим на объем данной выборки. В нашем примере получится следующее: 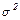
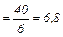
Общий алгоритм вычисления дисперсии ( 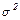 ) следующий:
) следующий:
1. Вычисляется среднее по выборке
2. Для каждого элемента выборки вычисляется его отклонение от среднего.
3. Каждый элемент множества возводят в квадрат.
4. Находится сумма этих квадратов.
5. Эта сумма делится на общее количество членов используемой выборки.
Очень часто вместо дисперсии для выявления разброса частных данных относительно средней используют производную от дисперсии величину, называемую стандартным отклонением. Стандартное отклонение равно квадратному корню, извлекаемому из дисперсии ( 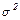 ), и обозначается тем же знаком, только без квадрата (
), и обозначается тем же знаком, только без квадрата ( 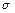 ). Эта величина в ряде случаев оказывается более удобной характеристикой варьирования, чем, дисперсия, так как выражается в тех же единицах, что и средняя арифметическая величина.
). Эта величина в ряде случаев оказывается более удобной характеристикой варьирования, чем, дисперсия, так как выражается в тех же единицах, что и средняя арифметическая величина.
В нашем примере 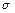
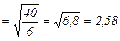
О чем же свидетельствует стандартное отклонение равное 2, 58? Оно позволяет сказать, что большая часть результатов данного исследования располагается в пределах 2, 58 от средней, т. е. между 3, 42 (6 – 2,58) и 8, 58 (6 + 2,58).
Для того чтобы лучше понять, что подразумевается под «большей частью результатов», необходимо рассмотреть те свойства стандартного отклонения, которые проявляются при нормальной или приблизительно нормальной кривой распределения, так как здесь существует прямое соответствие между 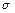 и относительным количеством случаев. На рис. 3 по горизонтальной оси отложены интервалы, соответствующие отклонению в 1
и относительным количеством случаев. На рис. 3 по горизонтальной оси отложены интервалы, соответствующие отклонению в 1 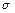 , 2
, 2 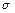 и 3
и 3 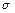 вправо и влево от среднего значения (М). Процент случаев, приходящийся на интервал М + 1
вправо и влево от среднего значения (М). Процент случаев, приходящийся на интервал М + 1 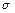 в нормальном распределении, равен 34, 13. Поскольку кривая симметрична, 34,13 случаев приходится также на интервалы от М - 1
в нормальном распределении, равен 34, 13. Поскольку кривая симметрична, 34,13 случаев приходится также на интервалы от М - 1 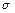 , так, что диапазон от - 1
, так, что диапазон от - 1 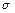 до + 1
до + 1 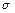 охватывает 68, 26 % случаев. Почти все случаи (99,72%), т. е. почти все показатели лежат в пределе от - 3
охватывает 68, 26 % случаев. Почти все случаи (99,72%), т. е. почти все показатели лежат в пределе от - 3 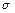 до + 3
до + 3 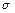 относительно среднего значения.
относительно среднего значения.
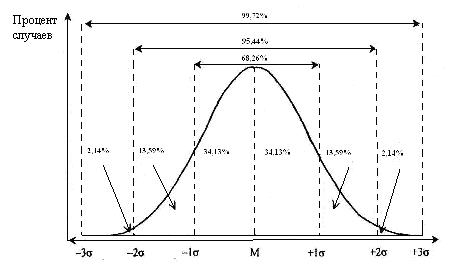
Рис. 3. Процентное соотношение случаев для кривой нормального распределения
Эта закономерность известна как закон «трех сигм» и является одной из характеристик нормального распределения.
