Логическая операция деления понятий. Структура деления понятий, виды деления. Правила деления, возможные ошибки при делении понятий.

Деление понятия - это логическая операция разбиение объёма исходного понятия на объёмы видовых понятий.

Логическая структура деления

1. Делимое понятие, т.е. родовое понятие, объем которого раскрывается посредством его деления на меньшие объемы.

2. Члены деления, т.е. видовые понятия, которые получаются в результате деления объема родового понятия.

3. Основание деления, т.е. признак, который образует виды предметов, обобщенных в делимом понятии.

Виды деления

• Деление по изменению видообразующего признака — деление объема понятия на подклассы (виды) по определенному признаку, называемому основанием деления.

• Дихотомическое деление — деление объема понятия на два подкласса (вида), обозначаемые двумя противоречащими друг другу понятиями. Таким образом, сущность дихотомического деления состоит в выделении двух противоречащих друг другу членов деления, объемы которых полностью исчерпывают объем делимого понятия.

Правила деления

1. Деление должно быть соразмерно. При делении по видообразующему признаку объединение членов деления должно совпадать с объемом делимого понятия.

2. Деление должно производиться только по одному основанию.

3. Члены деления должны исключать друг друга, т.е. элементы исходного понятия должны равняться объёму делимого понятия.

4. Правило непрерывности. Требует не делать скачков делений понятий, т.е. вче члены деления должны быть однопорядковыми видами.

Формализованный язык классической логики высказываний. Определение формулы и подформулы формулы. Таблицы истинности. Классификация формул по условиям истинности. Сокращенные таблицы истинности, их назначение.

Формализованный язык классической логики высказываний.

Формализованный язык классической логики предикатов является фрагментом и результатом некоторой реконструкции естественного языка. Специфика его состоит, прежде всего, в наличии точных правил построения высказываний (формул) и сложных имен (термов). Этот язык предназначен для аксиоматического построения теорий, для анализа содержания высказываний естественного языка и выявления логических отношений между ними, для описания правил рассуждения, построения выводов и доказательств и т.д.

Формальный язык логики высказыванияч состоит из выражений сдледующих групп:

1. Потенциального бесконечного списка элементарных высказываний (р_1…p_n, q₁…q_n и так далее)

2. Логической связки (константы)
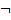- логическое отрицание («не» или «неверно, что»);
˄ - конъюнкция («и»);
v - дизъюнкция («или»);
Ú - строгая дизъюнкция («либо…, либо…»);
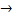- импликация («если…, то…»);
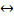- эквивалентность («тогда и только тогда, когда…»);

3. Технических связок. Скобки и запятая.
Формулами логики высказываний называются

1) атомарные формулы;

2) выражения вида (F) ˄ (G), (F) v (G), ⌐(F), (F)→(G), (F)↔(G), где F и G –

формулы логики высказываний.

Подформулой атомарной формулы является она сама. Подформулами формулы ⌐F являются формула ⌐F и все ее подформулы. Подформулами формул (F) ˄ (G), (F) v (G), (F) ↔G являются они сами и все подформулы формул F и G.

Таблицы истинности определяют условия истинности для сложных высказываний при условии, если элементы высказывания даны (предварительно) истинные значения.

2ⁿ – количество строк в таблице, где n – число различных высказываний.

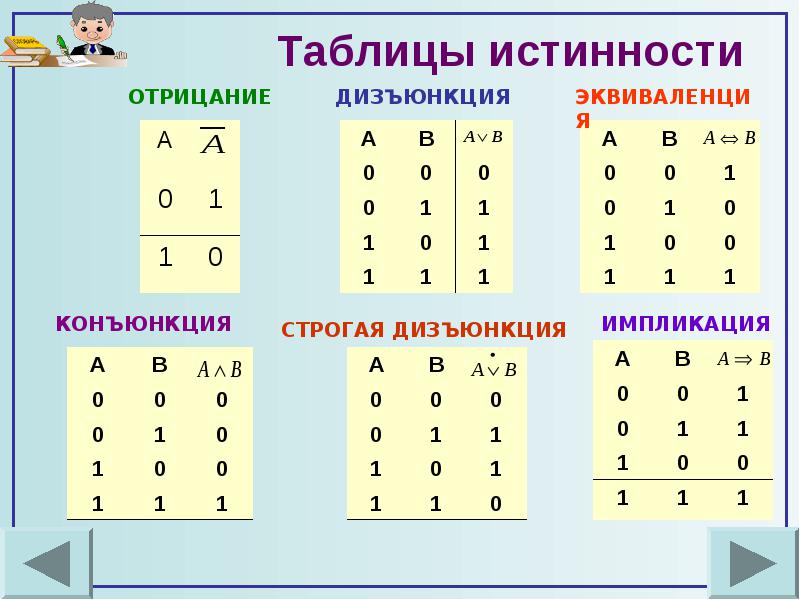
Классификация формул по условиям истинности.

Формула называется выполнимой, если некоторая ее конкретизация является истинным высказыванием
Формула называется тождественно истинной, если любая ее конкретизация является истинным высказыванием.
Формула называется опровержимой, если некоторая ее конкретизация является ложным высказыванием.
Формула называется тождественно ложной, если любая ее конкретизация является ложным высказыванием.
Для того чтобы определить, к какому типу относится формула, достаточно составить для нее таблицу истинности.

Сокращенные таблицы истинности, их назначение.
(Или сокращенный метод проверки общезначимости формул, или метод от противного)

1. Допустим, что формула не общезначима (т.е. в результате в столбце есть нуль).

2. Распределяем значения простых формул данной формулы.

3. Если встречаем противоречия (т.е. в одной и той же атомарной формуле принимается одновременно значение истинности 1 и ложности 0), то наше предположение, что формула необщезначима является неверным (т.е. формула общезначима)

4. Если противоречий нет, то наше предположение верно, формула необщезначима.