Проблема функции «Исключающего ИЛИ»

Один из самых пессимистических результатов М.Л. Минского гласит, что однослойный персептрон не может воспроизвести такую простую функцию, как «Исключающее ИЛИ». Это функция от двух аргументов, каждый из которых может быть нулем или единицей. Она принимает значение единицы, когда один из аргументов равен единице (но не оба). Проблему можно проиллюстрировать с помощью однослойной однонейронной системы с двумя входами, показанной на рисунке:

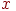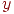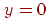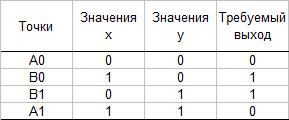
Обозначим один вход через , а другой через , тогда все их возможные комбинации будут состоять из четырех точек на плоскости , как показано на рисунке ниже. Например, точка и обозначена на рисунке как точка 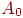. Таблица показывает требуемую связь между входами и выходом, где входные комбинации, которые должны давать нулевой выход, помечены 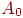и 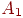, единичный выход - 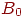и .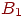

В сети на первом рисунке функция 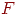является обычным порогом, так что OUT принимает значение 0, когда NET меньше 0,5, и 1 в случае, когда NET больше или равно 0,5. Нейрон выполняет следующее вычисление:

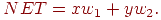(1)

Никакая комбинация значений двух весов не может дать соотношения между входом и выходом, задаваемого таблице. Чтобы понять это ограничение, зафиксируем 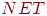на величине порога 0,5. Сеть в этом случае описывается уравнением (2). Это уравнение линейно по 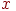и 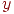, т. е. все значения по 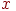и 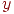, удовлетворяющие этому уравнению, будут лежать на некоторой прямой в плоскости .

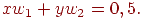(2)

Любые входные значения для 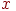и 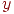на этой линии будут давать пороговое значение 0,5 для 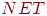. Входные значения с одной стороны прямой обеспечат значения 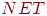больше порога, следовательно, 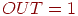. Входные значения по другую сторону прямой обеспечат значения NET меньше порога, делая 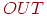равным 0. Изменения значений 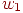, 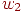и порога будут менять наклон и положение прямой. 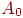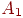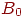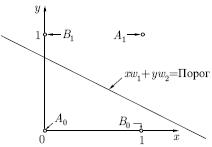Для того чтобы сеть реализовала функцию ИСКЛЮЧАЮЩЕЕ ИЛИ, заданную таблице, нужно расположить прямую так, чтобы точки , были с одной стороны прямой, а точки , 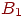— с другой. Попытавшись нарисовать такую прямую на втором рисунке, убеждаемся, что это невозможно. Это означает, что какие бы значения ни приписывались весам и порогу, сеть неспособна воспроизвести соотношение между входом и выходом, требуемое для представления функции ИСКЛЮЧАЮЩЕЕ ИЛИ. Взглянув на задачу с другой точки зрения, рассмотрим 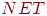как поверхность над плоскостью . Каждая точка этой поверхности находится над соответствующей точкой плоскости на расстоянии, равном значению 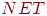в этой точке. Можно показать, что наклон этой 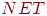-поверхности одинаков для всей поверхности . Все точки, в которых значение 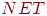равно величине порога, проектируются на линию уровня плоскости 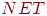(см. рисунок ниже).

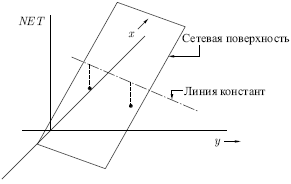
Ясно, что все точки по одну сторону пороговой прямой проецируются в значения 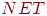большие порога, а точки по другую сторону дадут меньшие значения 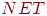. Таким образом, пороговая прямая разбивает плоскость на две области. Во всех точках по одну сторону пороговой прямой значение 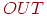равно единице, по другую сторону — нулю.

Карты Кохонена.

Самоорганизующиеся карты Кохонена – одна из разновидностей нейросетевых алгоритмов. Основные отличия данной технологии от остальных нейросетей является то, что обучение этой структуры происходит без учителя.

Нейросети данного типа применяются для решения различных задач начиная от прогнозирования до восстановления пропущенных данных. Алгоритм функционирования самообучающихся карт (Self Organizing Maps – SOM) представляет собой один из вариантов кластеризации многомерных векторов. Примером таких алгоритмов может служить алгоритм k-ближайших средних (c-means). Важным отличием алгоритма SOM является то, что в нем все нейроны (узлы, центры классов…) упорядочены в некоторую структуру (обычно двумерную сетку). При этом в ходе обучения модифицируется не только нейрон-победитель, но и его соседи, но в меньшей степени. За счет этого SOM можно считать одним из методов проецирования многомерного пространства в пространство с более низкой размерностью. При использовании этого алгоритма вектора, схожие в исходном пространстве, оказываются рядом и на полученной карте.

Структура

SOM подразумевает использование упорядоченной структуры нейронов. Обычно используются одно и двумерные сетки. При этом каждый нейрон представляет собой n-мерный вектор-столбец 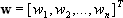, где n определяется размерностью исходного пространства (размерностью входных векторов). Применение одно и двумерных сеток связано с тем, что возникают проблемы при отображении пространственных структур большей размерности (при этом опять возникают проблемы с понижением размерности до двумерной, представимой на мониторе).

Обычно нейроны располагаются в узлах двумерной сетки с прямоугольными или шестиугольными ячейками. При этом, как было сказано выше, нейроны также взаимодействуют друг с другом. Величина этого взаимодействия определяется расстоянием между нейронами на карте. На рисунке 1 дан пример расстояния для шестиугольной и четырехугольной сеток.

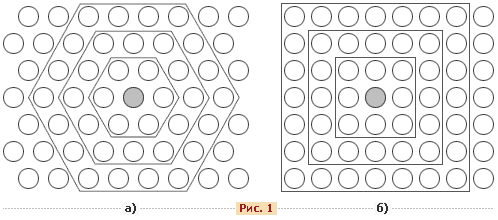
Расстояние между нейронами на карте для шестиугольной (а) и четырехугольной (б) сеток. При этом легко заметить, что для шестиугольной сетки расстояние между нейронами больше совпадает с евклидовым расстоянием, чем для четырехугольной сетки.

При этом количество нейронов в сетке определяет степень детализации результата работы алгоритма, и в конечном счете от этого зависит точность обобщающей способности карты.