Формализация эсихейрем с общими посылками

Эпихейремой в традиционной логике называется такой слож­носокращенный силлогизм, обе посылки которого представляют собой сокращенные простые категорические силлогизмы (энтимемы).

Схема эпихейремы, содержащей лишь общие и утвердитель­ные высказывания, обычно записывается следующим образом:

Все А суть С, так как А суть В.

Все D суть А. так как D суть Е.

______________________

Все D суть С.

Пример эпихейремы:

Благородный труд (А) заслуживает уважения (С), так как благородный труд (А) способствует прогрессу общества (В).

Труд учителя (D) есть благородный труд (А), так как труд учителя (D) заключается в обучении и воспитании подрастающего поколения (E).

_________________________________________

Труд учителя (D) заслуживает уважения (С).

Первая и вторая посылки эпихейремы представляют собой энтимемы, т, е. сокращенные категорические силлогизмы, у ко­торых одна из посылок опущена. Выразим полностью первую и вторую посылки эпихейремы.

1. Все В суть С. 2. Все Е суть А.

Все А суть В. Все D суть Е.

Все А суть С. Все D суть А.

Возьмем заключения первого и второго силлогизмов и сде­лаем их большей и меньшей посылками нового, третьего сил­логизма.

3. Все А суть С.

Все D суть А

._____________

Все D суть С.

Восстановим полностью эпихейрему.

1. Все, что способствует прогрессу общества (В), заслуживает уважения (С). Благородный труд (А) способствует прогрессу общества (В).

_____________________________________________________________________________________

Благородный труд (А) заслуживает уважения (С).

2. Обучение и воспитание подрастающего поколения (E) есть благородный труд (А).

Труд учителя (D) заключается в обучении и воспитании подрастающего по­коления (E).

__________________________________________________________________________________

Труд учителя (D) есть благородный труд (А).

Заключения первого и второго силлогизмов делаются посыл­ками третьего силлогизма.

3. Благородный труд (А) заслуживает уважения (С). Труд учителя (D) есть благородный труд (А).

_________________________________________________________________________________________________

Труд учителя (D) заслуживает уважения (С).

Приведем еще один пример эпихейремы.

Все рыбы (А) — позвоночные животные (С), так как рыбы (А) имеют скелет(В).

Все акулы (D) — рыбы (А), так как акулы (D) дышат жабрами (Е).

__________________________________________________________________________________________________________

Все акулы (D) — позвоночные животные (С).

В виде правила вывода восстановленную эпихейрему можно записать так:

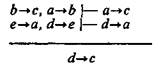
Это правило путем преобразований можно перевести в фор­мулу:

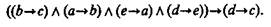
В целях большей наглядности переставим посылки и запишем эту формулу так:

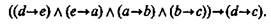
Можно доказать, что эта формула является законом логики. Так же как и энтимемы, сложносокращенные силлогизмы значительно упрощают наши рассуждения.

Выводы, основанные на логических связях между суждениями (выводы логики высказываний)

Если в логике предикатов простые суждения расчленялись на субъект и предикат, то в логике высказываний суждения не расчленяются, а рассматриваются как простые суждения, из ко­торых с помощью логических связок (логических постоянных) образуются сложные суждения.

Правила прямых выводов логики высказываний позволяют из данных истинных посылок выводить истинное заключение. На основе правил прямых выводов построены чисто условные и условно-категорические, разделительные и разделительно-категорические, а также условно-разделительные (лемматические) умозаключения.

УСЛОВНЫЕ УМОЗАКЛЮЧЕНИЯ

Чисто условным умозаключением называется такое опосред­ствованное умозаключение, в котором обе посылки являются условными суждениями. Условным называется суждение, име­ющее структуру: «Если а, то b». Структура его такая:

Если a, то b Схема:

Если b, то c a->b, b->c

____________ ______________

Если a, то c a->c

Согласно определению логического следствия, сформулиро­ванному в рамках исчисления высказываний, если а -> с есть логи­ческое следствие из данных посылок, то, соединив посылки зна­ком конъюнкции и присоединив к ним посредством знака имп­ликации заключение, мы должны получить формулу, которая является законом логики. Формула будет такова:

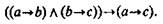
Доказательство тождественной истинности этой формулы мо­жно провести табличным методом. Этот вид умозаключения часто используется в школе, в частности на уроках математики, физики и др. Приведем пример.

Если по проводнику пропустить электрический ток, то вокруг проводника образу­ется магнитное поле.

Если вокруг проводника образуется магнитное поле, то железные опилки рас­полагаются в этом магнитном поле вдоль силовых линий.

___________________________________________________________________________________________________________________Если по проводнику пропустить электрический ток, то железные опилки рас­полагаются в его магнитном поле вдоль силовых линий.

В чисто условном умозаключении существуют его разновид­ности (модусы). К ним относится, например, такой:

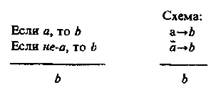
Формула: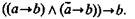

Формула является законом логики. В этом умозаключении суждение b истинно независимо от того, утверждается или от­рицается а.

Примером такого умозаключения является следующее рас­суждение:

Если будет хорошая погода, уберем урожай.

Если не будет хорошей погоды, уберем урожай.

______________________________

Уберем урожай.

Приведем пример из художественной литературы. Один из героев Агаты Кристи, оказавшийся на острове, рассуждает: «Генерал Макартур пребывал в мрачной задумчивости. Черт побе­ри, до чего все странно! Совсем не то, на что он рассчитывал... Будь хоть малейшая возможность, он бы под любым предлогом уехал... Ни минуты здесь не остался бы... Но моторка ушла. Так что хочешь не хочешь, а придется остаться».