Типы несовместимости: соподчинение, противоположность, противоречие

Соподчинение (координация) — это отношение между объема­ми двух или нескольких понятий, исключающих друг друга, но принадлежащих некоторому, более общему родовому понятию (например, «ель», «береза», «сосна» принадлежат объему понятия «дерево»). Они изображаются отдельными неперекрещивающимися кругами внутри более обширного круга. Это виды одного я того же рода.

В отношении противоположности (контрарности) находятся объемы таких двух понятий, которые являются видами одного и того же рода, и притом одно из них содержит какие-то призна­ки, а другое эти признаки не только отрицает, но и заменяет их другими, исключающими (т. е. противоположными признака­ми). Слова, выражающие противоположные понятия, являются антонимами. Антонимы широко используются в обучении. При­меры противоположных понятий: «храбрость» — «трусость»; «белая краска» — «черная краска». Объемы последних двух поня­тий разделены объемом некоторого третьего понятия, куда, например, входит «зеленая краска».

В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их ника­кими другими признаками. Если одно понятие обозначить А (на­пример, «высокий дом»), то другое понятие, находящееся с ним в отношении противоречия, следует обозначить не-А (т. е. «невы­сокий дом»). Круг Эйлера, выражающий объем таких понятий, делится на две части (А и не-А) и между ними не существует третьего понятия. Например, бумага может быть либо белой, либо небелой; человек бывает честным или нечестным; живо­тное — млекопитающим или немлекопитающим и т. д. Понятие А является положительным, а понятие не-А — отрицательным.

Понятия А и не-А также являются антонимами.

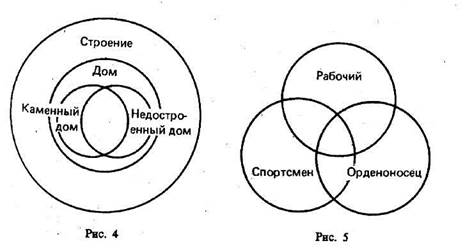
Примеры. Определить отношения между следующими поня­тиями; изобразить эти отношения кругами Эйлера (рис. 4, 5): 1. Дом, недостроенный дом, 2. Спортсмен, рабочий,

каменный дом, строение. орденоносец.

ОПРЕДЕЛЕНИЕ ПОНЯТИЙ

Определение (или дефиниция) понятия есть логическая опера­ция, которая раскрывает содержание понятия либо устанавливает значение термина.

С помощью определения понятий мы в явной форме указыва­ем на сущность отражаемых в понятии предметов, раскрываем содержание понятия и тем самым отличаем круг определяемых предметов от других предметов. Так, например, давая определе­ние понятия «трапеция», мы отличаем его от других четыреху­гольников, например от прямоугольника или ромба. «Трапе­ция — четырехугольник, у которого две стороны параллельны, а две другие — не параллельны» (1). Приведем еще несколько определений понятий, взятых из школьных учебников, которые принадлежат к двум различным видам определений. «Вещества, растворы которых проводят электрический ток, называются эле­ктролитами» (2). «Флорой называют видовой состав растений, произрастающих на той или иной территории» (3). «Естествен­ный отбор — процесс выживания наиболее приспособленных особей, который ведет к преимущественному повышению или понижению численности одних особей в популяции по сравнению с другими» (4).

В явном определении понятие, содержание которого надо раскрыть, называется определяемым понятием [definiendum (дефиниендум), сокращенно Dfd ], а то понятие, посредством которого оно определяется, называется определяющим понятием [definience (дефиниенс), сокращенно — Dfn ].

Реальные и номинальные определения

Если определяется понятие, то определение будет реальным. Если определяется термин, обозначающий понятие, то определе­ние будет номинальным. Из вышеприведенных определений (1) и (4)—это реальные определения, а (2) и (3) — номинальные

определения.

С помощью номинальных определений вводятся также новые термины, краткие имена взамен более сложных описаний пред­метов. Например, «навыком называют такое действие, в составе которого отдельные операции стали автоматизированными в ре­зультате упражнений».

Путем номинальных определений вводятся и знаки, заменя­ющие термины. Например, «Конъюнкция обозначается знаками ^ или & », «С — скорость света», «Тангенс угла α обозначается как tg α» и т. д.

В номинальном определении часто раскрывается и этимоло­гия того или иного термина. Например, «Термин «философия» происходит от греческих слов «филео» — люблю и «софия» — мудрость, что означает любовь к мудрости (или, как говорили раньше на Руси, любомудрие)».

Для номинальных определений характерно присутствие в их составе слова «называют(ся)». Номинальные определения часто встречаются в учебниках по математике для средней школы. Так, в курсе геометрии встречаются следующие номинальные опреде­ления: «Конус называется круговым, если основание его — круг» или «Круглый конус называют конусом вращения».

Определения делятся на явные и неявные. Явные определе­ния — это такие, в которых даны Dfd и Dfn и между ними устанавливается некоторое отношение равенства, эквивалентно­сти. Самое распространенное явное определение — определение через ближайший род и видовое отличие. В нем устанавливаются существенные признаки определяемого понятия.

Примеры. 1. «Правильный многоугольник — многоуголь­ник, у которого все стороны конгруэнтны и все углы равны».

2. «Барометр — прибор для измерения атмосферного давле­ния».

3. «Гротеск — один из способов сатирического изображения жизни, отличающийся резким преувеличением, сочетанием реаль­ного и фантастического».

Признак, указывающий на тот круг предметов, из числа кото­рых нужно выделить определяемое множество предметов, назы­вается родовым признаком, или родом. В приведенных примерах родовыми являются понятия «многоугольник», «прибор», «спо­соб сатирического изображения жизни».

Признаки, при помощи которых выделяется определяемое множество предметов из числа предметов, соответствующих ро­довому понятию, называются видовым отличием. При определе­нии понятия видовых признаков (отличий) может быть один или несколько.

К явным определениям понятий относятся и генетические определения. Они часто встречаются в школьных учебниках. Гене­тическим называется определение предмета путем указания на способ, которым образуется только данный предмет и никакой другой (это его видовое отличие). Генетическое определение яв­ляется разновидностью определения через род и видовое от­личие.

Приведем примеры генетических определений из области хи­мии. 1. Кислотами называются сложные вещества, образующие­ся из кислотных остатков и атомов водорода, способных заме­щаться атомами металлов или обмениваться на них. 2. Коррозия металлов — это окислительно-восстановительный процесс, обра­зующийся в результате окисления атомов металла и перехода их в ионы.