Операторы присваивания
Курсовая работа
По программированию и численным методам
На тему: Методы приближенного вычисления интеграла
Выполнил студент группы ТП-13-1
Попов Р.С.
Проверила: Давыдова А.В.
Днепропетровск
Содержание:
1. Постановка задачи.
2. Теоретические сведения.
3. Блок схема программы.
4. Текст программы.
5. Использованные операторы.
6. Результаты.
1.С помощью подпрограммы function вычисляем поочередно тремя способами приближенного вычисления значения интеграла F(x)= 
Интервал (1, 2)разбит на N частей. Ищем площадь для первого значения N=10, затем умножаем N на 2. Процесс продолжается до тех пор, пока относительная ошибка вычисления интеграла не станет меньше заданной точности, то есть пока ошибка не станет меньше ɛ = 0.0001.
2.1 Способ прямоугольников. Для вычисления интеграла 
делим отрезок 
на n равных частей точками
и обозначаем
  |
 |
 |
 |
 |
 |
 |
 |
 |
| y=f(x) |
| y |
| x |
| B |
 |
 |
 |
 |
 |
соответствующие значения функции
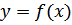. e
| А |
Полагаем приближенно, 
где
Это означает, что площадь каждой полоски, на которые разбивается криволинейная трапеция аABb, заменяется площадью прямоугольника с высотой 
и с основанием 
Сложив приближенные равенства для 
2.2 Способ трапеции.Как и в способе прямоугольников, делим отрезок 
y=f(x)  |
 |
| y |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| А |
| B |
Складывая приблеженные равенства для 
получаем формулу трапеции
2.3 Способ парабол (Симпсона).Разбиваем отрезок и на 2 N равных частей
точками и обозначим через
соответствующие значения функции 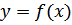. Рассматриваем двойной частичный отрезок 
и проводим дугу параболы через точку
Заменяем площадь каждой криволинейной плоскости 
, 
площадью соответствующей параболической полоски (полоски ограниченной сверху дугой параболы).
| A |
| B |
| y |
| x |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| |
 |
 |
 |
 |
 |
 |
 |
Тогда для приближенного вычисления площади всей криволинейной трапеции aABb получаем формулу
3.Метод прямоугольников
| function s(n) программы |
| i= 0, n-1 |
| y= (sqrt(x^2-0.16)/x sum=sum+y |
| s=h *sum sum=0 |
| Конец программы |
| a=1 b=2 |
| function s(n) программы |
| НЕТ |
| ДА |
| a=1; b=2 |
| i= 0, n |
| y= (sqrt(x^2-0.16)/x |
| Конец программы |
| i=n |
| f=x sum=sum+f |
Метод Симпсона
| Начало программы |
| N=10 S1=S(n) N=n*2 S2=S(n) |
 <0.001 |
| y= (sqrt(x^2-0.16)/x print *,'s=',s2, y |
| s1=s2 n=2*n s2=s(n) |
| ДА |
| НЕТ |
| Конец программы |
4. Метод прямоугольников
real s2
g=0.0001
k=0
n=10
s1=s(n)
n=2*n
s2=s(n)
1 if (abs(s1-s2)/s1 < g) then
print 4,s2
goto 3
else
k=k+1
s1=s2
n=2*n
s2=s(n)
goto 1
end if
3 print *, 'iter=',k
4 format (5x,'s=',F10.7)
end
function s(n)
a=1
b=2
h=(b-a)/n
do i=0,n-1
y=sqrt((a+i*h)**2-0.16)/(a+i*h)
sum=sum+y
end do
s=h*sum
sum=0
end
Метод трапеции
real s2
g=0.0001
k=0
n=10
s1=s(n)
n=2*n
s2=s(n)
1 if ((abs(s1-s2))/s1 < g) then
print 4,s2
goto 3
else
k=k+1
s1=s2
n=2*n
s2=s(n)
goto 1
end if
3 print *, 'iter=',k
4 format (5x,'s=',F10.7)
end
function s(n)
a=1
b=2
h=(b-a)/n
do i=0,n
y=sqrt((a+i*h)**2-0.16)/(a+i*h)
if ((i==0).or.(i==n)) then
f=y
goto 1
else
f=2*y
goto 1
end if
1 sum=sum+f
end do
s=(h/2) *sum
sum=0
end
4.Метод Симпсона
g=0.0001
k=0
n=10
s1=s(n)
n=2*n
s2=s(n)
1 if ( abs((s1-s2)/s1)<g ) then
print 4,s2
goto 3
else
k=k+1
s1=s2
n=2*n
s2=s(n)
goto 1
end if
3 print *, 'iter=',k
4 format (5x,'s=',F10.7)
end
function s(n)
a=1
b=2
h=(b-a)/n
do i=0,n
y=sqrt((a+i*h)**2-0.16)/(a+i*h)
if ((i==0).or.(i==n)) then
f=y
goto 2
end if
if (mod (i,2)==0) then
f=2*y
goto 2
else
f=4*y
goto 2
end if
2 sum=sum+f
end do
s=(h/3)*sum
end
Оператор END
Каждый программный модуль должен заканчиваться рядком END, который показывает транслятору конец модуля.
Вводо-вывод данных
Общая форма операторов READ, PRINT под руководительством списка
READ*, список
PRINT*, список
Список - список переменных в котором имя каждой переменной отделено от следующего имени запятой. Каждый оператор READ начинает чтение с новой записи данных, даже если в предыдущей записи остались считанные данные. Каждый оператор PRINT начинает печать с новой строки.
Операторы присваивания
Используются для определения значений переменной любого типа элементу массива или подстроки. Это один из наиболее часто используемых операторов в инженерных программах. Существует арифметический, логический и текстовый операторы присваивания. Общая форма оператора присваивания:
A=E
где A - идентификатор переменной, элемент массива или подстрока; E - арифметическое, логическое или текстовое выражение. Выполнение оператора состоит из трех этапов: Вычисляется правая часть, т.е. получается значение арифметического, логического или текстового типа. Если тип полученного значения отличен от типа идентификатора A, то производится перевод полученного значения в тип идентификатора A. Окончательно полученное значение заносится в ячейки памяти, отведенные компилятором для идентификатора A. Для логического оператора присваивания шаг 2) опускается, т.к. правая часть E обязана принимать логическое значение TRUE или FALSE.