Определение переменных Fuzzy Input, Output
Процесс разработки нечёткой экспертной системы в пакете CubiCalc начинается с определения переменных, которые будут использоваться в проекте project→variables→new.
Объявляем первую переменную 
как prohod (проходимость), зададим атрибуты переменной: выберем её тип (Fuzzy Input), зададим диапазон изменения её значений [0;60000], а также зададим начальное значение Initial Value равное 10000 (рис.1).
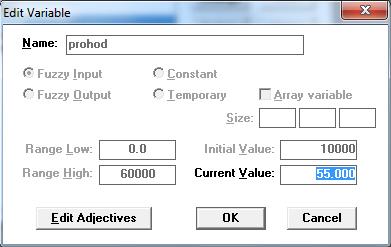
Рис.2
Объявляем вторую переменную 
как rast (расстояние до базы, задаём атрибуты переменной: выберем её тип (Fuzzy Input), зададим диапазон изменения её значений [0;40], а также зададим начальное значение Initial Value равное 0 (рис.3).
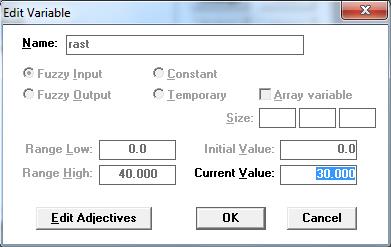
Рис.3
Объявляем третью (выходную) переменную Ранг как rate, задаём атрибуты переменной: выберем её тип (Fuzzy Output), зададим диапазон изменения её значений [0;1], а также зададим начальное значение Initial Value равное 0 (рис.4).
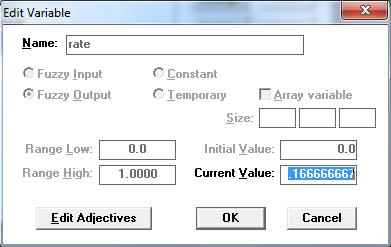
Рис.4
Построение функций принадлежности
Необходимо задать характеристики всех трёх переменных project→adjective editor. Выбираем переменную prohod в окне «Adjectives for variables», нажимаем Edit. Здесь каждой входной и выходной переменной ставим в соответствие набор функций принадлежности Adjective→Change List→New. В появившемся окне «Create Adjective(s)» задаём параметры: количество функций принадлежности (Number) равное 3; вид функции принадлежности (Shape) – Triangle; ширина основания (base width) равная 60000.0 (рис.5).
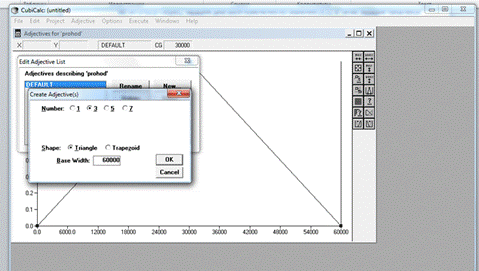
Рис.5
В окне «Edit Adjective List» присвоим наименования – small, middle, big соответственно большой, средней и маленькой проходимости (рис.6).
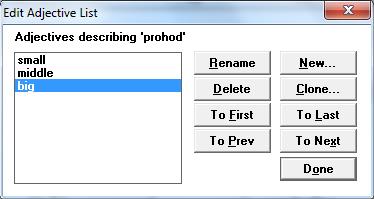
Рис.6
Аналогично для переменной rast (рис.7):
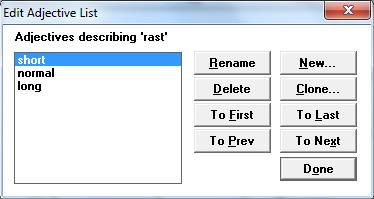
Рис.7
Получаем следующие функции принадлежности (рис.8):
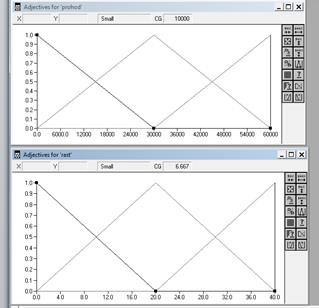
Рис.8
Определение набора правил, связывающих входные переменные с выходными
Необходимо определить набор правил, которые связывают входные переменные с выходными. Для этого в редакторе правил вывода Project→Rules определяем (рис.9):
IF prohod is big AND rast is normal THEN rate is good;
IF prohod is small AND rast is normal THEN rate is bad;
IF prohod is middle AND rast is long THEN rate is normal;
IF prohod is middle AND rast is normal THEN rate is normal;
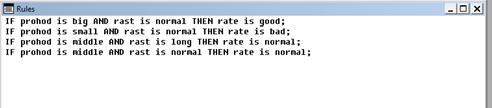
Рис.9
Настройка входного файла
Для присоединения входного файла к проекту, необходимо создать файл с расширением .txt, задать имя файла (File→Input File) и некоторые его атрибуты (рис.10):
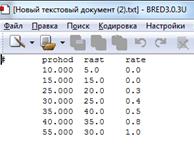
Рис.10
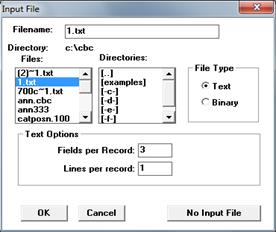
Рис.10
Проверка работы системы
Для проверки работы системы необходимо запустить сценарий Execute→Run. Появится окно, содержащее значения переменных. Через некоторое время CubiCalc дойдёт до конца входного файла и появится итоговое сообщение (рис.11):
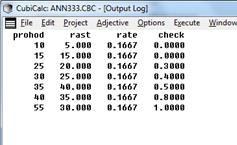
Рис.11
Заключение
После применения на практике знаний, полученных в процессе изучения курса «Проектирование баз данных и баз знаний», и приобретения практических навыков при проектировании и создании нечёткой экспертной системы в программном пакете CubiCalc можно выделить отличительные особенности данных систем:
· Возможность оперировать входными данными, заданными нечётко;
· Возможность нечёткой формализации критериев оценки и сравнения;
· Возможность проведения качественных оценок, как входных данных, так и выводимых результатов;
· Возможность проведения быстрого моделирования сложных динамических систем и их сравнительный анализ с заданной степенью точности;
В отличие от традиционной математики, требующей на каждом шаге моделирования точных и однозначных формулировок закономерностей, нечёткая логика предлагает совершенно иной уровень мышления, благодаря которому творческий процесс моделирования происходит на наивысшем уровне абстракции, при котором постулируется лишь минимальный набор закономерностей.
Таким образом, нечёткая логика в некоторых случаях позволяет улучшить качество управления объектами. Решающую роль в оптимизации показателей эффективности играют эксперты, которые определяют количество выходных и входных переменных, число термов для каждой переменной, виды функций принадлежности, т. к. изменение этих параметров приводит к улучшению или ухудшению процесса управления объектом.
Однако, я считаю, что важнейшим недостатком нечёткой логики является отсутствие единого метода моделирования систем, т. е. для каждого случая приходится заново проектировать нечёткую подпрограмму, определяя шаг за шагом все параметры и строя свою таблицу решений.