Всякая сложная логическая функция может быть сведена к ДНФ

Комбинационные схемы. Основы синтеза КС.

Методы минимизации логических функций.

Техническим аналогом переключательной (булевой) функции является схема, выполняющая соответствующие этой функции логические преобразования информации.

Все вентили, входящие в состав переключательной схемы, обладают характерной особенностью:

Сигналы на выходах этих логических элементов полностью определяются входными сигналами, т.е. сигналами, присутствующими в рассматриваемый момент времени на их входах. От сигналов, подаваемых на входы в более ранние моменты времени, выходные сигналы не зависят.

Поэтому и сами вентили, и построенные на их основе схемы, относят к классу комбинационных схем, т.е. схем, не обладающих памятью.

Комбинационной называется такая схема, в которой выходные сигналы определяются текущими входными сигналами.

Не все схемы обладают таким свойством. Например, схема, содержащая элементы памяти, может сгенерировать выходные сигналы, которые зависят от значений, хранящихся в памяти.

С помощью КС в CPU реализуются все основные логические и арифметические операции. Например, вентиль, реализующий функцию ИСКЛЮЧАЮЩЕЕ ИЛИ, является базой для построения всех суммирующих схем.

Итак, любая КС является синтезом вентилей – простейших логических элементов, реализующих основные булевы функции. Следовательно, свойства КС полностью определяет таблица истинности соответствующей логической функции. Можно сказать, что КС фактически реализует таблицу истинности. Число аргументов функции – это набор входных сигналов реализуемой схемы. Значение функции на конкретном наборе аргументов в таблице – это указание на то, какой сигнал должен быть на выходе схемы при определенной комбинации сигналов на входах.

Перед нами стоит задача синтезировать КС, имея таблицу истинности соответствующей ей логической функции. Т.е., мы знаем, как должна вести себя схема при том или ином наборе входных сигналов. Какие же вентили, и в какой комбинации мы должны использовать для построения схемы? Для этого мы должны получить аналитическую запись логической функции, которая задана нам табличным способом. Эта аналитическая запись может оказаться достаточно громоздкой, соответственно ее схемная реализация получится отягощенной большим количеством вентилей. Разработчики схем стараются сократить число вентилей, чтобы снизить цену, уменьшить занимаемое схемой место, сократить потребление энергии и т.д. Чтобы упростить схему, разработчик должен найти другую схему, которая может выполнять ту же функцию, но при этом требует меньшего количества вентилей. Булева алгебра является ценным инструментов в поиске эквивалентных схем.

Синтез произвольной КС по заданной таблице истинности заключается в получении формульной, т.е. аналитической записи соответствующей логической функции, в упрощении (минимизации) полученной логической формулы и, наконец, в составлении искомой схемы по упрощенной формуле.

Для того чтобы от табличного задания функции перейти к ее аналитическому представлению, мы должны определить ряд понятий.

Одна и та же функция может быть задана множеством различных формул. Поэтому функции трудно сравнивать. Канонические формы - это запись функции по единым правилам.

Наборы, на которых задана функция, могут быть представлены в виде конституэнтов(простых конъюнкций).

Конституэнтом (простой конъюнкцией) называется логическое произведение всех без исключения аргументов функции, в котором аргументы, равные 0, берутся со знаком инверсии, а равные 1, без него.

При числе аргументов n число простых конъюнкций равно 2ⁿ. Например, конституэнту 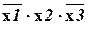соответствует двоичный набор 010, а конституэнту 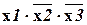- набор 100.

Для представления логических функций существуют две формы:

· дизъюнктивная нормальная форма (ДНФ);

· конъюнктивная нормальная форма (КНФ).

Дизъюнктивная нормальная форма (ДНФ) – это сумма произведений, образованных из переменных и их отрицаний. ДНФ не содержит скобок.

Например, формы 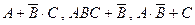- дизъюнктивные нормальные формы, а 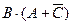- нет. (Сначала выполняется конъюнкция, а затем дизъюнкция.)

Конъюнктивная нормальная форма (КНФ) – это произведение сумм, состоящих из переменных и их отрицаний.

Например, 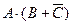. (Сначала выполняется дизъюнкция, а затем конъюнкция.)

Теорема о ДНФ.

Всякая сложная логическая функция может быть сведена к ДНФ.

Для того, чтобы сделать это необходимо:

• записать булеву функцию в виде {+, × , -};
• с помощью законов де Моргана спустить отрицание до отдельных переменных и уничтожить двойные отрицания (закон двойного отрицания);
• с помощью закона дистрибутивности уничтожить все произведения сумм и провести поглощение.

Полученная форма удовлетворяет определению ДНФ.

Если ДНФ функции f1(x₁, x₂, …, x_n) от n переменных в каждой своей конъюнкции содержит все n переменных либо их отрицания, то это совершенная дизъюнктивная нормальная форма (СДНФ).Т.е. это такая ДНФ, в которой все входящие конъюнкции имеют ранг n.

Каждая функция имеет одну единственную СДНФ, и она может быть получена из таблицы истинности этой функции путем записи через знак логического сложения всех простых конъюнкций, на которых эта функция определена как истинная.

Конъюнкции, составляющие СДНФ и соответствующие тем наборам, для которых функция принимает единичные значения, называют минтермом.

Например, для функции, заданной следующей таблицей истинности:

х1	х2	х3	f(x1,x2,x3)

СДНФ будет следующей:

СДНФ(f1) = 000 + 010 + 100 + 101 + 110 = =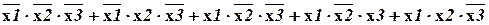

Обратите внимание: для константы 0 не существует СДНФ, т.к. нет ни одного набора переменных на котором она была бы определена как истинная!

Теорема о КНФ.