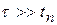Дифференцирующая (укорачивающая) и разделительная RC-цепи
Дифференцирующей цепью называют такую цепь, сигнал на выходе которой имеет значения, пропорциональные в каждый момент производной от входного сигнала. Следовательно, 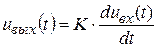 . Коэффициент К должен выражаться в секундах, в противном случае размерность левой и правой частей равенства не будет одинакова. Идеальным дифференцирующим устройством можно считать конденсатор С или катушку L. Например, при использовании конденсатора С можно считать входным сигналом напряжение на нём
. Коэффициент К должен выражаться в секундах, в противном случае размерность левой и правой частей равенства не будет одинакова. Идеальным дифференцирующим устройством можно считать конденсатор С или катушку L. Например, при использовании конденсатора С можно считать входным сигналом напряжение на нём 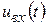 , а выходным — ток
, а выходным — ток 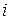 в цепи. Эти переменные связаны известным соотношением
в цепи. Эти переменные связаны известным соотношением 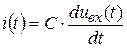 , т.е. ток в цепи пропорционален производной от входного напряжения. Однако использовать эту схему для практических целей нельзя, так как она не содержит элемента, который обеспечивал бы какую-либо регистрацию значений тока, измерение его значений.
, т.е. ток в цепи пропорционален производной от входного напряжения. Однако использовать эту схему для практических целей нельзя, так как она не содержит элемента, который обеспечивал бы какую-либо регистрацию значений тока, измерение его значений.
Для того чтобы получить выходной сигнал в форме, удобной для наблюдения или регистрации, в цепь последовательно включают токочувствительный прибор с внутренним сопротивлением R. В простейшем случаи это может быть резистор R, напряжение на котором пропорционально току 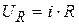 .
.
Рассмотренная RC-цепочка может выполнять функции как дифференцирующей (укорачивающей) при 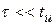 , так и разделительной цепи, если
, так и разделительной цепи, если 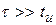 .
.
На рис.1.11 показаны графики напряжений 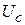 и
и 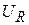 такой цепочки.
такой цепочки.

а) б)
Рисунок 1.11 — а) режим 1 – 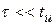 , б) режим 2 –
, б) режим 2 – 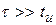
Рассмотрим два режима:
I. Дифференцирующая цепь — 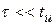 , при этом возможны два варианта: а)
, при этом возможны два варианта: а) 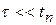 ; б)
; б) 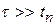 ;
;
II. Разделительная цепь — 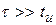 , при этом также: а)
, при этом также: а) 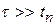 ; б)
; б) 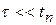 .
.
I. Рассмотрим дифференцирующую цепочку под воздействием импульсной последовательности (рис.1.12).

Рисунок 1.12 — Принципиальная схема укорачивающей RC-цепочки
При импульсе конденсатор С заряжается под воздействием зарядного тока 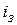 , при паузе — разряжается, обуславливая разрядный ток
, при паузе — разряжается, обуславливая разрядный ток 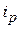 . При этом
. При этом 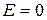 .
.
Допустим 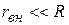 ,тогда им можно пренебречь (
,тогда им можно пренебречь ( 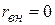 ).
).
Рассмотрим режим I, вариант а): 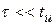 ,
, 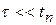 .
.
После окончания импульса (момент времени 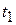 )
) 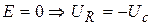 .
.
В период паузы ( 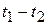 ) разряд конденсатора С получается полный (см. рис.1.13.), т.к.
) разряд конденсатора С получается полный (см. рис.1.13.), т.к. 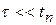 ;
;
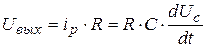 ;
;
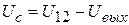 .
.
Тогда
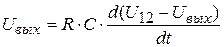 ;
;
При 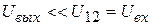 получим:
получим:
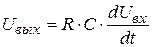 .
.
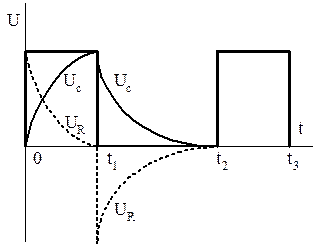
Рисунок 1.13 — Зависимости 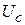 (t) и
(t) и 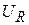 (t)
(t)
Значит, получена идеальная дифференцирующая цепь. Следовательно, для того чтобы цепь была дифференцирующей необходимо выполнение трёх условий:
1) 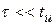 ;
;
2) 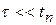 ;
;
3) 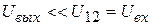 ;
;
При этом график напряжения 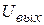 при наличии импульсной последовательности на входе будет иметь следующий вид (рис.1.14):
при наличии импульсной последовательности на входе будет иметь следующий вид (рис.1.14):
Режим I, вариант б): 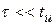 ,
, 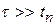 :
:
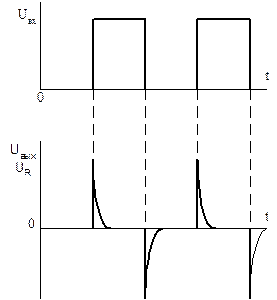
Рисунок 1.14 — График напряжения 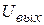 дифференцирующей цепи при наличии импульсной последовательности на входе
дифференцирующей цепи при наличии импульсной последовательности на входе
Графики напряжений 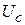 и
и 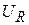 приведены на рис.1.15. В этом режиме с момента времени
приведены на рис.1.15. В этом режиме с момента времени 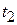 имеют место, в отличие от варианта а), новые начальные условия
имеют место, в отличие от варианта а), новые начальные условия 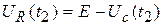 . Такой режим называют режимом негармонических возмущений.
. Такой режим называют режимом негармонических возмущений.
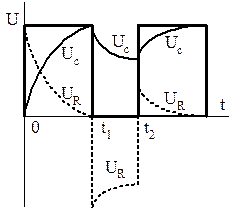
Рисунок 1.15 — Зависимости 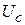 (t) и
(t) и 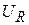 (t); режим I, вариант б):
(t); режим I, вариант б): 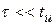 ,
, 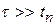
В период импульса переходные процессы аналогичны рассмотренным в варианте а), а в период паузы конденсатор С не успевает разрядиться до нуля за время 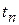 , поэтому нулевые начальные условия не выполняются и для дифференцирующей цепочки такой вариант неприемлем.
, поэтому нулевые начальные условия не выполняются и для дифференцирующей цепочки такой вариант неприемлем.
Режим II при 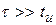 ,
, 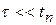 обеспечивает вариант разделительной цепочки.
обеспечивает вариант разделительной цепочки.
В момент времени 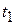 , после действия импульса, (см. рис.1.16)
, после действия импульса, (см. рис.1.16) 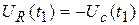 , а в момент времени
, а в момент времени 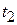 имеют место нулевые начальные условия. Сигнал на выходе повторяет сигнал на входе. Следовательно, такая цепочка является разделительной.
имеют место нулевые начальные условия. Сигнал на выходе повторяет сигнал на входе. Следовательно, такая цепочка является разделительной.

Рисунок 1.16 — Зависимости 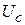 (t) и
(t) и 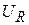 (t); режим II при
(t); режим II при 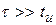 ,
, 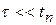
Режим II, при 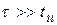 ,
, 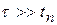 , аналогичен варианту б) режима I, поскольку в момент времени
, аналогичен варианту б) режима I, поскольку в момент времени 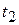 также имеют место новые, ненулевые начальные условия (рис.1.17) (режим негармонических возмущений). Для разделительной цепи такой вариант неприемлем.
также имеют место новые, ненулевые начальные условия (рис.1.17) (режим негармонических возмущений). Для разделительной цепи такой вариант неприемлем.
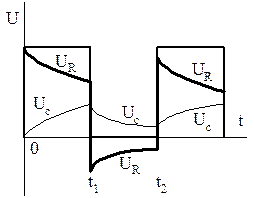
Рисунок 1.17 — Зависимости 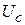 (t) и
(t) и 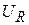 (t); режим II при
(t); режим II при 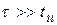 ,
,