Табличное построение логики высказываний

Логика высказываний — раздел символической логики, поэтому в ней используется язык символов. Символы этого языка:

а) p, q, r, s, p₁,q₁,... — пропозициональные символы (пропозициональные переменные);

б) Ø, Ù, Ú, É, º — логические термины (логические константы);

в) (,) — скобки.

Определение формулы:

а) пропозициональная переменная есть формула;

б) если А есть формула и В есть формула, то ØA, (А Ù В),(A Ú B), (А É В), (А º В) — формулы;

в) ничто иное не есть формула.

Согласно определению, выражения (рÙq), ((рÙØq) º (р É r)), ØØ p, r являются формулами, а выражения (p Ú q) É, r º, Ù (р É s) — нет.

Примем соглашения об опускании скобок в формулах. Будем опускать внешние скобки. Условимся считать, что знак Ø связывает теснее, чем знаки Ù, Ú, É, º; знак Ù — теснее, чем Ú, É, º; Ú — теснее, чем É, º; É теснее, чем º. Исходя из сказанного, в формулах ((рÙØq) É (rÚs)), (ØØр º (р É q)) можно опустить скобки следующим образом:

р ÙØ q É r Ú s, ØØ р º (р É q).

Упражнение 4

Восстановите скобки в следующих формулах:

1. р Ù q É r;

2. Ø q É ( p ÚØ r) Ù q;

3. р É q º р ÙØ r É р Ú q;

4. р Ù q É r º р É (q É r).

При табличном построении логики высказываний логические константы определяются посредством таблиц истинности. При этом принимается, что каждое высказывание имеет одно значение — или “истина”, или “ложь”.

Приведем эти табличные определения логических констант еще раз:

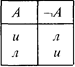А	В	А Ù В	A Ú В	А É В	А º В
и	и	и	и	и	и
и	л	л	и	л	л
л	и	л	и	и	л
л	л	л	л	и	и

Назовем формулу, являющуюся пропозициональной переменной, элементарной, формулу, содержащую логические константы, — сложной. В сложной формуле можно выделить логическую константу, называемую главной логической константой формулы. Поясним, как это можно сделать.

Каждую сложную формулу логики высказываний можно единственным образом представить в виде Ø А, или А Ù В, или A Ú В, А É В или А º В. Буквами А и В здесь обозначаются формулы, являющиеся частями сложной формулы. Подформулы, конечно, в свою очередь могут быть сложными формулами.

Представив таким образом сложную формулу, мы выделяем в ней последнюю по построению логическую константу, которая и называется главной логической константой формулы.

Найдем главную логическую константу формулы Ø p Ú q É p ÙØ q.

Восстановим скобки в этой формуле:

((Ø p Ú q) É (р ÙØ q)).

Эту формулу единственным образом можно представить в форме А É В. Ее главным знаком является знак импликации. Можно представить в виде “дерева” процесс построения этой формулы:

р				q
i				^
^р		<l	Р
1^		^	^	^
Ьр	V			(pn^q)
	2			4
	^			i

p q

↓ ↓

Ø p q p Ø q

1↓ ↓ ↓ 3↓

(Ø p Ú q) (p ÙØq)

2 4

↓ ↓

((Ø p Ú q)É(p ÙØq))

5

Стрелки показывают, что из формул (или формулы), от которых они направлены, образована формула, к которой они направлены. Цифры под логическими константами указывают порядковый номер константы по построению формулы. Последняя по построению константа имеет номер 5.

Упражнение 5

Найдите главную логическую константу в каждой из следующих формул.

1. (р Ú q) Ù r É рÙ r;

2. р ÙØ q É rº рÉ (Ø qÉ r);

3. ((pÉ q) É q) É q;

4. Ø (ØрÚ р ).

Построим таблицу истинности для формулы рÚ q ÉØ q. В таблице под главной константой формулы будем писать истинностные значения формулы в целом. В этой формуле главной логической константой является знак импликации. Чтобы установить истинностные значения всей формулы, необходимо установить истинностные значения подформул, составляющих ее, т.е. формул рÚ q и Ø q. Истинностные значения этих формул будем соответственно писать под логическими константами Ú и Ø. В результате получим таблицу истинности:

p	q	рÚ q ÉØ q
и	и	и л л
и	л	и и и
л	и	и л л
л	л	л и и

Проанализируем первую строку таблицы. В первой строке пропозициональные переменные р и q имеют значение и. Чтобы установить истинностное значение формулы в целом, следует установить истинностные значения подформул рÚ q и Ø q . При значении и переменных р и q рÚ q имеет значение и, при значении и переменной q формула Ø q имеет значение л, что видно из таблиц истинности для дизъюнкции и отрицания, приведенных выше.

p	q	рÚ q ÉØ q
и	и	и л

Оказывается, антецедент формулы в целом, являющейся импликацией, имеет значение и, а консеквент — л. В приведенной выше таблице для импликации в этом случае импликация имеет значение л:

p	q	рÚ q ÉØ q
и	и	и л л

Можно упростить построение таблиц истинности, если значения пропозициональных переменных писать под переменными, входящими в саму формулу.

В приведенном выше табличном определении отрицания всего две строки, а в определениях для конъюнкции, дизъюнкции, импликации и эквивалентности — по четыре строки. Как установить число строк в таблице в общем случае, т.е. как установить, сколько может быть различных возможных наборов значений переменных, входящих в формулу?

Число строк в таблице истинности определяется по следующей формуле: число строк таблицы = 2ⁿ, где п — число различных пропозициональных переменных, входящих в формулу, а число 2 показывает число истинностных значений (и, л).

Учитывая сказанное, построим таблицу истинности для формулы:

(р É (q É r)) É ((р É q) É (р É r)).

Формула содержит три различные переменные. Следовательно, число строк в таблице = 2ⁿ, 2³=8. Разделим число строк пополам и напишем под первой пропозициональной переменной (первой слева) в столбик четыре раза и и четыре раза л:

(р É (q É r)) É ((р É q) É (р É r)).

и

и

и

и

л

л

л

л

Каждую половину всех строк, т.е. в данном случае каждые четыре строки, в свою очередь разделим пополам и напишем под второй по вхождению слева пропозициональной переменной, отличной от первой пропозициональной переменной, в обеих половинах строк два раза и и два раза л:

(р É (q É r)) É ((р É q) É (р É r)).

и и

и ___и_______________________

и л

и___ л_______________________

л и

л ___и________________________

л л

л л

Разделим, далее, половину каждой половины пополам и под третьей по вхождению слева переменной, отличной от первых двух переменных, напишем и, если эта часть (строка) нечетная при пересчете сверху вниз, или л, если часть (строка) четная:

и

(р É ( q É r)) É ((р É q) É (р É r)).

и и __и_____________________

и____и__ л_____________________

и

и л ___и_____________________

и____л__ л_____________________

л и __и_____________________

л____и___л_____________________

л л___и_____________________

л л л

Деление производится до тех пор, пока полученная в результате деления часть не будет состоять из одной строки.

Одна и та же переменная может входить в формулу несколько раз. В одной и той же строке под всеми вхождениями одной и той же переменной пишется одно и то же значение, т.е. для завершения построения таблицы истинности следует под каждым вторым (третьим и т.д.) вхождением переменной написать те же значения, что и под первым вхождением этой переменной.

(р É (q É r)) É((р É q) É(р É r)).

и и___и___и___и___и___и

и___и___л___и___и___и___л

и л___и___и___л___и___и

и___л___л___и___л___и___л

л и___и___л___и___л___и

л___и___л___л___и___л___л

л л___и___л___л___л___и

л л л л л л л

Несложно завершить построение таблицы истинности:

(р É (q É r)) É ((р É q) É (р É r)).

и и и и и и__и_и_и_и__и_и_и

и л и__л_л__и__и_и_и_л__и_л_л

и и л и и и__и_л_л_и__и_и_и

и_и__л__и_л__и__и_л_л_и__и_л_л

л и и и и и__л_и_и_и__л_и_и

л и и__л_л__и__л_и_и_и__л_и_л

л и л и и и__л_и_л_и__л_и_и

л и л и л и л и л и л и л

Эта формула имеет значение “истина” при каждом наборе значений входящих в нее переменных.

Формула, принимающая значение “истина” при любом наборе значений входящих в нее переменных, называется тождественно-истинной, или законом логики, или общезначимой.

Формула, принимающая значение “ложь” при любом наборе значений входящих в нее переменных, называется тождественно-ложной, или противоречием.

Формула, принимающая значение “истина” хотя бы при некоторых наборах значений переменных, называется выполнимой.

Упражнение 6

Установите, какие из следующих формул являются тождественно-истинными, какие — тождественно-ложными и какие — выполнимыми.

1.р É р.

2. Ø (р Ù q É р).

3. (р É q Ù r) É (p Ú r É q).

4. р Ù (q Ú r) º (р Ù q) Ú (р Ú r).

5. ((р ÉØ q) ÉØ р).

Логика высказываний, построенная табличным способом, дает эффективную процедуру для выявления законов логики, а также метод проверки правильности рассуждении. Рассуждение считается правильным, если между его посылками и заключением имеет место отношение логического следования. Определяем последнее: из посылок Г следует заключение В, если импликация, имеющая антецедентом конъюнкцию формул, соответствующих посылкам, а консеквентом — формулу, соответствующую заключению, является тождественно-истинной.

Пусть дано рассуждение: “Если Иванов является участником этого преступления, то он знал потерпевшего. Иванов не знал потерпевшего, но знал его жену. Потерпевший знал Иванова. Следовательно, Иванов является участником этого преступления”. Для определения правильности рассуждения требуется:

во-первых, обозначить различными символами различные простые высказывания, входящие в рассуждение. В приведенном рассуждении встречаются следующие простые высказывания: “Иванов является участником этого преступления”, “Иванов знал потерпевшего”, “Иванов знал жену потерпевшего”. “Потерпевший знал Иванова”. Обозначим их соответственно символами p,q, r, s;

во-вторых, перевести на язык логики высказываний посылки и заключение. Переводом посылок являются формулы р É q, Ø q Ù r, s, а переводом заключения — формула р (союз “но” соответствует в данном случае союзу “и”);

в-третьих, формулы, являющиеся переводом посылок, последовательно соединить знаком конъюнкции. Получаем формулу:

((p É q) Ù (Ø q Ù r )) Ù s;

в-четвертых, к полученной формуле присоединить справа знаком импликации формулу, являющуюся переводом заключения. Получаем формулу:

((р É q) Ù (Ø q Ù r)) Ù s É р;

в-пятых, для полученной формулы построить таблицу истинности.

Если формула, являющаяся переводом рассуждения на язык символов, оказывается тождественно-истинной, то можно сделать вывод о том, что рассуждение правильное, если тождественно-ложной, то рассуждение неправильное. Может оказаться, что формула является выполнимой, но не тождественно-истинной. В том случае нет оснований считать рассуждение правильным. Необходимо продолжить анализ рассуждения, но уже средствами более богатого раздела логики — средствами логики предикатов.

Вернемся к рассматриваемому рассуждению. Построим таблицу истинности для формулы, являющейся переводом этого рассуждения на язык символов:

((р É q) Ù (Ø q Ù r)) Ù s É р

и и и л л и л и л и и и

и и и л л и л и л л и и

и и и л л и л л л и и и

и и и л л и л л л л и и

и л л л и л и и л и и и

и л л л и л и и л л и и

и л л л и л л л л и и и

и л л л и л л л л л и и

л и и л л и л и л и и л

л и и л л и л и л л и л

л и и л л и л л л и и л

л и и л л и л л л л и л

л и л и и л и и и и л л

л и л и и л и и л л и л

л и л л и л л л л и и л

л и л л и л л л л л и л .

Формула является выполнимой, но не общезначимой. Следовательно, нет оснований считать рассматриваемое рассуждение правильным.

Если формула содержит много переменных, то в некоторых случаях можно не строить таблицу, а путем особых “сокращающих” рассуждений установить, является ли она общезначимой, противоречивой или же выполнимой, но не общезначимой.

Рассмотрим проанализированную выше формулу. Предположим, что при некотором наборе значений переменных она принимает значение “л”:

((p É q) Ù (Ø q Ù r)) Ù s É p

Это возможно, если значение консеквента — “л”, а антецедента — “и”, а следовательно, каждого члена конъюнкции — “и”:

((p É q) Ù (Ø q Ù r)) Ù s É p

и и и л л

Поскольку переменной р уже приписано значение “л”, пишем “л” под первым вхождением р в формулу:

((p É q) Ù (Ø q Ù r)) Ù s É p

л и и и л л

Подформула Ø q Ù r имеет значение “и”, если, и только если, Ø q и r имеют значение “и”:

((p É q) Ù (Ø q Ù r)) Ù s É p

л и и и и и л л

Поскольку подформула Ø q имеет значение “и”, под q пишем “л”:

((p É q) Ù (Ø q Ù r)) Ù s É p

л и и л и и и л л

Тогда

((p É q) Ù (Ø q Ù r)) Ù s É p

л и л и и л и и и и л л

Формула принимает значения “л” при значениях “л”, “л”, “и”, “и” соответственно переменных р, q, r и s.

Очевидно, что при значении “и” переменной эта формула принимает значение “и”. Формула принимает как значение “л”, так и значение “и”, а следовательно, является выполнимой, но не общезначимой.

Рассмотрим формулу:

((p É q) Ù ( q É r)) Ù p É r

Чтобы доказать, что формула является общезначимой, будем рассуждать от противного. Предположим, что она не общезначима, т.е. при некотором наборе значений переменных принимает значение “л”. Это возможно, если ее антецедент, а следовательно, каждый член конъюнкции принимает значение “и”:

((p É q) Ù ( q É r)) Ù p É r

и и и и и л л

((p É q) Ù ( q É r)) Ù p É r

и и и и л и л и и л л

Приходим к противоречию, так как в этом случае, чтобы антецедент импликации оставался истинным, первому вхождению переменной q следует приписать значение “и”, а второму — “л”. Следовательно, формула является общезначимой.

Упражнение 7

Являются ли правильными следующие рассуждения?

1. Если философ — дуалист, то он не материалист. Если он не материалист, то он диалектик или метафизик. Он не метафизик. Следовательно, он диалектик или дуалист.

2. Если это преступление совершил Иванов, то он знает, где находятся похищенные деньги. Иванов не знает, где находятся похищенные деньги, но знает, где находятся похищенные вещи. Иванова видели на месте преступления примерно в то время, когда преступление было совершено. Следовательно, Иванов не совершал этого преступления.

3. Если данное явление психическое, то оно обусловлено внешним воздействием на организм. Если оно физиологическое, то оно тоже обусловлено внешним воздействием на организм. Данное явление не психическое и не физиологическое. Следовательно, оно не обусловлено внешним воздействием на организм.

4. Если человек принял какое-то решение и он правильно воспитан, то он преодолеет все конкурирующие желания. Человек принял решение, но не преодолел некоторых конкурирующих желаний. Следовательно, он неправильно воспитан.

5. “Если Джонс не встречал этой ночью Смита, то либо Смит был убийцей, либо Джонс лжет. Если Смит не был убийцей, то Джонс не встречал Смита этой ночью, и убийство имело место после полуночи. Если убийство имело место после полуночи, то либо Смит был убийцей, либо Джонс лжет. Следовательно, Смит был убийцей.” (Мендельсон Э. Введение в математическую логику. М., 1971. С. 31)

6. “Если капиталовложения останутся постоянными, то возрастут правительственные расходы или возникнет безработица. Если правительственные расходы не возрастут, то налоги будут снижены. Если налоги будут снижены и капиталовложения останутся постоянными, то безработица не возрастет. Следовательно, правительственные расходы возрастут.” (Мендельсон Э. Введение в математическую логику. М., 1971. С. 31)

Упражнение 8

Осуществите обоснование приведенных выше правильных модусов умозаключений посредством таблиц истинности.

Еще один способ установления отношения логического следования между суждениями, а также и других отношений, заключается в следующем:

суждения переводятся на язык логики высказываний;

для формул, соответствующих суждениям, строятся сравнимые таблицы истинности;

устанавливаются виды отношений между суждениями на основе следующих определений:

1) суждения совместимы по истинности, если и только если в сравнимых таблицах есть строка, в которой все формулы имеют значение “истина”;

2) суждения совместимы по ложности, если и только если в сравнимых таблицах есть строка, в которой все формулы имеют значение “ложь”;

3) из суждений А₁, А₂ , ..., A_n следует суждение В, если и только если в сравнимых таблицах нет строки, в которой все формулы, соответствующие суждениям А₁, А₂ , ..., A_n, имеют значение “истина”, а формула, соответствующая суждению В, имеет значение “ложь”.

Остальные отношения являются производными по отношению к названным.

Пример: Пусть переводами трех суждений являются, соответственно, формулы Ø r Ù р, p É q Ú r, q. Построим для этих формул таблицы истинности таким образом, чтобы эти таблицы можно было сравнивать. Для этого выпишем вначале все переменные, входящие в какие-либо из этих формул. Это переменные р, q, r . Число строк таблиц = 2³ = 8. Строим таблицы:

Между первыми двумя суждениями и последним имеет место отношение логического следования. Эти суждения (все три) совместимы по истинности (см. строку 5) и не совместимы по ложности.

Упражнение 9

Описанным способом установите отношения между суждениями пунктов 1, 3, 4, 5 упражнения 10 § 3 гл. IV.

Упражнение 10

Установите отношения между суждениями “Если философ является дуалистом, то он не идеалист”, “Если философ не идеалист, то он диалектик или метафизик”, “Этот философ не метафизик”, “Он диалектик или не дуалист”.